Thấu kính

Nhận xét: thấu kính cho ảnh thật → ảnh ngược chiều với vật (k < 0), ở khác phía thấu kính so với vật

Số phóng đại của ảnh là:

\(k =  - \dfrac{{d'}}{d} \Rightarrow  - \dfrac{{d'}}{{20}} =  - 5 \Rightarrow d' = 100\,\,\left( {cm} \right)\)

Khoảng cách giữa vật và ảnh là:

\(L = d + d' = 20 + 100 = 120\,\,\left( {cm} \right)\)

+ Gọi k là số phóng đại ảnh của thấu kính; \({S_v} = {\rm{ }}a{\rm{ }}x{\rm{ }}b\) là diện tích vật; \({S_a} = {\rm{ }}a'{\rm{ }}x{\rm{ }}b'\)  là diện tích ảnh trên màn.

+ Theo định nghĩa: \(a'{\rm{ }} = {\rm{ }}\left| k \right|a;{\rm{ }}b'{\rm{ }} = {\rm{ }}\left| k \right|b\)

\( \to {S_a} = {k^2}\left( {a{\rm{ }}x{\rm{ }}b} \right) = {k^2}{S_v} \to \left| k \right| = \sqrt {\frac{{{S_a}}}{{{S_v}}}} \)

+ Thay số, lưu ý ảnh thật ngược chiều với vật, ta được k = - 20.

+ Vận dụng công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\) và \(k =  - \frac{{d'}}{d}\)

\( \to d = \frac{{f\left( {k - 1} \right)}}{k}\)

Thay số, được d = 10,5 cm; d' = 210 cm

+ Thấu kính phân kỳ tạo ảnh ảo của đèn, ảnh này gần thấu kính hơn đèn.

+ Ánh sáng từ đèn truyền qua thấu kính đến màn coi như phát ra từ ảnh của đèn tạo bởi thấu kính.

+ Đường truyền ánh sáng đến màn được thể hiện như hình vẽ.

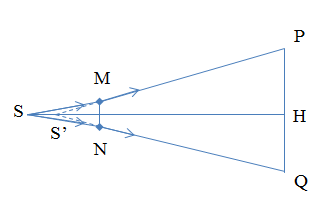
+ Ta có tam giác S'MN đồng dạng với tam giác S'PQ:

\(\frac{{MN}}{{PQ}} = \frac{{|d'| + OH}}{{|d'|}}\)

Thay số, ta được:

 \(OH{\rm{ }} = {\rm{ }}20\left| {d'} \right|\) (1)

+ Theo công thức xác định vị trí ảnh:

\(d' = \frac{{df}}{{d - f}} = \frac{{3.( - 5)}}{{3 + 5}} =  - \frac{{15}}{8}cm\) (2)

Từ (1) và (2), ta được: \(OH{\rm{ }} = {\rm{ }}37,5{\rm{ }}cm\)