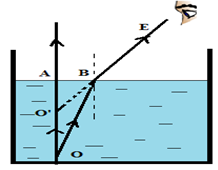
Bể chứa nước có thành cao 80cm và đáy phẳng dài 120cm. Độ cao mực nước trong bể là 60cm, chiết suất của nước là 4/3. Ánh nắng chiếu theo phương nghiêng một góc 300 so với phương ngang. Độ dài của bóng đen tạo thành trên mặt nước là:
Ta có, ánh nắng chiếu nghiêng một góc 300 so với phương ngang => i = 600
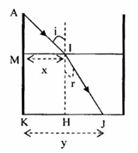
Từ hình vẽ ta có:
\(\tan i = \frac{x}{{MA}} \to x = MAtan60 = 20\sqrt 3 cm\)
=> Độ dài bóng đen tạo trên mặt nước là \(x = 20\sqrt 3 cm\)
Bể chứa nước có thành cao 80cm và đáy phẳng dài 120cm. Độ cao mực nước trong bể là 60cm, chiết suất của nước là 4/3. Ánh nắng chiếu theo phương nghiêng một góc 300 so với phương ngang. Độ dài của bóng đen tạo thành dưới đáy bể là:
Ta có, ánh nắng chiếu nghiêng một góc 300 so với phương ngang => i = 600
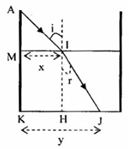
Từ hình vẽ ta có:
\(\tan i = \frac{x}{{MA}} \to x = MAtan60 = 20\sqrt 3 cm\)
\({\mathop{\rm s}\nolimits} {\rm{inr}} = \frac{{HJ}}{{\sqrt {H{I^2} + H{J^2}} }}\)
+ Theo định luật khúc xạ ánh sáng, ta có:
\(\begin{array}{l}\frac{{\sin i}}{{{\mathop{\rm s}\nolimits} {\rm{inr}}}} = n \leftrightarrow \frac{{\sin {{60}^0}}}{{\frac{{HJ}}{{\sqrt {H{I^2} + H{J^2}} }}}} = \frac{4}{3} \to \frac{{HJ}}{{\sqrt {H{I^2} + H{J^2}} }} = \frac{{3\sqrt 3 }}{8}\\ \leftrightarrow \frac{{H{J^2}}}{{H{I^2} + H{J^2}}} = \frac{{27}}{{64}} \to H{J^2} = \frac{{27}}{{37}}H{I^2} \to HJ = \sqrt {\frac{{27}}{{37}}} .60 = 51,25cm\end{array}\)
Vậy vệt sáng ở dưới đáy bể là: \(y = x + HJ = 20\sqrt 3 + 51,25 = 85,9cm\)
Mắt người và cá cùng cách mặt nước là 60cm, cùng nằm trên một mặt phẳng vuông góc với mặt nước. Biết chiết suất của nước là n = 4/3. Hỏi người thấy cá cách mình bao xa?
Khi người nhìn thấy cá thì tia sáng từ cá đến mắt người (hình vẽ)
+ Vì mắt nhìn xuống đáy chậu gần vuông góc nên góc r rất nhỏ
=> i cũng rất nhỏ
+ Gọi A là cá thật và A’ là ảnh của cá
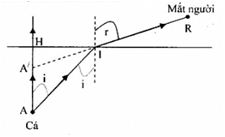
Từ hình vẽ, ta có: \(\left\{ \begin{array}{l}\tan i = \frac{{HI}}{{HA}} \approx \sin i \approx i\\{\mathop{\rm t}\nolimits} {\rm{anr}} = \frac{{HI}}{{HA'}} \approx {\mathop{\rm s}\nolimits} {\rm{inr}} \approx {\rm{r}}\end{array} \right.\)
Theo định luật khúc xạ ánh sáng, ta có:
\(n\sin i = {\mathop{\rm s}\nolimits} {\rm{inr}} \to \frac{{\sin i}}{{{\mathop{\rm s}\nolimits} {\rm{inr}}}} = \frac{1}{n} \leftrightarrow \frac{{HA'}}{{HA}} = \frac{1}{n} \to HA' = \frac{{HA}}{n} = \frac{{60}}{{\frac{4}{3}}} = 45cm\)
=> Người nhìn thấy cá cách mắt mình đoạn 60 + 45 = 105cm
Mắt người và cá cùng cách mặt nước là 60cm, cùng nằm trên một mặt phẳng vuông góc với mặt nước. Biết chiết suất của nước là n = 4/3. Cá thấy người cách mình bao nhiêu?
Khi cá nhìn thấy người thì tia sáng từ người đến mắt cá (hình vẽ)
+ Gọi M là mắt thật và M’ là ảnh của mắt người mà cá nhìn thấy
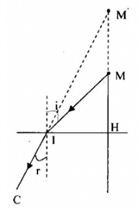
Từ hình vẽ, ta có: \(\left\{ \begin{array}{l}\tan i = \frac{{HI}}{{HM}}\\{\mathop{\rm t}\nolimits} {\rm{anr}} = \frac{{HI}}{{HM'}}\end{array} \right.\)
Để nhìn rõ, thì góc r- bé lên i bé
i, r bé \( \to \left\{ \begin{array}{l}\tan i \approx \sin i \approx i\\{\mathop{\rm t}\nolimits} {\rm{anr}} \approx {\mathop{\rm s}\nolimits} {\rm{inr}} \approx r\end{array} \right.\)
Theo định luật khúc xạ ánh sáng, ta có:
\(\sin i = n{\mathop{\rm s}\nolimits} {\rm{inr}} \to \frac{{\sin i}}{{{\mathop{\rm s}\nolimits} {\rm{inr}}}} = n \leftrightarrow \frac{{HM'}}{{HM}} = n \to HM' = HM.n = 60.\frac{4}{3} = 80cm\)
=>Vậy con cá sẽ nhìn thấy mắt người cách mắt nó đoạn : 60 + 80 = 140cm
Đáy của một cốc thủy tinh là một bản mặt song song chiết suất n = 1,5. Đặt cốc lên một trang sách rồi nhìn qua đáy cốc theo phương gần thẳng đứng thì thấy dòng chữ trên trang sách dường như nằm trong thủy tinh, cách mặt trong của đáy 0,6cm. Bề dày của đáy cốc là:
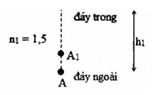
Coi đáy cốc thủy tinh là một bản mặt song song có độ dày là h1, ảnh của điểm A qua bản mặt song song thủy tinh là A1.
Độ dịch chuyển ảnh A1 so với A là:
\(A{A_1} = {h_1}\left( {1 - \frac{1}{n}} \right) = {h_1}\left( {1 - \frac{1}{{1,5}}} \right) = \frac{{h{}_1}}{3}\)
Theo đề bài, ta có: ảnh A1 cách đáy trong đoạn 0,6cm
\( \to A{A_1} = {h_1} - 0,6 \leftrightarrow \frac{{{h_1}}}{3} = {h_1} - 0,6 \to {h_1} = 0,9cm\)
Cho một khối thủy tinh dạng bán cầu có bán kính \(R\), chiết suất \(n = 1,5\). Chiếu thẳng góc tới mặt phẳng của bán cầu một tia sáng \(SI\). Biết điểm tới \(I\) cách tâm \(O\) của khối bán cầu đoạn \(0,5R\). Tia ló ra khỏi bán cầu lệch với phương \(OJ\) một góc bằng bao nhiêu?
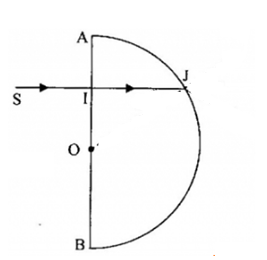
Ta có: Tia sáng đi thẳng qua mặt phẳng AB của khối bán cầu, tới mặt cầu tại \(J\) với góc tới là \(i\)
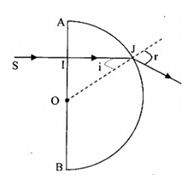
Từ hình ta có: \(\sin i = \dfrac{{OI}}{{OJ}} = \dfrac{{0,5R}}{R} = 0,5\)
Mặt khác, theo định luật khúc xạ ánh sáng, ta có: \(n\sin i = {\mathop{\rm s}\nolimits} {\rm{inr}} \leftrightarrow 1,5.0,5 = {\mathop{\rm s}\nolimits} {\rm{inr}} \to r = 48,{59^0}\)
Một bản mặt song song có bề dày 10 cm, chiết suất n = 1,5 được đặt trong không khí. Chiếu tới bản một tia sáng SI có góc tới là 450. Tính khoảng cách giữa giá của tia ló và tia tới:
Góc tới i1 = 45o.
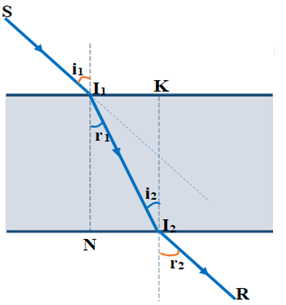
Theo định luật khúc xạ:
+ Tại I1: \(\sin {i_1}\; = n.\sin {r_1}\,\,\,\left( 1 \right)\)
+ Tại I2: \(n.\sin {i_2}\; = \sin {r_2}\,\,\,\left( 2 \right)\)
+ Vì bản mặt song song nên pháp tuyến của mặt trước và mặt sau của bản song song với nhau, từ hình vẽ \( \Rightarrow {i_2} = {r_1}\,\,\,\,\,\,\left( 3 \right)\)
Từ (1), (2) và (3) \( \Rightarrow {r_2}\; = {i_1}\; = {45^0}\;\)
Tia ló I2R song song với tia tới SI
+ Bề dày e = 10 cm; chiết suất n = 1,5
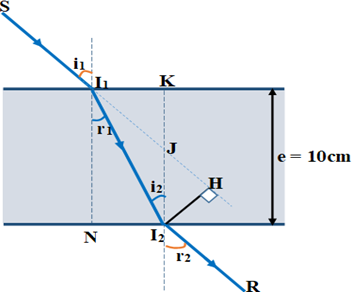
Ta có: \(\sin {i_1}\; = n.\sin {r_1}\; \Rightarrow \sin {r_1}\; = \dfrac{{\sin {i_1}}}{n} = \dfrac{{\sin {{45}^0}}}{{1,5}} = 0,4714 \Rightarrow {r_1}\; = 28,{13^0}\)
Từ hình vẽ, khoảng cách giữa giá của tia ló và tia tới bằng đường cao I2H của tam giác vuông I1I2H
\( \Rightarrow {I_2}H = {I_1}{I_2}.\sin \widehat {{I_2}{I_1}H} = {I_1}{I_2}.\sin \left( {{i_1} - {r_1}} \right)\)
Mà: \({I_1}{I_2} = \dfrac{{{I_1}N}}{{\cos {r_1}}} = \dfrac{e}{{\cos {r_1}}}\)
\( \Rightarrow {I_2}H = \dfrac{e}{{\cos {r_1}}}.\sin \left( {{i_1} - {r_1}} \right) = \dfrac{{10}}{{\cos 28,13}}.\sin \left( {45 - 28,13} \right) = 3,3cm\)
Vậy khoảng cách giữa giá của tia ló và tia tới là I2H = 3,3cm
Có ba môi trường trong suốt (1), (2), (3). Với cùng góc tới i, một tia sáng khúc xạ như hình 26.8 khi truyền từ (1) vào (2) và từ (1) vào (3).
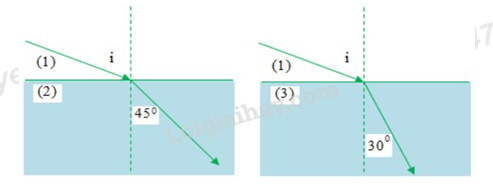
Vẫn với góc tới i, khi tia sáng truyền từ (2) vào (3) thì góc khúc xạ là bao nhiêu (tính tròn số)?
+ Khi tia sáng truyền từ môi trường (1) vào môi trường (2):
\({n_1}\sin i = {n_2}\sin 45{\rm{ }}\,\,\,\left( 1 \right)\)
+ Khi tia sáng truyền từ môi trường (1) vào môi trường (3):
\({n_1}\sin i = {n_3}\sin 30\;\,\,{\rm{ }}\left( 2 \right)\)
Từ (1) và (2) ta có: \(\dfrac{{{n_3}sin30}}{{{n_2}sin45}} = 1 \Rightarrow \dfrac{{{n_3}}}{{{n_2}}} = \dfrac{{sin45}}{{sin30}} = \sqrt 2 \)
+ Khi tia sáng truyền từ môi trường (2) vào môi trường (3) ta có:
\({n_2}\sin i = {n_3}\sin r \Rightarrow \sin r = \dfrac{{{n_2}}}{{{n_3}}}.\sin i = \dfrac{1}{{\sqrt 2 }}\sin i\)
Góc tới i chưa biết nên không xác định được góc khúc xạ r.
Tia sáng truyền từ nước và khúc xạ ra không khí. Tia khúc xạ và tia phản xạ ở mặt nước vuông góc với nhau. Nước có chiết suất là \(\dfrac{4}{3}\). Góc tới của tia sáng là bao nhiêu (tính tròn số)?
+ Tia tới SI, tia phản xạ IS’ và tia khúc xạ IR
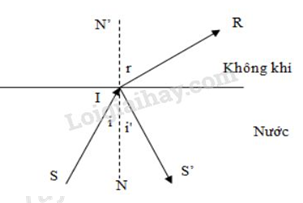
+ Góc tới, góc phản xạ và góc khúc xạ lần lượt là:
Tia khúc xạ và tia phản xạ ở mặt nước vuông góc với nhau \( \Rightarrow \widehat {S'IR} = {90^0}\)
Lại có:
\(\begin{array}{l}\widehat {NIN'} = i' + \widehat {S'IR} + r = {180^0} \Rightarrow i' + r = {180^0} - \widehat {S'IR} = {180^0} - {90^0} = {90^0}\\ \Rightarrow i' + r = {90^0}\end{array}\)
+ Theo định luật phản xạ ánh sáng: \(i = i' \Rightarrow i + r = {90^0} \Rightarrow r = {90^0} - i\)
+ Theo định luật khúc xạ ánh sáng ta có:
\(\begin{array}{l}{n_1}\sin i = {n_2}{\mathop{\rm s}\nolimits} {\rm{inr}} \Leftrightarrow \dfrac{4}{3}\sin i = 1.\sin \left( {90 - i} \right)\\ \Leftrightarrow \dfrac{4}{3}\sin i = \cos i \Rightarrow \tan i = \dfrac{3}{4} \Rightarrow i \approx {37^0}\end{array}\)
Một khối thủy tinh P có chiết suất \(n = 1,5\). Biết tiết diện thẳng là một tam giác ABC vuông cân tại B. Chiếu vuông góc tới mặt AB một chùm sáng song song SI. Góc D hợp bởi tia ló và tia tới là:
Hướng dẫn giải:
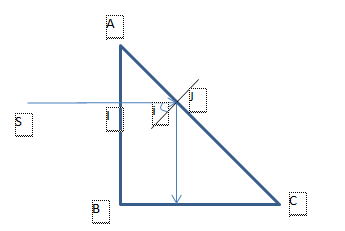
Tia SI đi đến mặt vuông góc với AB nên truyền thẳng đến mặt AC tại J với góc tới i.
∆ABC vuông cân tại B nên => \(i = {45^0}\)
Góc giới hạn phản xạ toàn phần: \(\sin {i_{gh}} = \frac{{{n_{kk}}}}{n} = \frac{1}{{1,5}} \to {i_{gh}} = 41,{8^0}\)
nhận thấy \(i > {i_{gh}}\) => tại J xảy ra hiện tượng phản xạ toàn phần với góc phản xạ 450 => Tia phản xạ vuông góc với BC
=> Góc hợp bởi tia ló và tia tới là: \(D = {90^0}\)
Chiết suất của nước là \(\frac{4}{3}\). Một người nhìn một hòn sỏi nhỏ S nằm ở đáy một bể nước sâu 1,2m theo phương gần vuông góc với mặt nước, thấy ảnh S’ nằm cách mặt nước một khoảng bằng:
Vẽ hình :
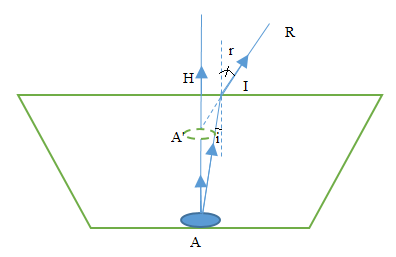
Trong tam giác AIH ta có \(\sin i = \frac{{HI}}{{AI}}\)
Áp dụng định luật khúc xạ ánh sáng ta có :
\(\frac{{\sin i}}{{\sin r}} = \frac{{{n_2}}}{{{n_1}}} \Rightarrow \sin r = {n_{nc}}.\sin i = 1,33.\frac{{HI}}{{AI}}\)
Trong tam giác HIA’ ta có:
\(\tan r = \frac{{HI}}{{HA'}} \Rightarrow HA' = \frac{{HI}}{{\tan r}}\)
Vì các góc i và r đều rất nhỏ nên ta lấy gần đúng tan r ≈ sin r ≈ r
Do đó ta có :
\(HA' = \frac{{HI}}{{\tan r}} \approx \frac{{HI}}{{\sin r}} = \frac{{HI}}{{{n_{nc}}.\frac{{HI}}{{AH}}}} = \frac{{AH}}{{{n_{nc}}}} = \frac{{1,2}}{{\frac{4}{3}}} = 0,9m = 90cm\)
Một tấm gỗ hình tròn bán kính 4cm, ở tâm O cắm thẳng góc một đinh OA. Thả miễng gỗ nổi trong một chậu đựng nước chiết suất n = 1,33. Đinh OA ở trong nước, cho OA = 6cm. Mắt đặt trong không khí sẽ thấy đầu A cách mặt nước một khoảng lớn nhất là
Ta có hình vẽ :
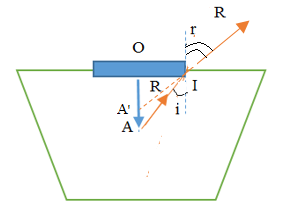
Ta có thể nhìn thấy ảnh của đinh OA lớn nhất khi nhìn theo tia khúc xạ IR như hình vẽ.
Trong tam giác OAI ta có :
\(\sin i = \frac{R}{{AI}} = \frac{R}{{\sqrt {{R^2} + {h^2}} }}\)
Áp dụng định luật khúc xạ ánh sáng ta có :
\(\begin{array}{l}
\frac{{\sin i}}{{\sin r}} = \frac{{{n_2}}}{{{n_1}}} \Rightarrow \sin r = {n_{nc}}.\sin i = 1,33.\frac{R}{{\sqrt {{R^2} + {h^2}} }}\\
\Rightarrow \sin r = 1,33.\frac{4}{{\sqrt {{4^2} + {6^2}} }} = 0,7378 \Rightarrow r = {47^0}32'
\end{array}\)
Trong tam giác OIA’ ta có :
\(\tan r = \frac{{OI}}{{OA'}} \Rightarrow OA' = \frac{{OI}}{{\tan r}} = \frac{R}{{\tan r}} = \frac{4}{{\tan r}} = 3,66cm\)
Chiếu một chùm sáng đơn sắc song song có dạng một dải mỏng và có bề rộng 10 mm từ không khí vào bề mặt của một chất lỏng có chiết suất n = 1,5 với góc tới 450. Dải sáng nằm trong một mặt phẳng vuông góc với mặt thoáng của chất lỏng. Bề rộng của dải tia sáng khi nó truyền trong chất lỏng là:
Ta có hình vẽ:
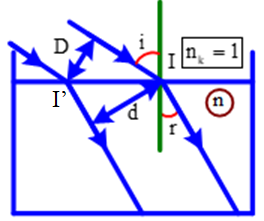
Áp dụng công thức định luật khúc xạ ánh sáng, ta có:
\(\sin i = n\sin r \Rightarrow \sin r = \dfrac{{\sin i}}{n} = \dfrac{{\sin {{45}^0}}}{{1,5}} \Rightarrow r \approx 28,{13^0}\)
Từ hình vẽ ta thấy: \(II' = \dfrac{D}{{\cos i}} = \dfrac{d}{{\cos r}} \Rightarrow d = D\dfrac{{\cos r}}{{\cos i}}\)
\( \Rightarrow d = 10.\dfrac{{\cos {{28}^0}}}{{\cos {{45}^0}}} \approx 12,47\,\,\left( {mm} \right)\)
Một cái máng nước sâu 30 cm rộng 40 cm có hai thành bên thẳng đứng. Lúc máng cạn nước thì bóng râm của thành A kéo dài tới đúng chân thành B đối diện. Người ta đổ nước vào máng đến độ cao h bằng 2/3 độ cao của thành thì bóng của thành A ngắn bớt đi một đoạn d so với trước. Biết chiết suất của nước là \(n = \frac{4}{3}\). Xác định d.
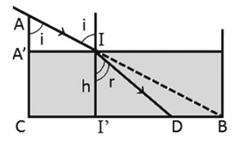
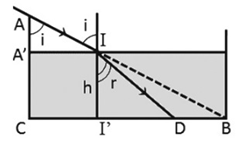
Từ hình vẽ ta thấy: \(\sin i = \frac{{A'I}}{{AI}} = \frac{{CB}}{{AB}} = \frac{{40}}{{\sqrt {{{30}^2} + {{40}^2}} }} = 0,8\)
\( \Rightarrow \frac{1}{{{{\sin }^2}i}} = 1 + \frac{1}{{{{\tan }^2}i}} \Rightarrow \frac{1}{{0,{8^2}}} = 1 + \frac{1}{{{{\tan }^2}i}} \Rightarrow \tan i = \frac{4}{3}\)
Áp dụng công thức định luật khúc xạ ánh sáng, ta có:
\(\sin i = n\sin r \Rightarrow \sin r = \frac{{\sin i}}{n} = \frac{{0,8}}{{\frac{4}{3}}} = 0,6\)
\( \Rightarrow \frac{1}{{{{\sin }^2}r}} = 1 + \frac{1}{{{{\tan }^2}r}} \Rightarrow \frac{1}{{0,{6^2}}} = 1 + \frac{1}{{{{\tan }^2}r}} \Rightarrow \tan r = 0,75\)
Lại có: \(h = II' = \frac{2}{3}AC = \frac{2}{3}.30 = 20{\mkern 1mu} {\mkern 1mu} \left( {cm} \right)\)
Ta có:
\(\begin{array}{*{20}{l}}{\left\{ {\begin{array}{*{20}{l}}{I'B = h.\tan i}\\{I'D = h.\tan r}\end{array}} \right. \Rightarrow d = I'B - I'D = h\left( {\tan i - \tan r} \right)}\\{ \Rightarrow d = 20.\left( {\frac{4}{3} - 0,75} \right) \approx 11,7{\mkern 1mu} {\mkern 1mu} \left( {cm} \right)}\end{array}\)
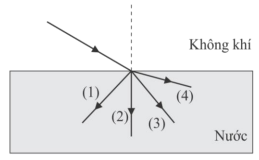
Trong một tiết kiểm tra, có bốn học sinh vẽ đường truyền của một tia sáng đơn sắc từ không khí vào nước tương ứng với các đường kẻ (1), (2), (3), (4) như hình dưới. Đường kẻ nào vẽ đúng đường truyền của tia sáng đơn sắc trong trường hợp đang xét?
Ta có: \({n_1} < {n_2}\)
\({n_1}\sin i = {n_2}\sin r\) \(\dfrac{{\sin i}}{{\sin r}} = \dfrac{{{n_2}}}{{{n_1}}} > 1\)
\( \Rightarrow i > r\)
Mặt khác: Theo định luật khúc xạ ánh sáng thì:
+ Tia khúc xạ nằm trong mặt phẳng tới
+ Tia tới và tia khúc xạ nằm ở hai bên pháp tuyến tại điểm tới.
Vậy đường kẻ vẽ đúng đường truyền của tia sáng đơn sắc trong trường hợp đang xét là đường (3).
Trong sợi quang hình trụ gồm phần lõi có chiết suất \(n=1,60\) và phần vỏ bọc có chiết suất \({n_0} = 1,41\). Trong không khí, một tia sáng tới mặt trước của sợi quang tại điểm O (O nằm trên trục của sợi quang) với góc tới \(\alpha \) rồi khúc xạ vào phần lõi (như hình bên). Để tia sáng chỉ truyền đi trong phần lõi thì giá trị lớn nhất của góc \(\alpha \) gần nhất với giá trị nào sau đây?
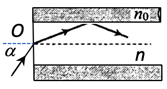
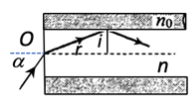
Ta có: \(\sin \alpha = n.\sin \,r \Rightarrow \sin \,r = \dfrac{{\sin \alpha }}{n}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \,\,\left( 1 \right)\)
Lại có: \(r + i = {90^0} \Rightarrow \sin i = \cos \,r\)
Để xảy ra phản xạ toàn phần tại mặt phân cách phần lõi và vỏ thì:
\(\begin{array}{l}
i \ge {i_{gh}} \Rightarrow \sin i \ge \dfrac{{{n_0}}}{n}\\
\Rightarrow \cos r \ge \dfrac{{{n_0}}}{n}{\mkern 1mu} \Leftrightarrow \sqrt {1 - {{\sin }^2}r} \ge \dfrac{{{n_0}}}{n}\,\,\,\,\left( 2 \right)
\end{array}\)
Từ (1) và (2) suy ra:
\(\begin{array}{l}
\sqrt {1 - {{\left( {\dfrac{{\sin \alpha }}{n}} \right)}^2}} \ge \dfrac{{{n_0}}}{n} \Leftrightarrow {n^2} - {\sin ^2}\alpha \ge n_0^2\\
\Leftrightarrow {\sin ^2}\alpha \le {n^2} - n_0^2\\
\Leftrightarrow \sin \alpha \le \sqrt {1,{6^2} - 1,{{41}^2}} \Rightarrow \alpha \le 49,{134^0}\\
\Rightarrow {\alpha _{\max }} = 49,{134^0}
\end{array}\)
Một người nhìn thấy con cá ở trong nước. Hỏi muốn đâm trúng con cá thì người đó phải phóng mũi lao vào chỗ nào?
Gọi O là vị trí của con cá trong nước.
Do hiện tượng khúc xạ và do chiết suất của nước lớn hơn chiết suất của không khí nên ảnh của con cá sẽ ở vị trí O’ như hình vẽ.
Như vậy, người đó nhìn thấy con cá dường như gần mặt nước hơn. Để đâm trúng con cá thì người đó phải phóng mũi lao vào phía dưới vị trí mà người đó nhìn thấy con cá.