Câu hỏi:
2 năm trước
Một cái máng nước sâu 30 cm rộng 40 cm có hai thành bên thẳng đứng. Lúc máng cạn nước thì bóng râm của thành A kéo dài tới đúng chân thành B đối diện. Người ta đổ nước vào máng đến độ cao h bằng 2/3 độ cao của thành thì bóng của thành A ngắn bớt đi một đoạn d so với trước. Biết chiết suất của nước là \(n = \frac{4}{3}\). Xác định d.
Trả lời bởi giáo viên
Đáp án đúng: c
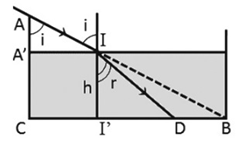
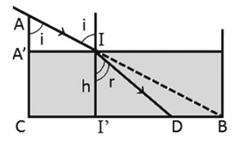
Từ hình vẽ ta thấy: \(\sin i = \frac{{A'I}}{{AI}} = \frac{{CB}}{{AB}} = \frac{{40}}{{\sqrt {{{30}^2} + {{40}^2}} }} = 0,8\)
\( \Rightarrow \frac{1}{{{{\sin }^2}i}} = 1 + \frac{1}{{{{\tan }^2}i}} \Rightarrow \frac{1}{{0,{8^2}}} = 1 + \frac{1}{{{{\tan }^2}i}} \Rightarrow \tan i = \frac{4}{3}\)
Áp dụng công thức định luật khúc xạ ánh sáng, ta có:
\(\sin i = n\sin r \Rightarrow \sin r = \frac{{\sin i}}{n} = \frac{{0,8}}{{\frac{4}{3}}} = 0,6\)
\( \Rightarrow \frac{1}{{{{\sin }^2}r}} = 1 + \frac{1}{{{{\tan }^2}r}} \Rightarrow \frac{1}{{0,{6^2}}} = 1 + \frac{1}{{{{\tan }^2}r}} \Rightarrow \tan r = 0,75\)
Lại có: \(h = II' = \frac{2}{3}AC = \frac{2}{3}.30 = 20{\mkern 1mu} {\mkern 1mu} \left( {cm} \right)\)
Ta có:
\(\begin{array}{*{20}{l}}{\left\{ {\begin{array}{*{20}{l}}{I'B = h.\tan i}\\{I'D = h.\tan r}\end{array}} \right. \Rightarrow d = I'B - I'D = h\left( {\tan i - \tan r} \right)}\\{ \Rightarrow d = 20.\left( {\frac{4}{3} - 0,75} \right) \approx 11,7{\mkern 1mu} {\mkern 1mu} \left( {cm} \right)}\end{array}\)
Hướng dẫn giải:
Công thức định luật khúc xạ ánh sáng: \(\sin i = n\sin r\)
Công thức lượng giác: \(\dfrac{1}{{{{\sin }^2}x}} = 1 + \dfrac{1}{{{{\tan }^2}x}}\)
