Câu hỏi:
2 năm trước
Mắt người và cá cùng cách mặt nước là 60cm, cùng nằm trên một mặt phẳng vuông góc với mặt nước. Biết chiết suất của nước là n = 4/3. Hỏi người thấy cá cách mình bao xa?
Trả lời bởi giáo viên
Đáp án đúng: d
Khi người nhìn thấy cá thì tia sáng từ cá đến mắt người (hình vẽ)
+ Vì mắt nhìn xuống đáy chậu gần vuông góc nên góc r rất nhỏ
=> i cũng rất nhỏ
+ Gọi A là cá thật và A’ là ảnh của cá
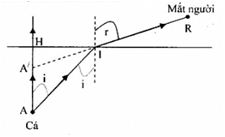
Từ hình vẽ, ta có: \(\left\{ \begin{array}{l}\tan i = \frac{{HI}}{{HA}} \approx \sin i \approx i\\{\mathop{\rm t}\nolimits} {\rm{anr}} = \frac{{HI}}{{HA'}} \approx {\mathop{\rm s}\nolimits} {\rm{inr}} \approx {\rm{r}}\end{array} \right.\)
Theo định luật khúc xạ ánh sáng, ta có:
\(n\sin i = {\mathop{\rm s}\nolimits} {\rm{inr}} \to \frac{{\sin i}}{{{\mathop{\rm s}\nolimits} {\rm{inr}}}} = \frac{1}{n} \leftrightarrow \frac{{HA'}}{{HA}} = \frac{1}{n} \to HA' = \frac{{HA}}{n} = \frac{{60}}{{\frac{4}{3}}} = 45cm\)
=> Người nhìn thấy cá cách mắt mình đoạn 60 + 45 = 105cm
Hướng dẫn giải:
+ Vẽ đường truyền tia sáng qua lưỡng chất phẳng
+ Sử dụng hệ thức lượng trong tam giác
+ Vận dụng biểu thức định luật khúc xạ ánh sáng: \({n_1}\sin i = {n_2}{\mathop{\rm s}\nolimits} {\rm{inr}}\)
