Câu hỏi:
2 năm trước
Bể chứa nước có thành cao 80cm và đáy phẳng dài 120cm. Độ cao mực nước trong bể là 60cm, chiết suất của nước là 4/3. Ánh nắng chiếu theo phương nghiêng một góc 300 so với phương ngang. Độ dài của bóng đen tạo thành dưới đáy bể là:
Trả lời bởi giáo viên
Đáp án đúng: c
Ta có, ánh nắng chiếu nghiêng một góc 300 so với phương ngang => i = 600
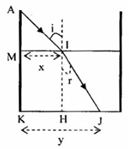
Từ hình vẽ ta có:
\(\tan i = \frac{x}{{MA}} \to x = MAtan60 = 20\sqrt 3 cm\)
\({\mathop{\rm s}\nolimits} {\rm{inr}} = \frac{{HJ}}{{\sqrt {H{I^2} + H{J^2}} }}\)
+ Theo định luật khúc xạ ánh sáng, ta có:
\(\begin{array}{l}\frac{{\sin i}}{{{\mathop{\rm s}\nolimits} {\rm{inr}}}} = n \leftrightarrow \frac{{\sin {{60}^0}}}{{\frac{{HJ}}{{\sqrt {H{I^2} + H{J^2}} }}}} = \frac{4}{3} \to \frac{{HJ}}{{\sqrt {H{I^2} + H{J^2}} }} = \frac{{3\sqrt 3 }}{8}\\ \leftrightarrow \frac{{H{J^2}}}{{H{I^2} + H{J^2}}} = \frac{{27}}{{64}} \to H{J^2} = \frac{{27}}{{37}}H{I^2} \to HJ = \sqrt {\frac{{27}}{{37}}} .60 = 51,25cm\end{array}\)
Vậy vệt sáng ở dưới đáy bể là: \(y = x + HJ = 20\sqrt 3 + 51,25 = 85,9cm\)
Hướng dẫn giải:
+ Vẽ đường truyền tia sáng qua lưỡng chất phẳng
+ Sử dụng hệ thức lượng trong tam giác
+ Vận dụng biểu thức định luật khúc xạ ánh sáng: \({n_1}\sin i = {n_2}{\mathop{\rm s}\nolimits} {\rm{inr}}\)
