Câu hỏi:
2 năm trước
Một bản mặt song song có bề dày 10 cm, chiết suất n = 1,5 được đặt trong không khí. Chiếu tới bản một tia sáng SI có góc tới là 450. Tính khoảng cách giữa giá của tia ló và tia tới:
Trả lời bởi giáo viên
Đáp án đúng: d
Góc tới i1 = 45o.
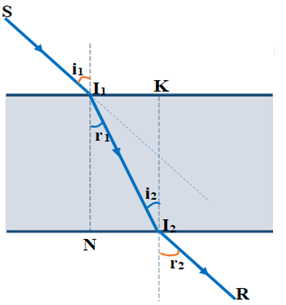
Theo định luật khúc xạ:
+ Tại I1: \(\sin {i_1}\; = n.\sin {r_1}\,\,\,\left( 1 \right)\)
+ Tại I2: \(n.\sin {i_2}\; = \sin {r_2}\,\,\,\left( 2 \right)\)
+ Vì bản mặt song song nên pháp tuyến của mặt trước và mặt sau của bản song song với nhau, từ hình vẽ \( \Rightarrow {i_2} = {r_1}\,\,\,\,\,\,\left( 3 \right)\)
Từ (1), (2) và (3) \( \Rightarrow {r_2}\; = {i_1}\; = {45^0}\;\)
Tia ló I2R song song với tia tới SI
+ Bề dày e = 10 cm; chiết suất n = 1,5
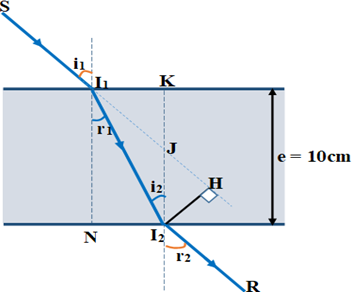
Ta có: \(\sin {i_1}\; = n.\sin {r_1}\; \Rightarrow \sin {r_1}\; = \dfrac{{\sin {i_1}}}{n} = \dfrac{{\sin {{45}^0}}}{{1,5}} = 0,4714 \Rightarrow {r_1}\; = 28,{13^0}\)
Từ hình vẽ, khoảng cách giữa giá của tia ló và tia tới bằng đường cao I2H của tam giác vuông I1I2H
\( \Rightarrow {I_2}H = {I_1}{I_2}.\sin \widehat {{I_2}{I_1}H} = {I_1}{I_2}.\sin \left( {{i_1} - {r_1}} \right)\)
Mà: \({I_1}{I_2} = \dfrac{{{I_1}N}}{{\cos {r_1}}} = \dfrac{e}{{\cos {r_1}}}\)
\( \Rightarrow {I_2}H = \dfrac{e}{{\cos {r_1}}}.\sin \left( {{i_1} - {r_1}} \right) = \dfrac{{10}}{{\cos 28,13}}.\sin \left( {45 - 28,13} \right) = 3,3cm\)
Vậy khoảng cách giữa giá của tia ló và tia tới là I2H = 3,3cm
Hướng dẫn giải:
Định luật khúc xạ ánh sáng: \({n_1}\sin i = {n_2}\sin r\)
