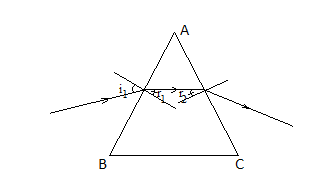
Chiếu một tia sáng đến lăng kính thì thấy tia ló ra là một tia sáng đơn sắc. Có thể kết luận tia sáng chiếu tới lăng kính là ánh sáng:
Tia sáng gồm nhiều ánh sáng đơn sắc, khi đi qua lăng kính bị tán sắc thành nhiều ánh sáng đơn sắc
→ Tia ló ra là một tia sáng đơn sắc → tia sáng chiếu tới là ánh sáng đơn sắc.
Chiếu vào mặt bên một lăng kính có góc chiết quang \(A = {60^0}\) một chùm ánh sáng trắng hẹp coi như một tia sáng . Biết góc lệch của tia màu vàng là cực tiểu. Chiết suất của lăng kính với tia màu vàng là \({n_v} = 1,52\) và màu tím \({n_t} = 1,54\). Góc ló của tia màu tím bằng:
Tia màu vàng có góc lệch cực tiểu, ta có:
\(\begin{array}{l}\sin \frac{{{D_{\min }} + A}}{2} = {n_v}\sin \frac{A}{2} \Rightarrow \sin \frac{{{D_{\min }} + {{60}^0}}}{2} = 1,52.\sin \frac{{{{60}^0}}}{2}\\ \Rightarrow \sin \frac{{{D_{\min }} + {{60}^0}}}{2} = 0,76 \Rightarrow \frac{{{D_{\min }} + {{60}^0}}}{2} = 49,{46^0} \Rightarrow {D_{\min }} = 38,{92^0}\end{array}\)
Lại có: \({D_{\min }} = 2{i_{\min }} - A \Rightarrow {i_{\min }} = \frac{{{D_{\min }} + A}}{2} = 49,{46^0}\)
Tia sáng rất hẹp → góc tới của tia màu tím bằng góc tới của tia màu vàng: \({i_{1t}} = {i_{\min }} = 49,{46^0}\)
Áp dụng công thức lăng kính, ta có:
\(\begin{array}{l}\sin {i_{1t}} = {n_t}\sin {r_{1t}} \Rightarrow \sin {r_{1t}} = \frac{{\sin {i_{1t}}}}{{{n_t}}} = \frac{{\sin 49,46}}{{1,54}}\\ \Rightarrow \sin {r_{1t}} = \frac{{0,76}}{{1,54}} = 0,4935 \Rightarrow {r_{1t}} = 29,{57^0}\end{array}\)
Lại có: \({r_{1t}} + {r_{2r}} = A \Rightarrow {r_{2t}} = A - {r_{1t}} = {60^0} - 29,{57^0} = 30,{43^0}\)
\(\sin {i_{2t}} = {n_t}\sin {r_{2t}} = 1,54.\sin 30,{43^0} \Rightarrow \sin {i_{2t}} \approx 0,78 \Rightarrow {i_{2t}} = 51,{26^0} \approx 51,{3^0}\)
Tiết diện thẳng của một lăng kính là tam giác đều. Một tia sáng đơn sắc chiếu tới mặt bên lăng kính và cho tia ló đi ra từ một mặt bên khác. Nếu góc tới và góc ló là \({45^0}\) thì góc lệch giữa tia tới và tia ló là
Ta thấy \({i_1} = {i_2} = {45^0} \to \) tia sáng có góc lệch cực tiểu
Góc lệch cực tiểu giữa tia tới và tia ló là:
\({D_m} = 2{i_m} - A = {2.45^0} - {60^0} = {30^0}\)
Phát biểu nào sau đây là không đúng? Chiếu một chùm sáng vào mặt bên của một lăng kính đặt trong không khí:
A, B, D – đúng
C – sai vì: có trường hợp tia sáng bị phản xạ toàn phần trong lăng kính
Chiếu một chùm sáng song song tới lăng kính. Tăng dần góc tới i từ giá trị nhỏ nhất thì:
Ta có, góc lệch \(D = {i_1} + {i_2} - A\)
Góc lệch đạt giá trị cực tiểu \({D_m} = 2{i_m} - A\) khi \({i_1} = {i_2} = {i_m}\)
=> Khi tăng giá trị góc tới \(i\) từ giá trị nhỏ nhất là \({0^0}\) thì góc lệch giảm dần xuống giá trị cực tiểu rồi lại tăng
Chiếu một chùm sáng đến lăng kính thì thấy tia ló ra là chùm ánh sáng nhiều màu sắc khác nhau từ đỏ đến tím. Có thể kết luận chùm sáng chiếu tới lăng kính là ánh sáng:
Chùm ánh sáng trắng khi đi qua lăng kính sẽ bị phân tích thành nhiều chùm sáng đơn sắc khác nhau do chiết suất của chất làm lăng kính đối với mỗi ánh sáng khác nhau là khác nhau.
=> Chiếu một chùm sáng đến lăng kính thì thấy tia ló ra là chùm ánh sáng nhiều màu sắc khác nhau từ đỏ đến tím => ánh sáng đó là ánh sáng trắng
Sử dụng hình vẽ về đường đi của tia sáng qua lăng kính: SI là tia tới, JR là tia ló, D là góc lệch giữa tia tới và tia ló, n là chiết suất của chất làm lăng kính. Công thức nào trong các công thức sau là đúng?
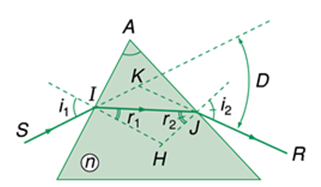
\(\begin{array}{l}\sin {i_1} = n\sin {r_1};{\rm{ }}\sin {i_2} = n\sin {r_2}\\{r_1} + {r_2} = A\\D = {i_1} + {i_2} - A\end{array}\)
+ Khi góc lệch cực tiểu: \(\sin \dfrac{{{D_m} + A}}{2} = n\sin \dfrac{A}{2}\)
Ta suy ra các phương án: A, B, C – sai
Phương án D - đúng
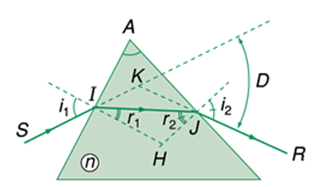
Sử dụng hình vẽ về đường đi của tia sáng qua lăng kính: SI là tia tới, JR là tia ló, D là góc lệch giữa tia tới và tia ló, n là chiết suất của chất làm lăng kính.Công thức nào trong các công thức sau đây là sai?

\(\begin{array}{l}\sin {i_1} = n\sin {r_1};{\rm{ }}\sin {i_2} = n\sin {r_2}\\{r_1} + {r_2} = A\\D = {i_1} + {i_2} - A\end{array}\)
+ Khi góc lệch cực tiểu: \(\sin \dfrac{{{D_m} + A}}{2} = n\sin \dfrac{A}{2}\)
=> A, B, C đều đúng
D – sai vì: \(A = {r_1} + {r_2}\)
Một lăng kính thủy tinh có chiết suất \(n = \sqrt 2 \). Tiết diện thẳng của lăng kính là một tam giác đều ABC. Chiếu một tia sáng nằm trong mặt phẳng của tiết diện thẳng, tới AB với góc tới \({i_1} = {45^0}\). Góc lệch D của lăng kính có giá trị là:
+ Áp dụng định luật khúc xạ ánh sáng tại I, ta có:
\(\begin{array}{l}\sin {i_1} = n\sin {r_1}\\ \Leftrightarrow \sin {45^0} = \sqrt 2 {\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_1}\\ \Rightarrow {\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_1} = \dfrac{1}{2} \Rightarrow {r_1} = {30^0}\end{array}\)
+ Lại có góc chiết quang
\(\begin{array}{l}A = {60^0} = {r_1} + {r_2}\\ \Rightarrow {r_2} = A - {r_1} = {60^0} - {30^0} = {30^0}\end{array}\)
+ Áp dụng định luật khúc xạ ánh sáng tại J, ta có:
\(\begin{array}{l}\sin {i_2} = n\sin {r_2}\\ \Leftrightarrow \sin {i_2} = \sqrt 2 \sin {30^0} = \dfrac{{\sqrt 2 }}{2}\\ \Rightarrow {i_2} = {45^0}\end{array}\)
+ Góc lệch của lăng kính: \(D = {i_1} + {i_2} - A = {45^0} + {45^0} - {60^0} = {30^0}\)
Một lăng kính đặt trong không khí, có góc chiết quang \(A = {30^0}\) nhận một tia sáng tới vuông góc với mặt bên \(AB\) và tia ló sát mặt bên \(AC\) của lăng kính. Chiết suất \(n\) của lăng kính
Tia tới vuông góc với mặt bên \(AB\) và tia ló sát mặt bên \(AC\)\( \Rightarrow \left\{ \begin{array}{l}{i_1} = {0^0}\\{i_2} = {90^0}\end{array} \right.\)
Áp dụng công thức lăng kính, ta có:
\(\begin{array}{l}\sin {i_1} = n\sin {r_1} \Rightarrow \sin {r_1} = \dfrac{{\sin {i_1}}}{n} = \dfrac{{\sin {0^0}}}{n} = 0 \Rightarrow {r_1} = {0^0}\\ \Rightarrow {r_2} = A - {r_1} = {30^0} - {0^0} = {30^0}\end{array}\)
\(\sin {i_2} = n\sin {r_2} \Rightarrow n = \dfrac{{\sin {i_2}}}{{\sin {r_2}}} = \dfrac{{\sin {{90}^0}}}{{\sin {{30}^0}}} = 2\)
Hình vẽ bên là đường truyền của tia sáng đơn sắc qua lăng kính đặt trong không khí có chiết suất \(n = \sqrt 2 \). Biết tia tới vuông góc với mặt bên AB và tia ló ra khỏi lăng kính đi là là mặt AC. Tính góc chiết quang A của lăng kính?
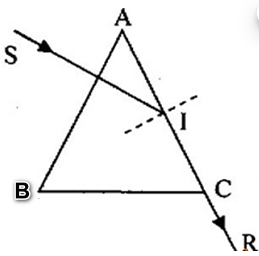
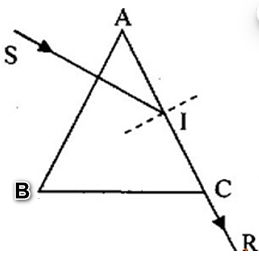
+ Vì chiếu tia tới vuông góc với mặt AB nên \({i_1} = 0 \Rightarrow {r_1} = 0\)
+ Ta có, góc chiết quang \(A = {r_1} + {r_2} = 0 + {r_2} \Rightarrow A = {r_2}\)
+ Vì tia ló đi là là mặt AC nên \({i_2} = {90^0}\)
Áp dụng định luật khúc xạ ánh sáng tại mặt AC, ta có:
\(\begin{array}{l}\sin {i_2} = n\sin {r_2}\\ \Leftrightarrow \sin {90^0} = \sqrt 2 {\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_2}\\ \Rightarrow {\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_2} = \dfrac{1}{{\sqrt 2 }} \Rightarrow {r_2} = {45^0}\end{array}\)
=> Góc chiết quang của lăng kính \(A = {r_2} = {45^0}\)
Một lăng kính thủy tinh có chiết suất \(n = 1,6\). Chiếu một tia sáng đơn sắc theo phương vuông góc với mặt bên của lăng kính. Tia sáng phản xạ toàn phần ở mặt bên của lăng kính. Tính giá trị nhỏ nhất của góc chiết quang A.
+ Ta có, chiếu tia sáng đơn sắc theo phương vuông góc với mặt bên của lăng kính
\( \Rightarrow {i_1} = 0 \Rightarrow {r_1} = {0^0}\)
+ Góc chiết quang \(A = {r_1} + {r_2} = {0^0} + {r_2} \Rightarrow A = {r_2}\)
Vì xảy ra phản xạ toàn phần nên ta suy ra \({r_2} \ge {i_{gh}} \Rightarrow A \ge {i_{gh}}\)
+ Ta có có giới hạn phản xạ toàn phần khi ánh sáng truyền từ lăng kính ra môi trường không khí bên ngoài
\(\begin{array}{l}\sin {i_{gh}} = \dfrac{{{n_{kk}}}}{{{n_{lk}}}} = \dfrac{1}{n} = \dfrac{1}{{1,6}}\\ \Rightarrow {i_{gh}} = 38,{7^0}\end{array}\)
Ta suy ra:
\(\begin{array}{l}A \ge {i_{gh}} = 38,{7^0}\\ \Rightarrow {A_{\min }} = 38,{7^0}\end{array}\)
Chọn phương án đúng. Một tia sáng tới vuông góc với mặt AB của một lăng kính có chiết suất \(n = \sqrt 2 \) và góc ở đỉnh A = 300, B là góc vuông. Góc lệch của tia sáng qua lăng kính là:
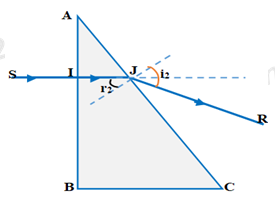
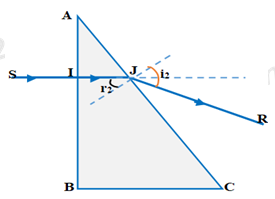
Tia tới: \(SI \bot AB \Rightarrow {i_1} = 0 \Rightarrow {r_1} = 0\)
Góc tới mặt AC: \({r_2} = \widehat A = {30^0}\)
Áp dụng định luật khúc xạ ánh sáng ta có:
\(n.\sin \,{r_2} = \sin {i_2} \Rightarrow \sin {i_2} = \sqrt 2 .\sin 30 = \dfrac{{\sqrt 2 }}{2} \Rightarrow {i_2} = {45^0}\)
Góc lệch của tia sáng qua lăng kính là:
\(D = {i_1} + {\rm{ }}{i_2} - {\rm{ }}A = 0 + {45^0} - {30^0} = {15^0}\)
Cho tia sáng truyền tới lăng kính như hình vẽ. Tia ló truyền đi đi sát mặt BC. Góc lệch tạo bởi lăng kính có giá trị nào sau đây?
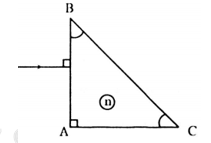
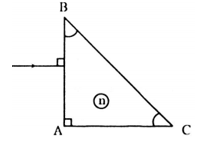
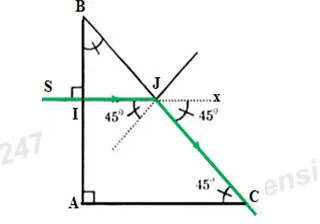

Ta có ΔABC vuông cân \( \Rightarrow \widehat B = \widehat C = {45^0}\)
\(SI \bot AB \Rightarrow \) Tia SI truyền thẳng vào môi trường trong suốt ABC mà không bị khúc xạ
→ Góc tới ở mặt AB là i1 = 0 và góc khúc xạ r1 = 0
Tia ló truyền sát mặt BC → Góc ló i2 = 900
→ Góc lệch tạo bởi lăng kính có giá trị: \(D = {i_1} + {i_2} - \widehat B = 0 + {90^0} - {\rm{ }}{45^0} = {45^0}\)
Lăng kính có chiết suất n = \(\sqrt{2}\) và góc chiết quang A= 600. Một chùm tia sáng đơn sắc hẹp được chiếu vào mặt bên AB của lăng kính với góc tới 450. Tính góc ló của tia sáng khi ra khỏi lăng kính và góc lệch của tia ló và tia tới.
Theo bài ra: i1 = 450, n =\(\sqrt{2}\)
sini1 = nsinr1 => sin450 = \(\sqrt{2}\)sinr1 => r1 = 300 => r2 = A – r1 = 300
nsinr2 = sini2 => \(\sqrt{2}\)sin300 = sini2 => i2 = 450
Góc lệch: D = (i1 + i2) – A = 300
Khi chiếu tia sáng đơn sắc qua lăng kính có tiết diện là tam giác đều với góc tới i1 = 450 thì góc khúc xạ r1 bằng góc tới r2 ( hình vẽ). Góc lệch của tia sáng qua lăng kính khi đó là
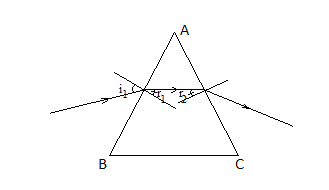
Ta có r1 + r2 = 2r1 = A = 600 => r1 = 300
Sini1 = nsinr1 => n = \(\sqrt{2}\)
nsinr2 = sini2 => \(\sqrt{2}\)sin300 = sini2 => i2 = 450
Góc lệch : D = i1 + i2 – A = 45 + 45 – 60 = 30
Lăng kính có góc chiết quang A = 300 và chiết suất n = \(\sqrt{2}\). Tia ló truyền thẳng ra không khí vuông góc với mặt thứ hai của lăng kính khi góc tới i1 có giá trị:
Tia ló truyền thẳng ra không khí vuông góc với mặt thứ hai của lăng kính => i2 = 0
Ta có: sini2 = nsinr2 => r2 = 0 => r1 = A =300
Mà sini1 = nsinr1 => sini1 = \(\sqrt{2}\) sin300 => i1 = 450
Một lăng kính có tiết diện thẳng là tam giác đều, ba mặt như nhau, chiết suất n =\(\sqrt{3}\) , được đặt trong không khí. Chiếu tia sáng đơn sắc nằm trong mặt phẳng tiết diện thẳng, vào mặt bên của lăng kính với góc tới i= 600. Góc lệch D của tia ló và tia tới bằng
Ta có sini1 = nsinr1 => r1 = 300 => r2 = 300 => i2 = 600
Góc lệch D = i1 + i2 – A = 600
Cho một lăng kính thủy tinh có tiết diện là tam giác vuông cân đặt trong không khí, góc chiết quang đối diện với mặt huyền. Nếu góc khúc xạ r1 = 300 thì góc tới r2 = ?
Áp dụng công thức lăng kính: A = r1 + r2 => 900 = 300 + r2 => r2 = 600
Qua lăng kính có chiết suất lớn hơn chiết suất môi trường, ánh sáng đơn sắc bị lệch về phía
Qua lăng kính có chiết suất lớn hơn chiết suất môi trường, ánh sáng đơn sắc bị lệch về phía đáy của lăng kính