Câu hỏi:
2 năm trước
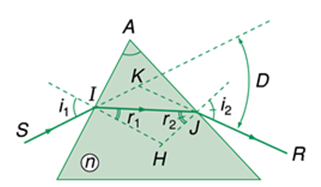
Một lăng kính thủy tinh có chiết suất \(n = 1,6\). Chiếu một tia sáng đơn sắc theo phương vuông góc với mặt bên của lăng kính. Tia sáng phản xạ toàn phần ở mặt bên của lăng kính. Tính giá trị nhỏ nhất của góc chiết quang A.
Trả lời bởi giáo viên
Đáp án đúng: c
+ Ta có, chiếu tia sáng đơn sắc theo phương vuông góc với mặt bên của lăng kính
\( \Rightarrow {i_1} = 0 \Rightarrow {r_1} = {0^0}\)
+ Góc chiết quang \(A = {r_1} + {r_2} = {0^0} + {r_2} \Rightarrow A = {r_2}\)
Vì xảy ra phản xạ toàn phần nên ta suy ra \({r_2} \ge {i_{gh}} \Rightarrow A \ge {i_{gh}}\)
+ Ta có có giới hạn phản xạ toàn phần khi ánh sáng truyền từ lăng kính ra môi trường không khí bên ngoài
\(\begin{array}{l}\sin {i_{gh}} = \dfrac{{{n_{kk}}}}{{{n_{lk}}}} = \dfrac{1}{n} = \dfrac{1}{{1,6}}\\ \Rightarrow {i_{gh}} = 38,{7^0}\end{array}\)
Ta suy ra:
\(\begin{array}{l}A \ge {i_{gh}} = 38,{7^0}\\ \Rightarrow {A_{\min }} = 38,{7^0}\end{array}\)
Hướng dẫn giải:
+ Sử dụng định luật khúc xạ ánh sáng: \({n_1}{\mathop{\rm sini}\nolimits} = {n_2}{\mathop{\rm s}\nolimits} {\rm{inr}}\)
+ Sử dụng công thức tính góc chiết quang: \(A = {r_1} + {r_2}\)
+ Sử dụng biểu thức tính góc giới hạn phản xạ toàn phần: \(\sin {i_{gh}} = \dfrac{{{n_2}}}{{{n_1}}}\)
