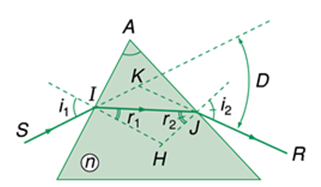
Chiếu vào mặt bên một lăng kính có góc chiết quang \(A = {60^0}\) một chùm ánh sáng trắng hẹp coi như một tia sáng . Biết góc lệch của tia màu vàng là cực tiểu. Chiết suất của lăng kính với tia màu vàng là \({n_v} = 1,52\) và màu tím \({n_t} = 1,54\). Góc ló của tia màu tím bằng:

Tia màu vàng có góc lệch cực tiểu, ta có:

\(\begin{array}{l}\sin \frac{{{D_{\min }} + A}}{2} = {n_v}\sin \frac{A}{2} \Rightarrow \sin \frac{{{D_{\min }} + {{60}^0}}}{2} = 1,52.\sin \frac{{{{60}^0}}}{2}\\ \Rightarrow \sin \frac{{{D_{\min }} + {{60}^0}}}{2} = 0,76 \Rightarrow \frac{{{D_{\min }} + {{60}^0}}}{2} = 49,{46^0} \Rightarrow {D_{\min }} = 38,{92^0}\end{array}\)

Lại có: \({D_{\min }} = 2{i_{\min }} - A \Rightarrow {i_{\min }} = \frac{{{D_{\min }} + A}}{2} = 49,{46^0}\)

Tia sáng rất hẹp → góc tới của tia màu tím bằng góc tới của tia màu vàng: \({i_{1t}} = {i_{\min }} = 49,{46^0}\)

Áp dụng công thức lăng kính, ta có:

\(\begin{array}{l}\sin {i_{1t}} = {n_t}\sin {r_{1t}} \Rightarrow \sin {r_{1t}} = \frac{{\sin {i_{1t}}}}{{{n_t}}} = \frac{{\sin 49,46}}{{1,54}}\\ \Rightarrow \sin {r_{1t}} = \frac{{0,76}}{{1,54}} = 0,4935 \Rightarrow {r_{1t}} = 29,{57^0}\end{array}\)

Lại có: \({r_{1t}} + {r_{2r}} = A \Rightarrow {r_{2t}} = A - {r_{1t}} = {60^0} - 29,{57^0} = 30,{43^0}\)

\(\sin {i_{2t}} = {n_t}\sin {r_{2t}} = 1,54.\sin 30,{43^0} \Rightarrow \sin {i_{2t}} \approx 0,78 \Rightarrow {i_{2t}} = 51,{26^0} \approx 51,{3^0}\)