Lăng kính là:
Lăng kính là một khối trong suốt, đồng nhất, được giới hạn bởi hai mặt phẳng không song song.
Chọn câu đúng
A, B, C - đúng
Một tia sáng tới gặp mặt bên của một lăng kính dưới góc tới i1 khúc xạ vào lăng kính và ló ra ở mặt bên còn lại. Nếu ta tăng góc i1 thì:
\(D = {i_1} + {i_2} - A = {i_1} + {i_2} - ({r_1} + {r_2})\)
Mặt khác: \(\sin {i_1} = n\sin {r_1};{\rm{ }}\sin {i_2} = n\sin {r_2}\)
=>Góc lệch D có thể tăng hay giảm
Chiếu một tia sáng đến lăng kính thì thấy tia ló ra là một tia sáng đơn sắc. Có thể kết luận tia sáng chiếu tới lăng kính là ánh sáng:
Chùm ánh sáng trắng khi đi qua lăng kính sẽ bị phân tích thành nhiều chùm sáng đơn sắc khác nhau do chiết suất của chất làm lăng kính đối với mỗi ánh sáng khác nhau là khác nhau.
=>Chiếu một tia sáng đến lăng kính thì thấy tia ló ra là một tia sáng đơn sắc => Ánh sáng đó là ánh sáng đơn sắc.
Góc lệch của tia sáng khi truyền qua lăng kính là góc tạo bởi:
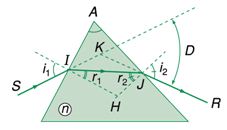
Góc lệch D: là góc tạo bởi tia tới lăng kính và tia ló ra khỏi lăng kính
Một lăng kính bằng thuỷ tinh chiết suất n, góc chiết quang A. Tia sáng tới một mặt bên có thể ló ra khỏi mặt bên thứ hai khi
Ta có: Điều kiện để có tia ló ra cạnh bên:
+ Đối với góc chiết quang A: \(A \le 2{i_{gh}}\)
+ Đối với góc tới i: \(i \ge {i_0}\) với \(\sin {i_0} = n\sin (A - {i_{gh}})\)
Phát biểu nào sau đây là đúng?
Ta có: Khi tia sáng qua lăng kính có góc lệch cực tiểu thì đường đi của tia sáng đối xứng qua mặt phân giác của góc chiết quang của lăng kính.
Ta có:
+ \({i_1} = {i_2} = {i_m}\) (góc tới ứng với độ lệch cực tiểu)
+ \({r_1} = {r_2} = \frac{A}{2}\)
+ \({D_m} = 2{i_m} - A\)
+ \(\sin \frac{{{D_m} + A}}{2} = n\sin \frac{A}{2}\)
Chọn câu trả lời sai
A, C, D - đúng
B- sai vì: Khi ánh sáng truyền từ môi trường có chiết suất lớn hơn chiết suất của lăng kính thì tia ló sẽ lệch về phía đỉnh
Sử dụng hình vẽ về đường đi của tia sáng qua lăng kính: SI là tia tới, JR là tia ló, D là góc lệch giữa tia tới và tia ló, n là chiết suất của chất làm lăng kính. Công thức nào trong các công thức sau là sai?
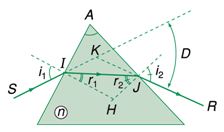
\(\begin{array}{l}\sin {i_1} = n\sin {r_1};{\rm{ }}\sin {i_2} = n\sin {r_2}\\{r_1} + {r_2} = A\\D = {i_1} + {i_2} - A\end{array}\)
+ Khi góc lệch cực tiểu: \(\sin \frac{{{D_m} + A}}{2} = n\sin \frac{A}{2}\)
=> A - sai
Sử dụng hình vẽ về đường đi của tia sáng qua lăng kính: SI là tia tới, JR là tia ló, D là góc lệch giữa tia tới và tia ló, n là chiết suất của chất làm lăng kính.Công thức nào trong các công thức sau đây là đúng?
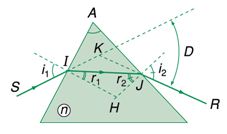
\(\begin{array}{l}\sin {i_1} = n\sin {r_1};{\rm{ }}\sin {i_2} = n\sin {r_2}\\{r_1} + {r_2} = A\\D = {i_1} + {i_2} - A\end{array}\)
+ Khi góc lệch cực tiểu: \(\sin \frac{{{D_m} + A}}{2} = n\sin \frac{A}{2}\)
=> A, B, C đều đúng
Điều nào sau đây là đúng khi nói về lăng kính và đường đi của một tia sáng qua lăng kính?
A- sai vì tiết diện thẳng của lăng kính có thể là tam giác cân có thể làm tam giác thường, có thể là tam giác vuông , ...
B- đúng
C- sai vì không phải mọi tia sáng qua lăng kính đều cho tia ló ra khỏi lăng kính
Điều nào sau đây là đúng khi nói về lăng kính?
A - đúng
B- sai vì: góc chiết quang A có thể lớn hơn 900
C - sai vì: chỉ có lăng kính tam giác cân hoặc tam giác đều thì hai mặt bên của lăng kính mới đối xứng nhau qua mặt phân giác cảu góc chiết quang
D - sai
Lăng kính phản xạ toàn phần là một khối lăng trụ thủy tinh có tiết diện thẳng là:
Lăng kính phản xạ toàn phần là lăng kính thủy tinh có tiết diện thẳng là một tam giác vuông cân
Với i1 , i2 , A lần lượt là góc tới, góc ló và góc chiết quang của lăng kính.Công thức xác định góc lệch D của tia sáng qua lăng kính là:
Góc lệch D của tia sáng qua lăng kính được xác định bởi biểu thức:
\(D = {i_1} + {i_2} - A\)
Một lăng kính có góc chiết quang A. Chiếu tia sáng SI đến vuông góc với mặt bên của lăng kính. Biết góc lệch của tia ló và tia tới là \(D = {15^0}\). Cho chiết suất của lăng kính là \(n = 1,5\). Góc chiết quang A bằng:
Vì chiếu tia tới vuông góc với mặt nên \({i_1} = 0 \to {r_1} = 0\)
Ta có: \(A = {r_1} + {r_2} \to A = {r_2}\)
Mà: \(D = {i_1} + {i_2} - A \leftrightarrow 15 = 0 + {i_2} - A \to {i_2} = 15 + A\)
Lại có:
\(\begin{array}{l}\sin {i_2} = n{\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_2} \leftrightarrow \sin {i_2} = n\sin A \leftrightarrow \sin (15 + A) = 1,5\sin A\\ \leftrightarrow \sin 15c{\rm{osA + sinAcos15 = 1,5sin}}A\\ \leftrightarrow sin15c{\rm{osA = (1,5 - cos15)sinA}}\\ \to \tan A = \frac{{\sin 15}}{{1,5 - c{\rm{os15}}}} = 0,485 \to A = 25,{87^0}\end{array}\)
Một lăng kính có chiết suất \(n = \sqrt 2 \). Chiếu một tia sáng đơn sắc vào mặt bên của lăng kính góc tới \(i = {45^0}\), tia ló ra khỏi lăng kính vuông góc với mặt bên thứ 2 như hình vẽ. Góc chiết quang A của lăng kính:
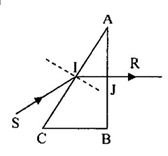
Áp dụng định luật khúc xạ ánh sáng tại điểm tới I của mặt thứ nhất, ta có:
\(\sin {i_1} = n{\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_1} \leftrightarrow \sin 45 = \sqrt 2 {\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_1} \to {\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_1} = \frac{1}{2} \to {r_1} = {30^0}\)
Vì tia ló ra khỏi mặt thứ 2 đi vuông góc nên: \({i_2} = 0 \to {r_2} = 0\)
Ta có: \(A = {r_1} + {r_2} = 30 + 0 = {30^0}\)
Chiếu một tia sáng đơn sắc đến mặt bên AB của một lăng kính tiết diện là một tam giác đều ABC theo phương song song với đáy BC. Tia ló ra khỏi AC đi là là mặt AC. Chiết suất của chất làm lăng kính là:
Vì ∆ABC là tam giác đều và tia tới đi song song với cạnh đáy BC nên dễ suy ra được \({i_1} = {30^0}\).
Mà: \(\sin {i_1} = n{\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_1} \leftrightarrow \sin {30^0} = n{\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_1} \to n{\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_1} = 0,5\) (1)
Tia ló đi là là mặt AC, nên \({i_2} = {90^0}\)
Góc chiết quang: \(A = {r_1} + {r_2}\)
Ta lại có:
\(\begin{array}{l}\sin {i_2} = n{\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_2} \leftrightarrow \sin 90 = n\sin (A - {r_1})\\ \leftrightarrow \sin 90 = n\sin (60 - {r_1}){\rm{ (2)}}\end{array}\)
Lấy (2) chia cho (1) ta được:
\(\begin{array}{l}\frac{{\sin 90}}{{0,5}} = \frac{{n\sin (60 - {r_1})}}{{n{\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_1}}} \leftrightarrow 2{{\mathop{\rm sinr}\nolimits} _1} = sin(60 - {r_1})\\ \leftrightarrow 2\sin {r_1} = \sin 60c{\rm{os}}{{\rm{r}}_1} - c{\rm{os60}}{\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_1}\\ \leftrightarrow (2 + c{\rm{os60)}}{\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_1} = \sin 60.c{\rm{os}}{{\rm{r}}_1}\\ \to {\mathop{\rm t}\nolimits} {\rm{an}}{{\rm{r}}_1} = \frac{{\sin 60}}{{2 + c{\rm{os60}}}} = \frac{{\sqrt 3 }}{5} \to {r_1} = 19,{1^0}\end{array}\)
Thay vào (1), ta được: \(n = \frac{{0,5}}{{{\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_1}}} = \frac{{0,5}}{{{\mathop{\rm s}\nolimits} {\rm{in19,}}{{\rm{1}}^0}}} = 1,53\)
Chiếu một tia sáng SI đến vuông góc với màn E tại I. Trên đường đi của tia sáng, người ta đặt tại đỉnh A của một lăng kính thủy tinh có góc chiết quang \(A = {5^0}\) , chiết suất \(n = 1,5\) sao cho SI vuông góc với mặt phân giác của góc chiết quang A, tia sáng ló đến màn E tại điểm J. Đoạn IJ =?Biết rằng màn E đặt cách đỉnh A của lăng kính một khoảng 1m.
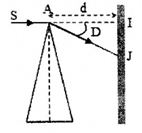
Vì góc chiết quang nhỏ nên ta dễ suy ra công thức tính góc lệch giữa tia tới và tia ló là:
\(D = (n - 1)A\)
Từ hình vẽ, ta có:
\(\tan D = \frac{{{\rm{IJ}}}}{{AI}}\)
Vì A nhỏ, nên D nhỏ
Ta có: \(\tan D \approx D\)
$ \leftrightarrow (n - 1)A = \frac{{IJ}}{{AI}} = \frac{{{\text{IJ}}}}{d} \to I{\text{J}} = d(n - 1)A = 1.(1,5 - 1).\frac{{5.\pi }}{{180}} = 0,0436m = 4,36cm$
Khi chiếu tia sáng đơn sắc màu vàng vào mặt bên của lăng kính có góc chiết quang \(A = {60^0}\) dưới góc tới i1 thì tia ló ra khỏi mặt AC lệch về đáy và cho góc lệch cực tiểu. Nếu thay ánh sáng màu vàng bằng ánh sáng màu đỏ thì góc lệch giữa tia tới và tia ló là bao nhiêu? Biết chiết suất của chất làm lăng kính đối với tia vàng và tia đỏ lần lượt là \({n_V} = 1,52;{n_d} = 1,49\)
Khi tia màu vàng cho góc lệch cực tiểu, ta có:
\(\left\{ \begin{array}{l}{i_{1v}} = {i_{2v}} = i\\{r_{1v}} = {r_{2v}} = \frac{A}{2} = {30^0}\end{array} \right.\)
Áp dụng định luật khúc xạ, ta có: \(\sin i = {n_v}{{\mathop{\rm sinr}\nolimits} _{1v}} = 1,52.\sin {30^0} = 0,76 \to i = {49,46^0}\)
+ Khi thay bằng tia đỏ:
\(\begin{array}{l}\sin i = {n_d}{{\mathop{\rm sinr}\nolimits} _{1d}} \to {{\mathop{\rm sinr}\nolimits} _{1d}} = \frac{{\sin {{49,46}^0}}}{{{n_d}}} = 0.51 \to {r_{1{\rm{d}}}} = {30,67^0}\\A = {r_{1{\rm{d}}}} + {r_{2{\rm{d}}}} \to {r_{2{\rm{d}}}} = A - {r_{1{\rm{d}}}} = 60 - 30,67 = {29,33^0}\\\sin {i_{2{\rm{d}}}} = n{\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_{2{\rm{d}}}} = 1,49.\sin 29,33 = 0,73 \to {i_{2{\rm{d}}}} = {46,87^0}\\D = i + {i_{2{\rm{d}}}} - A = 49,46 + 46,87 - 60 = {36,33^0}\end{array}\)
Một lăng kính có tiết diện thẳng là một tam giác đều ABC. Chiếu 1 chùm sáng trắng hẹp vào mặt bên AB đi lên từ đáy. Chiết suất của lăng kính với ánh sáng đỏ là \(\sqrt 2 \) đối với màu tím là \(\sqrt 3 \). Giả sử ban đầu lăng kính ở vị trí mà tia tím truyền đối xứng qua lăng kính. Ta cần phải quay lăng kính một góc bằng bao nhiêu để tia ló màu đỏ truyền đối xứng qua lăng kính?
Vì tia tím truyền đối xứng qua lăng kính nên ta có: góc lệch D cực tiểu
\(\left\{ \begin{array}{l}{i_{1t}} = {i_{2t}} = i\\{r_{1t}} = {r_{2t}} = \frac{A}{2} = {30^0}\end{array} \right. \to {D_m} = 2i - A \to i = \frac{{{D_m} + 60}}{2}\)
Mặt khác, ta có:
\(\begin{array}{l}\sin i = {n_t}{\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_{1t}} \leftrightarrow \sin \left( {\frac{{{D_m} + 60}}{2}} \right) = \sqrt 3 \sin {30^0}\\ \to \sin \left( {\frac{{{D_m} + 60}}{2}} \right) = \frac{{\sqrt 3 }}{2} \to \frac{{{D_m} + 60}}{2} = 60 \to {D_m} = {60^0},i = {60^0}\end{array}\)
+ Tia ló đỏ truyền đối xứng qua lăng kính thì:
\(\left\{ \begin{array}{l}{i_{1{\rm{d}}}} = {i_{2{\rm{d}}}} = i'\\{r_{1{\rm{d}}}} = {r_{2{\rm{d}}}} = \frac{A}{2} = {30^0}\end{array} \right. \to {D_m} = 2i' - A \to i' = \frac{{{D_m} + 60}}{2}\)
Mặt khác, ta có:
\(\begin{array}{l}\sin i = {n_d}{\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_{1d}} \leftrightarrow \sin \left( {\frac{{{D_m} + 60}}{2}} \right) = \sqrt 2 \sin {30^0}\\ \to \sin \left( {\frac{{{D_m} + 60}}{2}} \right) = \frac{{\sqrt 2 }}{2} \to \frac{{{D_m} + 60}}{2} = 45 \to {D_m} = {30^0},i = {45^0}\end{array}\)
Vậy ta cần phải quay góc: \(\alpha = i - i' = 60 - 45 = {15^0}\)

