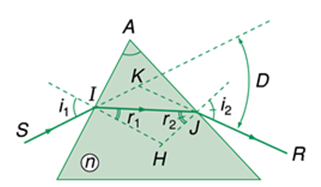
Chiếu một tia sáng đơn sắc đến mặt bên AB của một lăng kính tiết diện là một tam giác đều ABC theo phương song song với đáy BC. Tia ló ra khỏi AC đi là là mặt AC. Chiết suất của chất làm lăng kính là:

Vì ∆ABC là tam giác đều và tia tới đi song song với cạnh đáy BC nên dễ suy ra được \({i_1} = {30^0}\).

Mà: \(\sin {i_1} = n{\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_1} \leftrightarrow \sin {30^0} = n{\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_1} \to n{\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_1} = 0,5\) (1)

Tia ló đi là là mặt AC, nên \({i_2} = {90^0}\)

Góc chiết quang: \(A = {r_1} + {r_2}\)

Ta lại có:

\(\begin{array}{l}\sin {i_2} = n{\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_2} \leftrightarrow \sin 90 = n\sin (A - {r_1})\\ \leftrightarrow \sin 90 = n\sin (60 - {r_1}){\rm{         (2)}}\end{array}\)

Lấy (2) chia cho (1) ta được:

\(\begin{array}{l}\frac{{\sin 90}}{{0,5}} = \frac{{n\sin (60 - {r_1})}}{{n{\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_1}}} \leftrightarrow 2{{\mathop{\rm sinr}\nolimits} _1} = sin(60 - {r_1})\\ \leftrightarrow 2\sin {r_1} = \sin 60c{\rm{os}}{{\rm{r}}_1} - c{\rm{os60}}{\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_1}\\ \leftrightarrow (2 + c{\rm{os60)}}{\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_1} = \sin 60.c{\rm{os}}{{\rm{r}}_1}\\ \to {\mathop{\rm t}\nolimits} {\rm{an}}{{\rm{r}}_1} = \frac{{\sin 60}}{{2 + c{\rm{os60}}}} = \frac{{\sqrt 3 }}{5} \to {r_1} = 19,{1^0}\end{array}\)

Thay vào (1), ta được: \(n = \frac{{0,5}}{{{\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_1}}} = \frac{{0,5}}{{{\mathop{\rm s}\nolimits} {\rm{in19,}}{{\rm{1}}^0}}} = 1,53\)