Chiếu một tia sáng dưới một góc tới 250 vào một lăng kính đặt trong không khí có có góc chiết quang 500 và chiết suất 1,4. Góc lệch của tia sáng qua lăng kính là
Áp dụng các công thức lăng kính ta có:
\(\left\{ \begin{array}{l}
\sin i = n\sin r \Rightarrow \sin {25^0} = 1,4.\sin r \Rightarrow r = {17^0}34'\\
\sin i' = n.\sin r' \Rightarrow \sin i' = 1,4.\sin ({32^0}26') \Rightarrow i' = {48^0}39'\\
A = r + r' \Rightarrow r' = A - r = {50^0} - {17^0}34' = {32^0}26'\\
D = i + i' - A = {25^0} + {48^0}39' - {50^0} = {23^0}29'
\end{array} \right.\)
Phát biểu nào dưới đây không chính xác:
Chiếu một chùm tia sáng vào một mặt bên của một lăng kính ở trong không khí:
+ Đáp án A, B và D đúng:
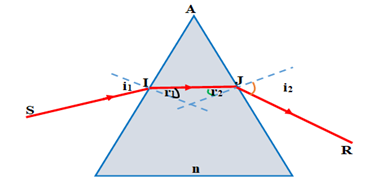

+ Đáp án C sai:
Chiếu một chùm tia sáng vào một mặt bên của một lăng kính ở trong không khí, nếu góc tới r2 tại mặt bên thứ hai lớn hơn igh thì không có tia ló ở mặt bên thứ hai → Phát biểu ở đáp án C không chính xác.
Lăng kính thủy tinh có tiết diện thẳng là tam giác cân ABC đỉnh A. Một tia đơn sắc được chiếu vuông góc tới mặt bên AB. Sau hai lần phản xạ toàn phần trên hai mặt AC và AB, tia ló ra khỏi đáy BC theo phương vuông góc với BC. Tính góc chiết quang A:
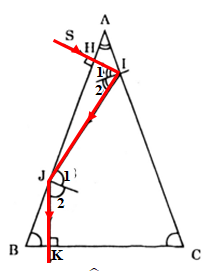
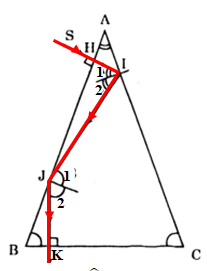
+ Ta có: \(SI \bot AB \Rightarrow \) Tia SI truyền thẳng vào môi trường trong suốt ABC mà không bị khúc xạ.
+ Góc tới mặt AC là: \(\widehat {{I_1}} = \widehat {{I_2}} = \widehat A\)
+ Mặt khác SI song song với pháp tuyến tại J \( \Rightarrow \widehat {{J_1}} = \widehat {{J_2}} = \widehat {SIJ} = 2.\widehat {{I_1}} = 2.\widehat A\)
+ Vì \(JK \bot BC \Rightarrow \widehat B = \widehat {{J_2}} = \widehat {{J_1}} = 2.\widehat A\)
+ Tam giác ABC cân tại A \( \Rightarrow \widehat B = \widehat C = 2.\widehat A\)
+ Tổng 3 góc trong tam giác ACB bằng:
\(\widehat A + \widehat B + \widehat C = {180^0} \Leftrightarrow \widehat A + 2.\widehat A + 2.\widehat A = {180^0} \Rightarrow \widehat A = {36^0}\)
Cho tia sáng truyền tới lăng kính như hình vẽ. Tia ló truyền đi đi sát mặt BC. Chiết suất n của lăng kính có giá trị nào sau đây? (Tính tròn với 1 chữ số thập phân)
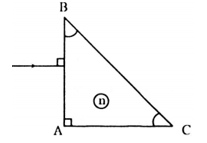
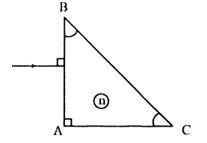
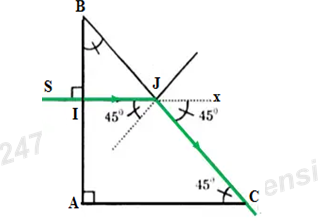

Ta có ΔABC vuông cân \( \Rightarrow \widehat B = \widehat C = {45^0}\)
\(SI \bot AB \Rightarrow \) Tia SI truyền thẳng vào môi trường trong suốt ABC mà không bị khúc xạ
→ Góc tới ở mặt AB là i1 = 0 và góc khúc xạ r1 = 0
Góc tới mặt BC là:\({r_2} = {90^0} - \widehat {BJI} = {90^0} - {45^0} = {45^0}\)
Tia ló truyền sát mặt BC → Góc ló i2 = 900
Áp dụng định luật khúc xạ ánh sáng ta có:
\(n.\sin {r_2} = \sin {i_2} \Rightarrow n = \dfrac{{\sin {i_2}}}{{\sin {r_2}}} = \dfrac{{\sin 90}}{{\sin 45}} = 1,4\)
Một lăng kính có chiết suất n, đặt trong không khí, có góc chiết quang A, nhận một tia sáng tới vuông góc với mặt bên AB và tia ló sát mặt bên AC của lăng kính. Chiết suất n của lăng kính xác định bởi
Theo đề bài ta có i = 00, i’ = 900
Sini1 = nsinr1 => r1= 0 => r2 = A
Sini2 = nsinr2 = nsinA => n = \(\frac{1}{\sin A}\)
Chiếu một chùm tia sáng đỏ hẹp coi như một tia sáng vào mặt bên của một lăng kính có tiết diện thẳng là tam giác cân \(ABC\) có góc chiết quang \(A = {8^0}\) theo phương vuông góc với mặt phẳng phân giác của góc chiết quang tại một điểm tới rất gần \(A\), biết chiết suất của lăng kính đối với tia đỏ là \({n_d}\; = 1,5\). Góc lệch của tia ló so với tia tới là:
Góc lệch của tia ló so với tia tới là:
\(D = \left( {n - 1} \right)A = \left( {1,5 - 1} \right){.8^0} = {4^0}\)

