Câu hỏi:
2 năm trước
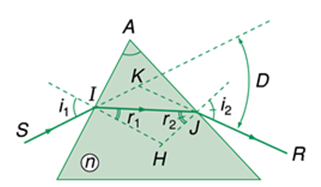
Một lăng kính thủy tinh có chiết suất \(n = \sqrt 2 \). Tiết diện thẳng của lăng kính là một tam giác đều ABC. Chiếu một tia sáng nằm trong mặt phẳng của tiết diện thẳng, tới AB với góc tới \({i_1} = {45^0}\). Góc lệch D của lăng kính có giá trị là:
Trả lời bởi giáo viên
Đáp án đúng: c
+ Áp dụng định luật khúc xạ ánh sáng tại I, ta có:
\(\begin{array}{l}\sin {i_1} = n\sin {r_1}\\ \Leftrightarrow \sin {45^0} = \sqrt 2 {\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_1}\\ \Rightarrow {\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_1} = \dfrac{1}{2} \Rightarrow {r_1} = {30^0}\end{array}\)
+ Lại có góc chiết quang
\(\begin{array}{l}A = {60^0} = {r_1} + {r_2}\\ \Rightarrow {r_2} = A - {r_1} = {60^0} - {30^0} = {30^0}\end{array}\)
+ Áp dụng định luật khúc xạ ánh sáng tại J, ta có:
\(\begin{array}{l}\sin {i_2} = n\sin {r_2}\\ \Leftrightarrow \sin {i_2} = \sqrt 2 \sin {30^0} = \dfrac{{\sqrt 2 }}{2}\\ \Rightarrow {i_2} = {45^0}\end{array}\)
+ Góc lệch của lăng kính: \(D = {i_1} + {i_2} - A = {45^0} + {45^0} - {60^0} = {30^0}\)
Hướng dẫn giải:
Sử dụng các công thức lăng kính
