Câu hỏi:
2 năm trước
Chọn phương án đúng. Một tia sáng tới vuông góc với mặt AB của một lăng kính có chiết suất \(n = \sqrt 2 \) và góc ở đỉnh A = 300, B là góc vuông. Góc lệch của tia sáng qua lăng kính là:
Trả lời bởi giáo viên
Đáp án đúng: c
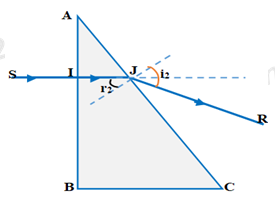
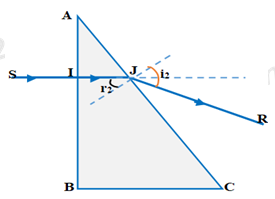
Tia tới: \(SI \bot AB \Rightarrow {i_1} = 0 \Rightarrow {r_1} = 0\)
Góc tới mặt AC: \({r_2} = \widehat A = {30^0}\)
Áp dụng định luật khúc xạ ánh sáng ta có:
\(n.\sin \,{r_2} = \sin {i_2} \Rightarrow \sin {i_2} = \sqrt 2 .\sin 30 = \dfrac{{\sqrt 2 }}{2} \Rightarrow {i_2} = {45^0}\)
Góc lệch của tia sáng qua lăng kính là:
\(D = {i_1} + {\rm{ }}{i_2} - {\rm{ }}A = 0 + {45^0} - {30^0} = {15^0}\)
Hướng dẫn giải:
+ Định luật khúc xạ ánh sáng: \({n_1}\sin i = {n_2}\sin \,r\)
+ Góc lệch: \(D = {i_1} + {i_2} - A\)