Câu hỏi:
2 năm trước
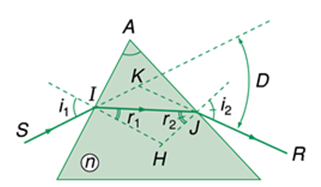
Một lăng kính đặt trong không khí, có góc chiết quang \(A = {30^0}\) nhận một tia sáng tới vuông góc với mặt bên \(AB\) và tia ló sát mặt bên \(AC\) của lăng kính. Chiết suất \(n\) của lăng kính
Trả lời bởi giáo viên
Đáp án đúng: d
Tia tới vuông góc với mặt bên \(AB\) và tia ló sát mặt bên \(AC\)\( \Rightarrow \left\{ \begin{array}{l}{i_1} = {0^0}\\{i_2} = {90^0}\end{array} \right.\)
Áp dụng công thức lăng kính, ta có:
\(\begin{array}{l}\sin {i_1} = n\sin {r_1} \Rightarrow \sin {r_1} = \dfrac{{\sin {i_1}}}{n} = \dfrac{{\sin {0^0}}}{n} = 0 \Rightarrow {r_1} = {0^0}\\ \Rightarrow {r_2} = A - {r_1} = {30^0} - {0^0} = {30^0}\end{array}\)
\(\sin {i_2} = n\sin {r_2} \Rightarrow n = \dfrac{{\sin {i_2}}}{{\sin {r_2}}} = \dfrac{{\sin {{90}^0}}}{{\sin {{30}^0}}} = 2\)
Hướng dẫn giải:
Công thức lăng kính: \(\left\{ \begin{array}{l}\sin {i_1} = n\sin {r_1};\,\,sin{i_2} = n\sin {r_2}\\{r_1} + {r_2} = A\\D = {i_1} + {i_2} - A\end{array} \right.\)
Công thức lượng giác: \(\sin \left( {a + b} \right) = \sin a\cos b + \sin b\cos a\)
