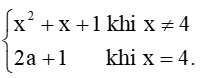Giải SGK Toán 11 Bài 3 (Cánh diều): Hàm số liên tục

48 lượt xem

Bài trước

Bài sau

Chúng tôi giới thiệu Giải bài tập Toán lớp 11 Bài 3: Hàm số liên tục chi tiết sách Toán 11 Tập 1 Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 11. Mời các bạn đón xem:

Giải bài tập Toán lớp 11 Bài 3: Hàm số liên tục

Câu hỏi khởi động trang 73 Toán 11 Tập 1: Cầu sông Hàn là một trong những cây cầu bắc qua sông Hàn ở Đà Nẵng. Đây là cây cầu đầu tiên do kĩ sư, công nhân Việt Nam tự thiết kế và thi công. Khi cầu không quay (Hình 10a), mặt cầu liền mạch nên các phương tiện có thể đi lại giữa hai đầu cầu. Khi cầu quay (Hình 10b) để các tàu, thuyền có thể đi qua thì mặt cầu không còn liền mạch nữa, các phương tiện không thể đi qua giữa hai đầu cầu.

Kiến thức gì trong toán học thể hiện chuyển động có đường đi là đường liền mạch?

Câu hỏi khởi động trang 73 Toán 11 Tập 1 | Cánh diều Giải Toán 11

Lời giải:

Kiến thức trong toán học thể hiện chuyển động của đường đi là đường liên mạch đó là kiến thức về hàm số liên tục.

Để tìm hiểu kĩ hơn hàm số liên tục là gì thì chúng ta sẽ cùng tìm hiểu bài học ngày hôm nay. Bài học: “Hàm số liên tục”.

I. Khái niệm

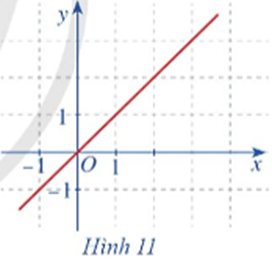
Hoạt động 1 trang 73 Toán 11 Tập 1: Quan sát đồ thị hàm số f(x) = x ở Hình 11.

Hoạt động 1 trang 73 Toán 11 Tập 1 | Cánh diều Giải Toán 11

a) Tính $\lim_{x \to 1}$ f(x).

b) So sánh $\lim_{x \to 1}$ f(x)và f(1).

Lời giải:

a) Ta có: $\lim_{x \to 1} f (x) = \lim_{x \to 1} x$ = 1.

b) Ta có: f(1) = 1 nên $\lim_{x \to 1}$ f(x)=f(1).

Luyện tập 1 trang 74 Toán 11 Tập 1: Xét tính liên tục của hàm số f(x) = x³ + 1 tại x₀ = 1.

Lời giải:

Ta có: $\lim_{x \to 1} f (x) = \lim_{x \to 1} (x^{3} + 1)$ = 2và f(1) = 1³ + 1 = 2

Suy ra $\lim_{x \to 1}$ f(x)=f(1).

Vì vậy hàm số liên tục tại x₀ = 1.

Hoạt động 2 trang 74 Toán 11 Tập 1: Cho hàm số f(x) = x + 1 với x ∈ ℝ.

a) Giả sử x₀ ∈ ℝ. Hàm= số f(x) có liên tục tại điểm x₀ hay không?

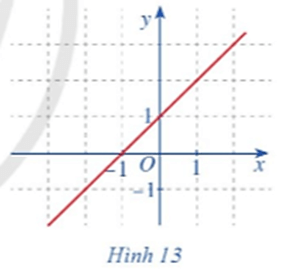
b) Quan sát đồ thị hàm số f(x) = x + 1 với x ∈ ℝ (Hình 13), nêu nhận xét về đặc điểm của đồ thị hàm số đó.

Hoạt động 2 trang 74 Toán 11 Tập 1 | Cánh diều Giải Toán 11

Lời giải:

a) Với x₀ ∈ ℝ bất kì ta có: $\lim_{x \to x_{0}}$ f(x) = x_o+1 - f(x_o). Do đó hàm số liên tục tại x = x₀.

b) Dựa vào đồ thị hàm số ta thấy: Đồ thị hàm số là một đường thẳng liền mạch với mọi giá trị x ∈ ℝ.

Luyện tập 2 trang 75 Toán 11 Tập 1: Hàm số f(x) = 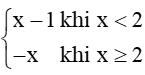. Có liên tục trên ℝ hay không?

Lời giải:

+) Với mỗi x₀ ∈ (– ∞; 2) có $\lim_{x \to x_{0}} f (x) = \lim_{x \to x_{0}} (x - 1) = x_{0} - 1 = f (x_{0})$ là hàm số liên tục.

+) Với mỗi x₀ ∈ (2; +∞) có $\lim_{x \to x_{0}} f (x) = \lim_{x \to x_{0}} (- x) = - x_{0} = f (x_{0})$ là hàm số liên tục.

+) Tại x = 2, ta có: $\lim_{x \to 2} f (x) = \lim_{x \to 2}$ (x-1) = 1và f(2) = – 2 nên $\lim_{x \to 2} f (x) \neq f (2)$ .

Vậy hàm số không liên tục tại x = 2.

II. Một số định lí cơ bản

Hoạt động 3 trang 75 Toán 11 Tập 1: Quan sát đồ thị các hàm số: y = x² – 4x + 3 (Hình 14a); y = $\frac{x + 1}{x - 1} (x \neq 1)$ (Hình 14b); y = tanx (Hình 14c) và nêu nhận xét về tính liên tục của mỗi hàm số đó trên từng khoảng của tập xác định.

Hoạt động 3 trang 75 Toán 11 Tập 1 | Cánh diều Giải Toán 11

Lời giải:

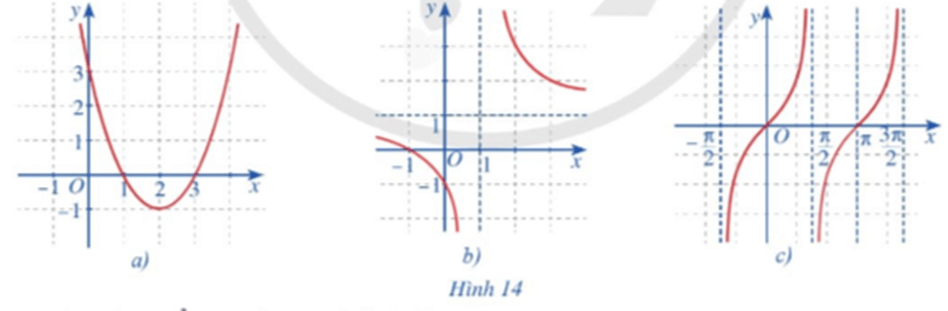
Hình 14a) đồ thị là đường cong Parabol liền mạch nên hàm số liên tục trên toàn bộ khoảng xác định.

Hình 14b) đồ thị bị chia làm hai nhánh:

- Với x < 1 ta thấy hàm số là một đường cong liền nên liên tục.

- Với x > 1 ta thấy hàm số là một đường cong liền nên liên tục.

Vậy hàm đố liên tục trên từng khoảng xác định.

Hình 14c) đồ thị hàm số y = tanx chia thành nhiều nhánh, và mỗi nhánh là các đường cong liền. Do đó hàm số liên tục trên mỗi khoảng xác định của chúng.

Luyện tập 3 trang 76 Toán 11 Tập 1: Hàm f(x)= $\frac{x + 2}{x - 8}$ có liên tục trên mỗi khoảng (– ∞; 8), (8; + ∞) hay không?

Lời giải:

Do f(x)= $\frac{x + 2}{x - 8}$ nên hàm số liên tục trên mỗi khoảng (– ∞; 8), (8; + ∞).

Hoạt động 4 trang 76 Toán 11 Tập 1: Cho hai hàm số f(x)= x³ + x và g(x) = x² + 1 (x ∈ ℝ). Hãy cho biết:

a) Hai hàm số f(x), g(x) có liên tục tại x = 2 hay không.

b) Các hàm số f(x) + g(x); f(x) – g(x); f(x).g(x); $\frac{f (x)}{g (x)}$ có liên tục tại x = 2 hay không.

Lời giải:

a) Tại x = 2 có $\lim_{x \to 2} f (x) = \lim_{x \to 2} (x^{3} + x)$ = 2³+2 = 10 = f(2). Do đó hàm số f(x) liên tục tại x = 2.

Tại x = 2 có $\lim_{x \to 2} g (x) = \lim_{x \to 2} (x^{2} + 1)$ = 2²+1 = 5 = g(2). Do đó hàm số g(x) liên tục tại x = 2.

b) Tại x = 2 có $\lim_{x \to 2} (f (x) + g (x)) = \lim_{x \to 2} f (x) + \lim_{x \to 2} f (x) = 10 + 5 = 15 = f (2) + g (2)$

Do đó hàm số f(x) + g(x) liên tục tại x = 2.

Tại x = 2 có $\lim_{x \to 2} (f (x) - g (x)) = \lim_{x \to 2} f (x) - \lim_{x \to 2} g (x) = 10 - 5 = 5 = f (2) - g (2)$

Do đó hàm số f(x) – g(x) liên tục tại x = 2.

Tại x = 2 có $\lim_{x \to 2} (f (x) . g (x)) = \lim_{x \to 2} f (x) . \lim_{x \to 2} g (x) = 10.5 = 50 = f (2) . g (2)$

Do đó hàm số f(x).g(x) liên tục tại x = 2.

Tại x = 2 có $\lim_{x \to 2} (\frac{f (x)}{g (x)}) = \frac{\lim_{x \to 2} f (x)}{\lim_{x \to 2} g (x)} = \frac{10}{5} = 2 = \frac{f (2)}{g (2)}$

Do đó hàm số $\frac{f (x)}{g (x)}$ liên tục tại x = 2.

Luyện tập 4 trang 76 Toán 11 Tập 1: Xét tính liên tục của hàm số f(x) = sinx + cosx trên ℝ.

Lời giải:

Hàm số sinx và cosx liên tục trên ℝ.

Do đó hàm số y = sinx + cosx liên tục trên ℝ.

Bài tập

Bài 1 trang 77 Toán 11 Tập 1: Dùng định nghĩa xét tính liên tục của hàm số f(x) = 2x³ + x + 1 tại điểm x = 2.

Lời giải:

Hàm số f(x) = 2x³ + x + 1 xác định trên ℝ.

Ta có: $\lim_{x \to 2} f (x) = \lim_{x \to 2} (2 x^{3} + x + 1)$ = 2.2³+2+1 = 17 = f(2).

Do đó hàm số liên tục tại x = 2.

Bài 2 trang 77 Toán 11 Tập 1: Trong các hàm số có đồ thị ở Hình 15a, 15b, 15c, hàm số nào liên tục trên tập xác định của hàm số đó? Giải thích.

Bài 2 trang 77 Toán 11 Tập 1 | Cánh diều Giải Toán 11

Lời giải:

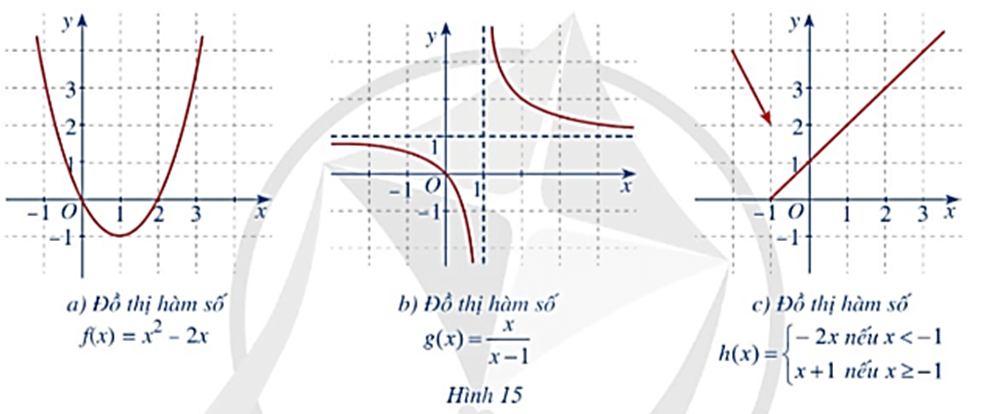
+) Hình 15a): Hàm số f(x) = x² – 2x có tập xác định D = ℝ.

Hàm số liên tục trên toàn bộ ℝ.

+) Hình 16b): Hàm số g(x)= $\frac{x}{x - 1}$ có tập xác định D = ℝ\{1}.

Do đó hàm số liên tục trên từng khoảng xác định của hàm số.

+) Hình 16c):

Với x ∈ (– ∞; – 1) có f(x) = – 2x liên tục.

Với x ∈ (– 1; ∞) có f(x) = x + 1 liên tục.

Tại x = – 1 có $\lim_{x \to - 1} f (x) = \lim_{x \to - 1} 2 x = - 2$ và f(– 1) = – 1 + 1 = 0.

Suy ra $\lim_{x \to - 1} f (x) \neq$ f(-1). Do đó hàm số liên tục tại x = – 1.

Vậy hàm số kiên tục trên các khoảng (– ∞; – 1) và (– 1; ∞).

Bài 3 trang 77 Toán 11 Tập 1: Bạn Nam cho rằng: “Nếu hàm số y = f(x) liên tục tại điểm x₀, còn hàm số y = g(x) không liên tục tại x₀, thì hàm số y = f(x) + g(x) không liên tục tại x₀”. Theo em, ý kiến của bạn Nam đúng hay sai? Giải thích.

Lời giải:

Theo em ý kiến của bạn Nam là đúng.

Ta có: Hàm số y = f(x) liên tục tại điểm x₀ nên $\lim_{x \to x_{0}} f (x) = f (x_{0})$ .

Hàm số y = g(x) không liên tục tại x₀ nên $\lim_{x \to x_{0}} g (x) \neq g (x_{0})$ .

Do đó $\lim_{x \to x_{0}} (f (x) + g (x)) = \lim_{x \to x_{0}} f (x) + \lim_{x \to x_{0}} g (x) \neq f (x_{0}) + g (x_{0})$ .

Vì vậy hàm số không liên tục tại x₀.

Bài 4 trang 77 Toán 11 Tập 1: Xét tính liên tục của mỗi hàm số sau trên tập xác định của hàm số đó:

a) f(x) = x² + sinx;

b) g(x) = x⁴ – x² + $\frac{6}{x - 1}$ ;

c) h(x) = $\frac{2 x}{x - 3} + \frac{x - 1}{x + 4}$ .

Lời giải:

a) Hàm số f(x) = x² + sinx có tập xác định là ℝ.

Hàm số x² và sinx liên tục trên ℝ nên hàm số f(x) = x² + sinx liên tục trên ℝ.

b) Hàm số g(x) = x⁴ – x² + $\frac{6}{x - 1}$ có tập xác định là ℝ\{1}.

Hàm số x⁴ – x² liên tục trên toàn bộ tập xác định

Hàm số $\frac{6}{x - 1}$ liên tục trên các khoảng ( – ∞; 1) và (1; +∞).

Vậy hàm số đã cho liên tục trên từng khoảng xác định của hàm số.

c) Hàm số h(x) = $\frac{2 x}{x - 3} + \frac{x - 1}{x + 4}$ có tập xác định D = ℝ\{– 4; 3}.

Hàm số $\frac{2 x}{x - 3}$ liên tục trên các khoảng ( – ∞; 3) và (3; +∞).

Hàm số $\frac{x - 1}{x + 4}$ liên tục trên các khoảng ( – ∞; – 4) và (– 4; +∞).

Bài 5 trang 77 Toán 11 Tập 1: Cho hàm số f(x) = Bài 5 trang 77 Toán 11 Tập 1 | Cánh diều Giải Toán 11

a) Với a = 0, xét tính liên tục của hàm số tại x = 4.

b) Với giá trị nào của a thì hàm số liên tục tại x = 4?

c) Với giá trị nào của a thì hàm số liên tục trên tập xác định của nó?

Lời giải:

a) Với a = 0, tại x = 4, ta có:

$\lim_{x \to 4} f (x) = \lim_{x \to 4} (x^{2} + x + 1) = 4^{2}$ +4+1 = 21 và f(4) = 2.0 + 1 = 1

Suy ra $\lim_{x \to 4} f (x) \neq f (4)$ .

Vì vậy hàm số không liên tục tại x = 4.

b) Ta có: $\lim_{x \to 4} f (x) = \lim_{x \to 4} (x^{2} + x + 1) = 4^{2}$ +4+1 = 21và f(4) = 2.a + 1

Để hàm số liên tục tại x = 4 thì $\lim_{x \to 4}$ f(x) = f(4)

⇔ 21 = 2a + 1

⇔ 2a = 20

⇔ a = 10

Vậy với a = 10 thì hàm số liên tục tại x = 4.

c) Với x ∈ (– ∞; 4) có f(x) = x² + x + 1 liên tục với mọi x thuộc khoảng này.

Với x ∈ (4; +∞) có f(x) = 2a + 1 liên tục với mọi x thuộc khoảng này.

Tại x = 4 thì a = 10 hàm số liên tục.

Vậy với a = 10 hàm số liên tục trên tập xác định của nó.

Bài 6 trang 77 Toán 11 Tập 1: Hình 16 biểu thị độ cao h(m) của một quả bóng đá lên theo thời gian t(s), trong đó h(t) = – 2t² + 8t.

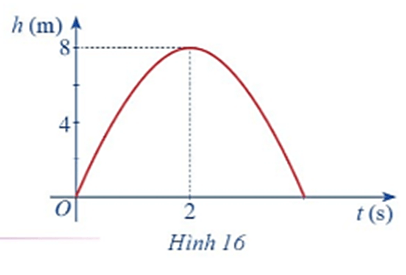
a) Chứng tỏ hàm số h(t) liên tục trên tập xác định.

b) Dựa vào đồ thị hãy xác định $\lim_{t \to 2} (- 2 t^{2} + 8 t)$ .

Bài 6 trang 77 Toán 11 Tập 1 | Cánh diều Giải Toán 11

Lời giải:

a) Hàm số h(t) = – 2t² + 8t là hàm đa thức nên liên tục trên tập xác định.

b) Dựa vào đồ thị hàm số khi t tiến dần đế 2 thì h(t) dần đến 8.

Vậy $\lim_{t \to 2} (- 2 t^{2} + 8 t) = 8$ .

Xem thêm các bài giải SGK Toán lớp 11 Cánh diều hay, chi tiết khác:

Bài 2: Giới hạn của hàm số

Bài 3: Hàm số liên tục

Bài tập cuối chương 3

Xem thêm các chương trình khác:

Bài trước

Bài sau

Giải SGK, SBT, Chuyên đề Toán Học Lớp 11 Sách cánh diều