Hai đèn sáng như thế nào biết công suất định mức của mỗi đèn là 6W.
Hiệu điện thế định mức của mỗi đèn :
\({U_{dm}} = \sqrt {{P_{dm}}.{R_D}} \, = \,\sqrt {6.6\,} \, = \,6V\).
Mà \({U_V} = {\rm{ }}3V < {U_{dm}}\) nên đèn sáng mờ hơn.
Tìm điện trở mỗi đèn.
Suất điện động và điện trở trong của bộ nguồn :
\({E_b} = E = 16V\) và \({r_b} = \frac{r}{2}\, = \,1\Omega \)
- Cường độ dòng điện qua mạch chính :
\(I\, = \,\frac{{{E_b}}}{{{R_1} + {R_{D12}} + {R_2} + {r_b}}}\, = \,\frac{{16}}{{13 + \frac{{{R_D}}}{2}}}\)
Mặt khác, ta có :
\(I = \,\frac{{{U_V}}}{{{R_{D12}}}}\, = \,\frac{3}{{\frac{{{R_D}}}{2}}} \to {R_D} = 6\Omega \)
Tìm điện trở mỗi đèn.
Suất điện động và điện trở trong của bộ nguồn :
\({E_b} = E = 16V\) và \({r_b} = \frac{r}{2}\, = \,1\Omega \)
- Cường độ dòng điện qua mạch chính :
\(I\, = \,\frac{{{E_b}}}{{{R_1} + {R_{D12}} + {R_2} + {r_b}}}\, = \,\frac{{16}}{{13 + \frac{{{R_D}}}{2}}}\)
Mặt khác, ta có :
\(I = \,\frac{{{U_V}}}{{{R_{D12}}}}\, = \,\frac{3}{{\frac{{{R_D}}}{2}}} \to {R_D} = 6\Omega \)
Hai điện trở mắc song song vào nguồn điện nếu \({R_1} < {R_2}\) và \({R_{12}}\) là điện trở tương đương của hệ mắc song song.
Phương án nào sau đây sai.
Ta có:
+ \(\dfrac{1}{{{R_{//}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} \to {R_{12}} = {R_{//}} < {R_1},{R_2}\)
+ \({U_1} = {U_2} \leftrightarrow {I_1}{R_1} = {I_2}{R_2} \to {I_1} = \dfrac{{{R_2}}}{{{R_1}}}{I_2} > {I_2}\) (do \({R_2} > {R_1}\) )
+ Công suất tiêu thụ: \(P = {I^2}R \to \left\{ \begin{array}{l}{P_1} = I_1^2{R_1} = \dfrac{{R_2^2}}{{{R_1}}}I_2^2 = \dfrac{{{R_2}}}{{{R_1}}}{P_2}\\{P_2} = I_2^2{R_2}\end{array} \right. \to {P_1} > {P_2}\)
(do \({R_2} > {R_1}\) )
- Cách khác:
Ta có: \(P = \dfrac{{{U^2}}}{R}\) => P tỉ lệ nghịch với điện trở R
\({R_2} > {R_1} \to {P_2} < {P_1}\)
Ta suy ra:
A, B, C – đúng
D - sai
Chọn phương án sai.
Khi một tải R nối vào nguồn suất điện động \(\xi \) và điện trở trong r, thấy công suất mạch ngoài cực đại thì:
Công suất mạch ngoài : \(P = {R_N}{I^2} = {\rm{ }}{R_N}.{\left( {\dfrac{E}{{{R_N} + r}}} \right)^2}\, = \,\dfrac{{{E^2}}}{{{{\left( {\sqrt {{R_N}} + \dfrac{r}{{\sqrt {{R_N}} }}} \right)}^2}}}\)
Để \(P = {P_{Max}}\) thì \(\left( {\sqrt {{R_N}} + \dfrac{r}{{\sqrt {{R_N}} }}} \right)\) nhỏ nhất.
Theo BĐT Cô-si thì : \(\left( {\sqrt {{R_N}} + \dfrac{r}{{\sqrt {{R_N}} }}} \right)\; \ge 2\sqrt r \)
Dấu “=” xảy ra khi \(\sqrt {{R_N}} \, = \,\dfrac{r}{{\sqrt {{R_N}} }}\,\, \Rightarrow \,{R_N}\, = \,r\)
Khi đó: \(P = {P_{{\rm{max}}}} = \dfrac{{{E^2}}}{{4r}}\)
=> Phương án D – sai vì: \(I = \dfrac{E}{{2r}} = \dfrac{E}{{2R}}\)
Một bóng đèn sáng bình thường ở hiệu điện thế \(220V\) số chỉ ampe kế trong mạch là \(341mA\). Trong 30 ngày, bóng tiêu thụ hết bao nhiêu tiền? Biết mỗi ngày trung bình đèn thắp sắng trong 4 giờ và giá điện là \(2500\) đ/số.
Ta có,
+ Hiệu điện thế định mức của đèn: \({U_d} = 220V\)
+ Cường độ dòng điện định mức: \({I_d} = 341mA\)
+ Công suất của đèn: \(P = UI = {220.341.10^{ - 3}} = 75,02W\)
Thời gian sử dụng đèn: \(t = 4.30 = 120h\)
+ Điện năng tiêu thụ: \(W = Pt = 75,02.120 = 9002,4{\rm{W}}h = 9,0024kWh\)
Ta có \(1kWh = 1\) số và có giá \(2500\)đ
Ta suy ra, bóng tiêu thụ hết số tiền trong 30 ngày là: \(9,0024.2500 = 22506\) đ
Tính điện năng tiêu thụ của ấm trong \(30\) ngày mỗi ngày \(20\) phút theo đơn vị \(kWh\)
- Đổi các đơn vị:
+ \(t = 10p = 10.60 = 600s\)
+ \(H = 90\% = 0,9\)
+ \({m_{nuoc}} = D.V = {1000.1,5.10^{ - 3}} = 1,5kg\)
- Nhiệt lượng tỏa ra: \({Q_1} = UIt = \dfrac{{{U^2}}}{R}t\)
- Nhiệt lượng thu vào: \({Q_2} = mc\Delta t = mc\left( {{t_2} - {t_1}} \right)\)
Ta có:
Hiệu suất \(H=\dfrac{Q_2}{Q_1}\), suy ra:
\(\begin{array}{l}H{Q_1} ={Q_2} \Leftrightarrow H\dfrac{{{U^2}}}{R}t = mc\left( {{t_2} - {t_1}} \right)\\ \Leftrightarrow 0,9\dfrac{{{{220}^2}}}{R}.600 = 1,5.4200\left( {100 - 20} \right)\\ \Rightarrow R = 51,9 ≈ 52\Omega \end{array}\)
+ Công suất của ấm: \(P = \dfrac{{{U^2}}}{R} = \dfrac{{{{220}^2}}}{{52}} = 930,77W\)
\(t = 20p = \dfrac{1}{3}h\)
+ Điện năng tiêu thụ của ấm trong 30 ngày mỗi ngày 20 phút là: \({\rm{W}} = Pt = 930,77.\dfrac{1}{3}.30 = 9307,7Wh = 9,3kWh\)
Tính điện trở của ấm
- Đổi các đơn vị:
+ \(t = 10p = 10.60 = 600s\)
+ \(H = 90\% = 0,9\)
+ \({m_{nuoc}} = D.V = {1000.1,5.10^{ - 3}} = 1,5kg\)
- Nhiệt lượng tỏa ra: \({Q_1} = UIt = \dfrac{{{U^2}}}{R}t\)
- Nhiệt lượng thu vào: \({Q_2} = mc\Delta t = mc\left( {{t_2} - {t_1}} \right)\)
Ta có:
Hiệu suất \(H=\dfrac{Q_2}{Q_1}\), suy ra:
\(\begin{array}{l}H{Q_1} ={Q_2} \Leftrightarrow H\dfrac{{{U^2}}}{R}t = mc\left( {{t_2} - {t_1}} \right)\\ \Leftrightarrow 0,9\dfrac{{{{220}^2}}}{R}.600 = 1,5.4200\left( {100 - 20} \right)\\ \Rightarrow R = 51,9≈52\Omega \end{array}\)
Tính điện trở của ấm
- Đổi các đơn vị:
+ \(t = 10p = 10.60 = 600s\)
+ \(H = 90\% = 0,9\)
+ \({m_{nuoc}} = D.V = {1000.1,5.10^{ - 3}} = 1,5kg\)
- Nhiệt lượng tỏa ra: \({Q_1} = UIt = \dfrac{{{U^2}}}{R}t\)
- Nhiệt lượng thu vào: \({Q_2} = mc\Delta t = mc\left( {{t_2} - {t_1}} \right)\)
Ta có:
Hiệu suất \(H=\dfrac{Q_2}{Q_1}\), suy ra:
\(\begin{array}{l}H{Q_1} ={Q_2} \Leftrightarrow H\dfrac{{{U^2}}}{R}t = mc\left( {{t_2} - {t_1}} \right)\\ \Leftrightarrow 0,9\dfrac{{{{220}^2}}}{R}.600 = 1,5.4200\left( {100 - 20} \right)\\ \Rightarrow R = 51,9≈52\Omega \end{array}\)
Công suất tỏa nhiệt trên \({R_2}\)
+ Ta có \({R_A}nt{R_3}nt[{R_1}//{R_2}{\rm{]}}\)
\(\dfrac{1}{{{R_{12}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} \Rightarrow {R_{12}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\)
Điện trở tương đương của toàn mạch:
\(\begin{array}{l}{R_{td}} = {R_A} + {R_3} + {R_{12}} = {R_A} + {R_3} + \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\\ = 0,2 + 3,8 + \dfrac{{24.{R_2}}}{{24 + {R_2}}} = 4 + \dfrac{{24{R_2}}}{{24 + {R_2}}}\end{array}\)
Lại có \({R_{td}} = \dfrac{U}{I} = \dfrac{{12}}{1} = 12\Omega \)
Thay lên trên, ta được:
\(\begin{array}{l}4 + \dfrac{{24{R_2}}}{{24 + {R_2}}} = 12\\ \Rightarrow {R_2} = 12\Omega \end{array}\)
\( \Rightarrow {R_{12}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} = \dfrac{{24.12}}{{24 + 12}} = 8\Omega \)
+ Ta có \({U_{12}} = I.{R_{12}} = 1.8 = 8V\)
Do \({R_1}//{R_2} \Rightarrow {U_1} = {U_2} = {U_{12}}\)
+ Công suất tỏa nhiệt trên \({R_2}\): \({P_2} = \dfrac{{U_2^2}}{{{R_2}}} = \dfrac{{{8^2}}}{{12}} = \dfrac{{16}}{3}{\rm{W}}\)
Nhiệt lượng tỏa ra trên \({R_1}\) trong thời gian \(5\) phút
+ Ta có \({R_A}nt{R_3}nt[{R_1}//{R_2}{\rm{]}}\)
\(\dfrac{1}{{{R_{12}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} \Rightarrow {R_{12}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\)
Điện trở tương đương của toàn mạch:
\(\begin{array}{l}{R_{td}} = {R_A} + {R_3} + {R_{12}} = {R_A} + {R_3} + \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\\ = 0,2 + 3,8 + \dfrac{{24.{R_2}}}{{24 + {R_2}}} = 4 + \dfrac{{24{R_2}}}{{24 + {R_2}}}\end{array}\)
Lại có \({R_{td}} = \dfrac{U}{I} = \dfrac{{12}}{1} = 12\Omega \)
Thay lên trên, ta được:
\(\begin{array}{l}4 + \dfrac{{24{R_2}}}{{24 + {R_2}}} = 12\\ \Rightarrow {R_2} = 12\Omega \end{array}\)
\( \Rightarrow {R_{12}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} = \dfrac{{24.12}}{{24 + 12}} = 8\Omega \)
+ Ta có \({U_{12}} = I.{R_{12}} = 1.8 = 8V\)
Do \({R_1}//{R_2} \Rightarrow {U_1} = {U_2} = {U_{12}}\)
Ta suy ra, nhiệt lượng tỏa ra trên \({R_1}\) là: \({Q_1} = I_1^2{R_1}t = \dfrac{{U_1^2}}{{{R_1}}}t = \dfrac{{{8^2}}}{{24}}.5.60 = 800J\)
Điện trở \({R_2}\)
+ Ta có \({R_A}nt{R_3}nt[{R_1}//{R_2}{\rm{]}}\)
\(\dfrac{1}{{{R_{12}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} \Rightarrow {R_{12}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\)
Điện trở tương đương của toàn mạch:
\(\begin{array}{l}{R_{td}} = {R_A} + {R_3} + {R_{12}} = {R_A} + {R_3} + \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\\ = 0,2 + 3,8 + \dfrac{{24.{R_2}}}{{24 + {R_2}}} = 4 + \dfrac{{24{R_2}}}{{24 + {R_2}}}\end{array}\)
Lại có \({R_{td}} = \dfrac{U}{I} = \dfrac{{12}}{1} = 12\Omega \)
Thay lên trên, ta được:
\(\begin{array}{l}4 + \dfrac{{24{R_2}}}{{24 + {R_2}}} = 12\\ \Rightarrow {R_2} = 12\Omega \end{array}\)
Điện trở \({R_2}\)
+ Ta có \({R_A}nt{R_3}nt[{R_1}//{R_2}{\rm{]}}\)
\(\dfrac{1}{{{R_{12}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} \Rightarrow {R_{12}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\)
Điện trở tương đương của toàn mạch:
\(\begin{array}{l}{R_{td}} = {R_A} + {R_3} + {R_{12}} = {R_A} + {R_3} + \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\\ = 0,2 + 3,8 + \dfrac{{24.{R_2}}}{{24 + {R_2}}} = 4 + \dfrac{{24{R_2}}}{{24 + {R_2}}}\end{array}\)
Lại có \({R_{td}} = \dfrac{U}{I} = \dfrac{{12}}{1} = 12\Omega \)
Thay lên trên, ta được:
\(\begin{array}{l}4 + \dfrac{{24{R_2}}}{{24 + {R_2}}} = 12\\ \Rightarrow {R_2} = 12\Omega \end{array}\)
Công suất tiêu thụ trên biến trở là lớn nhất, tính công suất đó.
Đặt \({R_x} = x\)
Ta có: \({U_{DB}} = U - {U_{AD}} = U - IR\)
Lại có: \(I = \dfrac{U}{{R + \dfrac{{{R_D}x}}{{{R_D} + x}}}}\)
Suy ra: \({U_{DB}} = U - \dfrac{{UR}}{{R + \dfrac{{{R_D}x}}{{{R_D} + x}}}} = 9 - \dfrac{{9.4}}{{4 + \dfrac{{12x}}{{12 + x}}}} = \dfrac{{27x}}{{12 + 4x}} = \dfrac{{27x}}{{4\left( {3 + x} \right)}}\)
\( \Rightarrow {P_x} = \dfrac{{U_{DB}^2}}{{{R_x}}} = \dfrac{{{{\left( {\dfrac{{27x}}{{4\left( {3 + x} \right)}}} \right)}^2}}}{x} = \dfrac{{729}}{{16{{\left( {\dfrac{3}{{\sqrt x }} + \sqrt x } \right)}^2}}}\)
\({\left[ {{P_x}} \right]_{max}}\) khi \({\left( {\dfrac{3}{{\sqrt x }} + \sqrt x } \right)_{\min }}\)
Theo BDT Cosi ta có: \(\left( {\dfrac{3}{{\sqrt x }} + \sqrt x } \right) \ge 2\sqrt {\dfrac{3}{{\sqrt x }}\sqrt x } = 2\sqrt 3 \)
Dấu xảy ra khi \(\dfrac{3}{{\sqrt x }} = \sqrt x \Rightarrow x = 3\Omega \)
Vậy với \({R_x} = x = 3\Omega \) thì công suất tiêu thụ trên biến trở là lớn nhất \({P_{{x_{{\rm{max}}}}}} = 3,8W\)
Đèn sáng bình thường
Ta có, đèn sáng bình thường nên: \({U_{DB}} = {U_{{R_x}}} = {U_D} = 6V\)
\( \Rightarrow I = \dfrac{{{U_{AD}}}}{R} = \dfrac{{{U_{AB}} - {U_{DB}}}}{R} = \dfrac{{9 - 6}}{4} = 0,75A\)
Mặt khác, ta có: \({I_{{R_x}}} = I - {I_D}\)
Lại có \({I_D} = \dfrac{{{P_D}}}{{{U_D}}} = \dfrac{3}{6} = 0,5A\)
Ta suy ra: \({I_{{R_x}}} = I - {I_D} = 0,75 - 0,5 = 0,25A\)
\( \Rightarrow {R_x} = \dfrac{{{U_{BD}}}}{{{I_{{R_x}}}}} = \dfrac{6}{{0,25}} = 24\Omega \)
Đèn sáng bình thường
Ta có, đèn sáng bình thường nên: \({U_{DB}} = {U_{{R_x}}} = {U_D} = 6V\)
\( \Rightarrow I = \dfrac{{{U_{AD}}}}{R} = \dfrac{{{U_{AB}} - {U_{DB}}}}{R} = \dfrac{{9 - 6}}{4} = 0,75A\)
Mặt khác, ta có: \({I_{{R_x}}} = I - {I_D}\)
Lại có \({I_D} = \dfrac{{{P_D}}}{{{U_D}}} = \dfrac{3}{6} = 0,5A\)
Ta suy ra: \({I_{{R_x}}} = I - {I_D} = 0,75 - 0,5 = 0,25A\)
\( \Rightarrow {R_x} = \dfrac{{{U_{BD}}}}{{{I_{{R_x}}}}} = \dfrac{6}{{0,25}} = 24\Omega \)
Cho mạch điện có sơ đồ như hình vẽ:
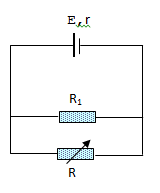
Biết, \(E = 6V,r = 1\Omega ,{R_1} = 4\Omega \), R là biến trở
Tìm R để công suất tiêu thụ trên R là cực đại? Tính giá trị công suất cực đại khi đó?
Ta có: PR = \(\dfrac{{{U^2}}}{R}\)
Mặt khác: \({U_R} = {\rm{ }}I.{R_N} = \dfrac{E}{{\dfrac{{{R_1}.R}}{{{R_1} + R}} + r}}.\dfrac{{{R_1}.R}}{{{R_1} + R}}\, = \,\dfrac{{24R}}{{5R + 4}}\).
Vậy: \({P_R} = \dfrac{{{{24}^2}{R^2}}}{{{{\left( {5R + 4} \right)}^2}.R}}\, = \,\dfrac{{576}}{{{{\left( {5\sqrt R + \dfrac{4}{{\sqrt R }}} \right)}^2}}}\,\)
Theo BĐT Cô-si, ta có : \(\left( {5\sqrt R + \dfrac{4}{{\sqrt R }}} \right)\, \ge \,4\sqrt 5 \), dấu \('' = ''\) xảy ra khi : \(\left( {5\sqrt R = \dfrac{4}{{\sqrt R }}} \right)\) hay \(R = \dfrac{4}{5}\Omega \).
Vậy : \({P_{RMax}} = \dfrac{{576}}{{{{\left( {4\sqrt 5 } \right)}^2}}}\, = 7,2\,{\rm{W}}\) khi \(R = \dfrac{4}{5}\Omega \)
Thay \({R_2}\) bằng một bóng đèn thì đèn sáng bình thường, khi đó công suất trên đoạn mạch AB là lớn nhất. Tính công suất và hiệu điện thế định mức của đèn.
Thay \({R_2}\) bằng đèn, từ hình vẽ ta có:
+ Cường độ dòng điện mạch chính: \(I = \dfrac{U}{{r + {R_{AB}}}}\)
+ Công suất trên AB: \({P_{AB}} = {I^2}{R_{AB}} = \dfrac{{{U^2}{R_{AB}}}}{{{{\left( {r + {R_{AB}}} \right)}^2}}} = \dfrac{{{U^2}}}{{\dfrac{{{r^2}}}{{{R_{AB}}}} + {R_{AB}} + 2r}}\)
+ Theo BĐT Cosi, ta có: \(\dfrac{{{r^2}}}{{{R_{AB}}}} + {R_{AB}} \ge 2r\)
\( \Rightarrow {P_{A{B_{max}}}} = \dfrac{{{U^2}}}{{2r + 2r}} = \dfrac{{{U^2}}}{{4r}}\)
Khi đó \(r = {R_{AB}} = 3\Omega \)
Mặt khác,
\(\begin{array}{l}{R_{AB}} = \dfrac{{{R_1}{R_D}}}{{{R_1} + {R_D}}} = 3\\ \Leftrightarrow \dfrac{{6{R_D}}}{{6 + {R_D}}} = 3 \Rightarrow {R_D} = 6\Omega \end{array}\)
+ Mặt khác, vì \({R_{AB}} = r\) \( \Rightarrow {U_D} = {U_{AB}} = 0,5U = 6V\)
+ Công suất định mức của đèn: \({P_D} = \dfrac{{U_D^2}}{{{R_D}}} = \dfrac{{{6^2}}}{6} = 6W\)
Điều chỉnh biến trở \({R_2}\) để cho công suất trên nó là lớn nhất, khi đó công suất trên \({R_2}\) bằng 3 lần công suất trên \({R_1}\). Tìm \({R_1}\)?
Ta có: \(rnt\left[ {{R_1}//{R_2}} \right]\)
\({R_{AB}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\)
\( \Rightarrow \) Điện trở toàn mạch: \(R = r + {R_{AB}} = r + \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} = \dfrac{{{R_2}\left( {r + {R_1}} \right) + r{R_1}}}{{{R_1} + {R_2}}}\)
+ Dòng điện mạch chính: \(I = \dfrac{U}{R} = \dfrac{{U\left( {{R_1} + {R_2}} \right)}}{{{R_2}\left( {r + {R_1}} \right) + r{R_1}}}\)
+ Từ hình vẽ, ta có: \({U_2} = {U_{AB}} = I.{R_{AB}} = \dfrac{{U{R_1}{R_2}}}{{{R_2}\left( {r + {R_1}} \right) + r{R_1}}}\)
+ Công suất trên \({R_2}\): \({P_2} = \dfrac{{U_2^2}}{{{R_2}}} = \dfrac{{{U^2}R_1^2{R_2}}}{{{{\left[ {{R_2}\left( {r + {R_1}} \right) + r{R_1}} \right]}^2}}} = \dfrac{{{U^2}R_1^2}}{{{{\left[ {\sqrt {{R_2}} \left( {r + {R_1}} \right) + \dfrac{{r{R_1}}}{{\sqrt {{R_2}} }}} \right]}^2}}}\)
Theo BDT Cosi ta có: \(\sqrt {{R_2}} \left( {r + {R_1}} \right) + \dfrac{{r{R_1}}}{{\sqrt {{R_2}} }} \ge 2\sqrt {\left( {r + {R_1}} \right){R_1}} \)
Vậy công suất cực đại trên \({R_2}\) là: \({P_2} = \dfrac{{{U^2}R_1^2}}{{4\left( {r + {R_1}} \right)r{R_1}}} = \dfrac{{{U^2}{R_1}}}{{4\left( {r + {R_1}} \right)r}}\)
Khi \({P_{{2_{max}}}}\) thì \(\sqrt {{R_2}} \left( {r + {R_1}} \right) = \dfrac{{r{R_1}}}{{\sqrt {{R_2}} }} \Rightarrow {R_2} = \dfrac{{r{R_1}}}{{\left( {r + {R_1}} \right)}}\)
\( \Leftrightarrow {R_2} = \dfrac{{3{R_1}}}{{3 + {R_1}}}{\rm{ }}\left( 1 \right)\)
+ Mặt khác, theo đầu bài, ta có: \(\dfrac{{{P_1}}}{{{P_2}}} = \dfrac{1}{3} \Leftrightarrow \dfrac{{\dfrac{{U_{AB}^2}}{{{R_1}}}}}{{\dfrac{{U_{AB}^2}}{{{R_2}}}}} = \dfrac{1}{3}\)
\( \Leftrightarrow \dfrac{{{R_2}}}{{{R_1}}} = \dfrac{1}{3} \Rightarrow {R_1} = 3{R_2}{\rm{ }}\left( 2 \right)\)
Từ (1) và (2) giải ra ta có: \(\left\{ \begin{array}{l}{R_1} = 6\Omega \\{R_2} = 2\Omega \end{array} \right.\)
Điều chỉnh biến trở \({R_2}\) để cho công suất trên nó là lớn nhất, khi đó công suất trên \({R_2}\) bằng 3 lần công suất trên \({R_1}\). Tìm \({R_1}\)?
Ta có: \(rnt\left[ {{R_1}//{R_2}} \right]\)
\({R_{AB}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\)
\( \Rightarrow \) Điện trở toàn mạch: \(R = r + {R_{AB}} = r + \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} = \dfrac{{{R_2}\left( {r + {R_1}} \right) + r{R_1}}}{{{R_1} + {R_2}}}\)
+ Dòng điện mạch chính: \(I = \dfrac{U}{R} = \dfrac{{U\left( {{R_1} + {R_2}} \right)}}{{{R_2}\left( {r + {R_1}} \right) + r{R_1}}}\)
+ Từ hình vẽ, ta có: \({U_2} = {U_{AB}} = I.{R_{AB}} = \dfrac{{U{R_1}{R_2}}}{{{R_2}\left( {r + {R_1}} \right) + r{R_1}}}\)
+ Công suất trên \({R_2}\): \({P_2} = \dfrac{{U_2^2}}{{{R_2}}} = \dfrac{{{U^2}R_1^2{R_2}}}{{{{\left[ {{R_2}\left( {r + {R_1}} \right) + r{R_1}} \right]}^2}}} = \dfrac{{{U^2}R_1^2}}{{{{\left[ {\sqrt {{R_2}} \left( {r + {R_1}} \right) + \dfrac{{r{R_1}}}{{\sqrt {{R_2}} }}} \right]}^2}}}\)
Theo BDT Cosi ta có: \(\sqrt {{R_2}} \left( {r + {R_1}} \right) + \dfrac{{r{R_1}}}{{\sqrt {{R_2}} }} \ge 2\sqrt {\left( {r + {R_1}} \right){R_1}} \)
Vậy công suất cực đại trên \({R_2}\) là: \({P_2} = \dfrac{{{U^2}R_1^2}}{{4\left( {r + {R_1}} \right)r{R_1}}} = \dfrac{{{U^2}{R_1}}}{{4\left( {r + {R_1}} \right)r}}\)
Khi \({P_{{2_{max}}}}\) thì \(\sqrt {{R_2}} \left( {r + {R_1}} \right) = \dfrac{{r{R_1}}}{{\sqrt {{R_2}} }} \Rightarrow {R_2} = \dfrac{{r{R_1}}}{{\left( {r + {R_1}} \right)}}\)
\( \Leftrightarrow {R_2} = \dfrac{{3{R_1}}}{{3 + {R_1}}}{\rm{ }}\left( 1 \right)\)
+ Mặt khác, theo đầu bài, ta có: \(\dfrac{{{P_1}}}{{{P_2}}} = \dfrac{1}{3} \Leftrightarrow \dfrac{{\dfrac{{U_{AB}^2}}{{{R_1}}}}}{{\dfrac{{U_{AB}^2}}{{{R_2}}}}} = \dfrac{1}{3}\)
\( \Leftrightarrow \dfrac{{{R_2}}}{{{R_1}}} = \dfrac{1}{3} \Rightarrow {R_1} = 3{R_2}{\rm{ }}\left( 2 \right)\)
Từ (1) và (2) giải ra ta có: \(\left\{ \begin{array}{l}{R_1} = 6\Omega \\{R_2} = 2\Omega \end{array} \right.\)

