Tính điện năng tiêu thụ trên dây dẫn khi dòng điện không đổi có cường độ 5A chạy qua dây dẫn trong 3 giờ, biết hiệu điện thế giữa hai dây dẫn này là 12V ?
Theo bài ra ta có: \(\left\{ \begin{array}{l}I = 5A\\U = 12V\\t = 3\,\left( h \right) = 10\,800s\end{array} \right.\)
Điện năng tiêu thụ trên dây dẫn là:
\(A = UIt = 12.5.3.60.60 = 648000J\)
Mắc nguồn điện một chiều có điện trở trong r = 1Ω với mạch ngoài là điện trở R = 4 Ω để thành mạch kín. Biết công suất của nguồn là 20 W. Công suất toả nhiệt trên điện trở R là
Ta có tỉ số công suất:
\(\begin{array}{l}\dfrac{P}{{{P_{ng}}}} = \dfrac{{{I^2}R}}{{{I^2}\left( {R + r} \right)}} = \dfrac{R}{{R + r}} \Rightarrow P = {P_{ng}}.\dfrac{R}{{R + r}}\\ \Rightarrow P = 20.\dfrac{4}{{4 + 1}} = 16\,\,\left( {\rm{W}} \right)\end{array}\)
Đề thi THPT QG - 2020
Một nguồn điện một chiều có suất điện động \(\xi \) đang phát điện ra mạch ngoài với dòng điện có cường độ \(I\). Công suất của nguồn điện được tính bằng biểu thức nào sau đây?
Công suất của nguồn điện: \(P = \xi I\)
Cho mạch điện như hình vẽ. Nguồn điện có suất điện động \(E = 9V\) và điện trở trong \(r = 1Ω\). Đèn có ghi \(6V\) – \(3W\). Bỏ qua điện trở của dây nối. Giá trị của biến trở \(R\) để đèn sáng bình thường là
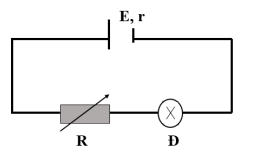
Bóng đèn (6V – 3W) có R = 12Ω và Iđm= 0,5A
Đèn sáng bình thường nên dòng điện qua đèn là I = 0,5A
Áp dụng định luật Ôm cho toàn mạch : \(I = \dfrac{E}{{r + {R_b} + {R_d}}} = 0,5A \Rightarrow \dfrac{9}{{1 + {R_b} + 12}} = 0,5 \Rightarrow {R_b} = 5\Omega \)
Một ấm điện có ghii 120V – 480W, người ta sử dụng nguồn có hiệu điện thế 120V để đun nước. Điện trở của ấm và cường độ dòng điện qua ấm bằng
Ta có:
\(P = \dfrac{{{U^2}}}{R} \Rightarrow R = \dfrac{{{U^2}}}{P} = \dfrac{{{{120}^2}}}{{480}} = 30\Omega \)
Cường độ dòng điện qua ấm là:
\(I = \dfrac{U}{R} = \dfrac{{120}}{{30}} = 4{\rm{A}}\)
Gọi E là suất điện động của nguồn điện, I là cường độ dòng điện qua nguồn, U là hiệu điện thế giữa hai cực của nguồn điện, t là thời gian dòng điện chạy qua. Công suất của nguồn điện được xác định theo công thức:
Công suất của nguồn điện là P = E.I
Một điện trở 10 Ω có dòng điện xoay chiều chạy qua trong thời gian 30 phút thì nhiệt lượng tỏa ra là 900 kJ. Cường độ dòng điện cực đại chạy qua điện trở là
Nhiệt lượng tỏa ra trên điện trở là:
\(\begin{array}{l}Q = {I^2}Rt \Rightarrow I = \sqrt {\frac{Q}{{R.t}}} = \sqrt {\frac{{{{900.10}^3}}}{{10.30.60}}} = \sqrt {50} \,\,\left( A \right)\\ \Rightarrow {I_0} = I\sqrt 2 = 10\,\,\left( A \right)\end{array}\)
Hai điện trở mắc song song vào nguồn điện nếu \({R_1} < {R_2}\) và \({R_{12}}\) là điện trở tương đương của hệ mắc song song thì:
Ta có:
+ \(\frac{1}{{{R_{//}}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}} \to {R_{12}} = {R_{//}} < {R_1},{R_2}\)
+ \({U_1} = {U_2} \leftrightarrow {I_1}{R_1} = {I_2}{R_2} \to {I_1} = \frac{{{R_2}}}{{{R_1}}}{I_2} > {I_2}\) (do \({R_2} > {R_1}\) )
+ Công suất tiêu thụ: \(P = {I^2}R \to \left\{ \begin{array}{l}{P_1} = I_1^2{R_1} = \frac{{R_2^2}}{{{R_1}}}I_2^2 = \frac{{{R_2}}}{{{R_1}}}{P_2}\\{P_2} = I_2^2{R_2}\end{array} \right. \to {P_1} > {P_2}\)
(do \({R_2} > {R_1}\) )
- Cách khác:
Ta có: $P = \frac{{{U^2}}}{R}$ => P tỉ lệ nghịch với điện trở R
${R_2} > {R_1} \to {P_2} < {P_1}$
Hai bóng đèn có công suất định mức là \({P_1} = 25W\), \({P_2} = 100W\) đều làm việc bình thường ở hiệu điện thế \(110V\). Khi mắc nối tiếp hai đèn này vào hiệu điện thế 220V thì:
+ Khi ở hiệu điện thế 110V, hai bóng đèn hoạt động bình thường, ta có:
\(\left\{ \begin{array}{l}{I_{dm1}} = \frac{{{P_1}}}{{110}} = 0,227A\\{I_{dm2}} = \frac{{{P_2}}}{{110}} = 0,91A\end{array} \right.\)
Điện trở của hai bóng đèn: \(\left\{ \begin{array}{l}{R_1} = \frac{{{P_1}}}{{I_1^2}} = 484\Omega \\{R_2} = \frac{{{P_2}}}{{I_2^2}} = 121\Omega \end{array} \right.\)
+ Khi mắc nối tiếp hai đèn vào, điện trở của toàn mạch: \(R = {R_1} + {R_2} = 484 + 121 = 605\Omega \)
Cường độ dòng điện qua hai bóng đèn: \(I = \frac{U}{R} = \frac{{220}}{{605}} = 0,364A\)
Nhận thấy: \(\left\{ \begin{array}{l}I > {I_1}\\I < {I_2}\end{array} \right.\) => đèn 1 quá sáng dễ cháy, đèn 2 sáng yếu
Khi một tải R nối vào nguồn suất điện động \(\xi \) và điện trở trong r, thấy công suất mạch ngoài cực đại thì:
Công suất mạch ngoài : \(P = {R_N}{I^2} = {\rm{ }}{R_N}.{\left( {\dfrac{E}{{{R_N} + r}}} \right)^2}\, = \,\dfrac{{{E^2}}}{{{{\left( {\sqrt {{R_N}} + \dfrac{r}{{\sqrt {{R_N}} }}} \right)}^2}}}\)
Để \(P = {P_{Max}}\) thì \(\left( {\sqrt {{R_N}} + \dfrac{r}{{\sqrt {{R_N}} }}} \right)\) nhỏ nhất.
Theo BĐT Cô-si thì :
\(\left( {\sqrt {{R_N}} + \dfrac{r}{{\sqrt {{R_N}} }}} \right) \ge 2\sqrt r \)
Dấu “=” xảy ra khi \(\sqrt {{R_N}} \, = \,\dfrac{r}{{\sqrt {{R_N}} }}\,\, \Rightarrow \,{R_N}\, = \,r\)
Khi đó: \(P = {P_{{\rm{max}}}} = \dfrac{{{E^2}}}{{4r}}\)
Một đèn ống loại 40 W được chế tạo để có công suất chiếu sáng bằng đèn dây tóc loại 100 W. Hỏi nếu sử dụng đèn ống này trong trung bình mỗi ngày 5 giờ thì trong 30 ngày sẽ giảm được bao nhiêu tiền điện so với sử dụng đèn dây tóc nói trên. Biết giá tiền điện là 700 đ/kWh.
+ Điện năng tiêu thụ khi dùng đèn ống: \({W_1} = {\rm{ }}{P_1}.5.30{\rm{ }} = {\rm{ }}6{\rm{ }}kWh\)
+ Điện năng tiêu thụ khi dùng đèn dây tóc: \({W_2} = {\rm{ }}{P_2}.5.30{\rm{ }} = {\rm{ }}15{\rm{ }}kWh\)
=> Tiền điện giảm được: (W2 – W1).700 đ/kWh = 6300 đ.
Một bàn là điện khi được sử dụng với hiệu điện thế $220 V$ thì dòng điện chạy qua bàn là có cường độ dòng điện là $5 A$. Biết giá tiền điện là $700 đ/kWh$.
Tính nhiệt lượng mà bàn là toả ra trong $20$ phút.
Nhiệt lượng mà bàn là toả ra trong $20$ phút : \(Q = UIt = 220.5.20.60{\rm{ }} = 1320000\left( J \right)\)
Một bàn là điện khi được sử dụng với hiệu điện thế $220 V$ thì dòng điện chạy qua bàn là có cường độ dòng điện là $5 A$. Biết giá tiền điện là $700 đ/kWh$.
Tính tiền điện phải trả cho việc sử dụng bàn là này trong $30$ ngày, mỗi ngày sử dụng $20$ phút ?
\(Q = UIt = 220.5.20.60.30 = 39600000{\rm{ }}\left( J \right) = 11\left( {kWh} \right)\)
=> Tiền điện phải trả: $Q.700 đ/kWh = 7700 đ.$
Cho mạch điện có sơ đồ như hình vẽ :
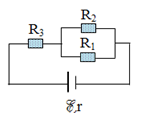
Biết, \(E = 6V,{\rm{ }}r = 2\Omega ,{R_1} = 6\Omega ,{\rm{ }}{R_2} = 12\Omega ,{\rm{ }}{R_3} = 4\Omega \)
Tính cường độ dòng điện chạy qua \({R_1}\)?
+ Ta có: \(\left( {{R_3}nt{\rm{ }}\left( {{R_2}//{R_1}} \right)} \right)\)
\({R_{12}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} = \dfrac{{6.12}}{{6 + 12}} = 4\Omega \)
=> Điện trở tương đương của mạch ngoài là: \(R = {R_3} + {R_{12}} = 4 + 4 = 8\Omega \)
+ Cường độ dòng điện qua mạch chính: \(I = \dfrac{E}{{R + r}} = \dfrac{6}{{8 + 2}} = 0,6A\)
Do \(\left( {{R_3}nt{\rm{ }}\left( {{R_2}//{R_1}} \right)} \right)\), ta suy ra: \(I = {I_3} = {I_{12}} = {I_1} + {I_2}\)
\( \to {I_1} + {I_2} = 0,6A\)
Ta lại có:
\(\begin{array}{l}{U_1} = {U_2} \leftrightarrow {I_1}{R_1} = {I_2}{R_2}\\ \leftrightarrow {I_1}6 = {I_2}12 \to {I_1} = 2{I_2}\end{array}\)
=> Cường độ dòng điện chạy qua \({R_1}\) là: \({I_1} = \dfrac{{0,6}}{{1 + \dfrac{1}{2}}} = 0,4A\)
Cho mạch điện có sơ đồ như hình vẽ :

Biết, \(E = 6V,{\rm{ }}r = 2\Omega ,{R_1} = 6\Omega ,{\rm{ }}{R_2} = 12\Omega ,{\rm{ }}{R_3} = 4\Omega \)
Tính công suất tiêu thụ điện năng trên R3?
Ta có: cường độ dòng điện qua $R_3$ là $I_3 = I =0,6A$
=> Công suất tiêu thụ điện năng trên \({R_3}\) là: \({P_3} = I_3^2.{R_3} = {0,6^2}.4 = 1,44W\)
Cho mạch điện có sơ đồ như hình vẽ :

Biết, \(E = 6V,{\rm{ }}r = 2\Omega ,{R_1} = 6\Omega ,{\rm{ }}{R_2} = 12\Omega ,{\rm{ }}{R_3} = 4\Omega \)
Tính công của nguồn sản ra trong 5 phút?
Ta có cường độ dòng điện $I=0,6A$ (Tính được ở các câu trên)
=> Công của nguồn điện sản ra trong $5$ phút: \(A = EIt = 6.0,6.5.60 = 1080{\rm{ }}J\)
Một nguồn điện có suất điện động \(E = 6{\rm{ }}V\), điện trở trong \(r = 2\Omega \), mạch ngoài có điện trở R.
Tính R để công suất tiêu thụ mạch ngoài là 4W?
Công suất tiêu thụ mạch ngoài: \(P = R.{I^2} = {\rm{ }}R.\dfrac{{{E^2}}}{{{{\left( {R + r} \right)}^2}}}\) khi \(P = 4W\) thì
\(4 = R.\dfrac{{{6^2}}}{{{{\left( {R + 2} \right)}^{2\,}}}}\,\, \to \left[ \begin{gathered}
R = 1\Omega \hfill \\
R = 4\Omega \hfill \\
\end{gathered} \right.\)
Một nguồn điện có suất điện động \(E = 6{\rm{ }}V\), điện trở trong \(r = 2\Omega \), mạch ngoài có điện trở R.
Với giá trị nào của R thì công suất tiêu thụ mạch ngoài lớn nhất?
Ta có: : \(P = R.{I^2} = R.{\left( {\dfrac{E}{{R + r}}} \right)^2}\, = \,\dfrac{{{E^2}}}{{{{\left( {\sqrt R + \dfrac{r}{{\sqrt R }}} \right)}^2}}}\)
Để \(P = {P_{Max}}\) thì \(\left( {\sqrt R + \dfrac{r}{{\sqrt R }}} \right)\) nhỏ nhất.
Theo BĐT Cô-si thì :
\(\left( {\sqrt R + \dfrac{r}{{\sqrt R }}} \right) \ge 2r\)
Dấu “=” xảy ra khi \(\sqrt R \, = \,\dfrac{r}{{\sqrt R }}\,\, \Rightarrow \,{R_N}\, = \,r\, = \,2\Omega \)
Khi đó:
\(P = {P_{Max}} = \dfrac{{{E^2}}}{{4r}} = \dfrac{{{6^2}}}{{4.2}}\, = \,4,5{\rm{W}}\)
Vậy với \(R = 2\Omega \) thì công suất tiêu thụ mạch ngoài lớn nhất.
Cho mạch điện có sơ đồ như hình vẽ:
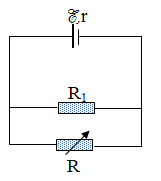
Biết, \(E = 15V,r = 1\Omega ,{R_1} = 2\Omega \), R là biến trở
Tìm R để công suất tiêu thụ trên R là cực đại? Tính giá trị công suất cực đại khi đó?
Ta có: PR = \(\dfrac{{{U^2}}}{R}\)
Mặt khác: \({U_R} = {\rm{ }}I.{R_N} = \dfrac{E}{{\dfrac{{{R_1}.R}}{{{R_1} + R}} + r}}.\dfrac{{{R_1}.R}}{{{R_1} + R}}\, = \,\dfrac{{30R}}{{3R + 2}}\).
Vậy: \({P_R} = \dfrac{{900{R^2}}}{{{{\left( {3R + 2} \right)}^2}.R}}\, = \,\dfrac{{900}}{{{{\left( {3\sqrt R + \dfrac{2}{{\sqrt R }}} \right)}^2}}}\,\)
Theo BĐT Cô-si, ta có : \(\left( {3\sqrt R + \dfrac{2}{{\sqrt R }}} \right)\, \ge \,2\sqrt 6 \), dấu \('' = ''\) xảy ra khi : \(\left( {3\sqrt R = \dfrac{2}{{\sqrt R }}} \right)\) hay \(R=\dfrac{2}{3}\Omega \).
Vậy : \({P_{RMax}} = \dfrac{{900}}{{{{\left( {2\sqrt 6 } \right)}^2}}}\, = \,37,5{\rm{W}}\)
Cho mạch điện có sơ đồ như hình vẽ:
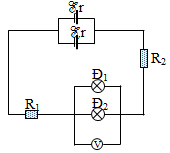
Biết. E = 16 V, r = 2\(\Omega \), R1 = 3\(\Omega \), R2 = 9\(\Omega \).
Đ1 và Đ2 là 2 đèn giống nhau. Vôn kế chỉ 3V, điện trở vôn kế rất lớn.
Tìm điện trở mỗi đèn.
Suất điện động và điện trở trong của bộ nguồn :
\({E_b} = E = 16V\) và \({r_b} = \frac{r}{2}\, = \,1\Omega \)
- Cường độ dòng điện qua mạch chính :
\(I\, = \,\frac{{{E_b}}}{{{R_1} + {R_{D12}} + {R_2} + {r_b}}}\, = \,\frac{{16}}{{13 + \frac{{{R_D}}}{2}}}\)
Mặt khác, ta có :
\(I = \,\frac{{{U_V}}}{{{R_{D12}}}}\, = \,\frac{3}{{\frac{{{R_D}}}{2}}} \to {R_D} = 6\Omega \)

