Cho mạch điện có sơ đồ như hình vẽ:
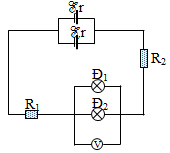
Biết. E = 16 V, r = 2\(\Omega \), R1 = 3\(\Omega \), R2 = 9\(\Omega \).
Đ1 và Đ2 là 2 đèn giống nhau. Vôn kế chỉ 3V, điện trở vôn kế rất lớn.
Hai đèn sáng như thế nào biết công suất định mức của mỗi đèn là 6W.
Hiệu điện thế định mức của mỗi đèn :
\({U_{dm}} = \sqrt {{P_{dm}}.{R_D}} \, = \,\sqrt {6.6\,} \, = \,6V\).
Mà \({U_V} = {\rm{ }}3V < {U_{dm}}\) nên đèn sáng mờ hơn.
Cho mạch điện có sơ đồ như hình vẽ:

Biết. E = 16 V, r = 2\(\Omega \), R1 = 3\(\Omega \), R2 = 9\(\Omega \).
Đ1 và Đ2 là 2 đèn giống nhau. Vôn kế chỉ 3V, điện trở vôn kế rất lớn.
Thay vôn kế bằng 1 ampe kế có Ra = 0. tính cường độ dòng điện qua ampe kế ?
Ta có, khi thay vôn kế bằng ampe kế thì dòng điện không qua 2 đèn mà chỉ qua ampe kế, số chỉ ampe kế lúc này là :
\(I\, = \,\frac{{{E_b}}}{{{R_1} + {R_2} + {r_b}}}\, = \,1,23A\)
Cho mạch điện như hình vẽ:
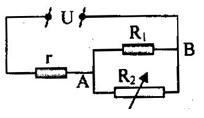
Biết \(r = 3\Omega \), \({R_1},{R_2}\) là một biến trở. \(U = 12V\)
Thay \({R_2}\) bằng một bóng đèn thì đèn sáng bình thường, khi đó công suất trên đoạn mạch AB là lớn nhất. Tính công suất và hiệu điện thế định mức của đèn.
Thay \({R_2}\) bằng đèn, từ hình vẽ ta có:
+ Cường độ dòng điện mạch chính: \(I = \dfrac{U}{{r + {R_{AB}}}}\)
+ Công suất trên AB: \({P_{AB}} = {I^2}{R_{AB}} = \dfrac{{{U^2}{R_{AB}}}}{{{{\left( {r + {R_{AB}}} \right)}^2}}} = \dfrac{{{U^2}}}{{\dfrac{{{r^2}}}{{{R_{AB}}}} + {R_{AB}} + 2r}}\)
+ Theo BĐT Cosi, ta có: \(\dfrac{{{r^2}}}{{{R_{AB}}}} + {R_{AB}} \ge 2r\)
\( \Rightarrow {P_{A{B_{max}}}} = \dfrac{{{U^2}}}{{2r + 2r}} = \dfrac{{{U^2}}}{{4r}}\)
Khi đó \(r = {R_{AB}} = 3\Omega \)
Mặt khác,
\(\begin{array}{l}{R_{AB}} = \dfrac{{{R_1}{R_D}}}{{{R_1} + {R_D}}} = 3\\ \Leftrightarrow \dfrac{{6{R_D}}}{{6 + {R_D}}} = 3 \Rightarrow {R_D} = 6\Omega \end{array}\)
+ Mặt khác, vì \({R_{AB}} = r\) \( \Rightarrow {U_D} = {U_{AB}} = 0,5U = 6V\)
+ Công suất định mức của đèn: \({P_D} = \dfrac{{U_D^2}}{{{R_D}}} = \dfrac{{{6^2}}}{6} = 6W\)
Cho mạch điện như hình vẽ:

Biết \(r = 3\Omega \), \({R_1},{R_2}\) là một biến trở. \(U = 12V\)
Điều chỉnh biến trở \({R_2}\) để cho công suất trên nó là lớn nhất, khi đó công suất trên \({R_2}\) bằng 3 lần công suất trên \({R_1}\). Tìm \({R_1}\)?
Ta có: \(rnt\left[ {{R_1}//{R_2}} \right]\)
\({R_{AB}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\)
\( \Rightarrow \) Điện trở toàn mạch: \(R = r + {R_{AB}} = r + \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} = \dfrac{{{R_2}\left( {r + {R_1}} \right) + r{R_1}}}{{{R_1} + {R_2}}}\)
+ Dòng điện mạch chính: \(I = \dfrac{U}{R} = \dfrac{{U\left( {{R_1} + {R_2}} \right)}}{{{R_2}\left( {r + {R_1}} \right) + r{R_1}}}\)
+ Từ hình vẽ, ta có: \({U_2} = {U_{AB}} = I.{R_{AB}} = \dfrac{{U{R_1}{R_2}}}{{{R_2}\left( {r + {R_1}} \right) + r{R_1}}}\)
+ Công suất trên \({R_2}\): \({P_2} = \dfrac{{U_2^2}}{{{R_2}}} = \dfrac{{{U^2}R_1^2{R_2}}}{{{{\left[ {{R_2}\left( {r + {R_1}} \right) + r{R_1}} \right]}^2}}} = \dfrac{{{U^2}R_1^2}}{{{{\left[ {\sqrt {{R_2}} \left( {r + {R_1}} \right) + \dfrac{{r{R_1}}}{{\sqrt {{R_2}} }}} \right]}^2}}}\)
Theo BDT Cosi ta có: \(\sqrt {{R_2}} \left( {r + {R_1}} \right) + \dfrac{{r{R_1}}}{{\sqrt {{R_2}} }} \ge 2\sqrt {\left( {r + {R_1}} \right){R_1}} \)
Vậy công suất cực đại trên \({R_2}\) là: \({P_2} = \dfrac{{{U^2}R_1^2}}{{4\left( {r + {R_1}} \right)r{R_1}}} = \dfrac{{{U^2}{R_1}}}{{4\left( {r + {R_1}} \right)r}}\)
Khi \({P_{{2_{max}}}}\) thì \(\sqrt {{R_2}} \left( {r + {R_1}} \right) = \dfrac{{r{R_1}}}{{\sqrt {{R_2}} }} \Rightarrow {R_2} = \dfrac{{r{R_1}}}{{\left( {r + {R_1}} \right)}}\)
\( \Leftrightarrow {R_2} = \dfrac{{3{R_1}}}{{3 + {R_1}}}{\rm{ }}\left( 1 \right)\)
+ Mặt khác, theo đầu bài, ta có: \(\dfrac{{{P_1}}}{{{P_2}}} = \dfrac{1}{3} \Leftrightarrow \dfrac{{\dfrac{{U_{AB}^2}}{{{R_1}}}}}{{\dfrac{{U_{AB}^2}}{{{R_2}}}}} = \dfrac{1}{3}\)
\( \Leftrightarrow \dfrac{{{R_2}}}{{{R_1}}} = \dfrac{1}{3} \Rightarrow {R_1} = 3{R_2}{\rm{ }}\left( 2 \right)\)
Từ (1) và (2) giải ra ta có: \(\left\{ \begin{array}{l}{R_1} = 6\Omega \\{R_2} = 2\Omega \end{array} \right.\)
Hai bóng đèn sợi đốt 12 V – 0,6 A và 12 V – 0,3 A mắc đồng thời vào mạch điện một chiều thấy chúng sáng bình thường. Trong 30 phút, điện năng hai bóng đèn tiêu thụ là
Ta có hai đèn sáng bình thường
\( \Rightarrow \) Điện năng hai bóng đèn tiêu thụ trong 30 phút:
\(Q = \left( {{U_1}{I_1} + {U_2}{I_2}} \right)t = \left( {12.0,6 + 12.0,3} \right).30.60 = 19440J\)
Có hai điện trở R1 và R2 (\({R_1} = 2{R_2}\)) mắc nối tiếp với nhau vào hai đầu một đoạn mạch có hiệu điện thế không đổi. Công suất tỏa nhiệt trên điện trở R1 là P1, công suất tỏa nhiệt trên R2 là:
Hai điện trở mắc nối tiếp, công suất tỏa nhiệt trên mỗi điện trở là:
\(\left\{ \begin{array}{l}
{P_1} = {I_1}^2{R_1}\\
{P_2} = {I_2}^2{R_2}\\
{I_1} = {I_2} = I
\end{array} \right. \Rightarrow \dfrac{{{P_2}}}{{{P_1}}} = \dfrac{{{I^2}{R_2}}}{{{I^2}{R_1}}} = \dfrac{{{R_2}}}{{{R_1}}} = \dfrac{1}{2} \Rightarrow {P_2} = \dfrac{1}{2}{P_1}\)
Để loại bóng đèn 120 V – 60 W sáng bình thường ở mạng điện có hiệu điện thế 220 V, người ta mắc nối tiếp với nó điện trở có giá trị là
Cường độ dòng điện định mức của bóng đèn là:
\({I_{dm}} = \dfrac{{{P_{dm}}}}{{{U_{dm}}}} = \dfrac{{60}}{{120}} = 0,5\,\,\left( A \right) = {I_m}\)
Hiệu điện thế trong mạch là: \({U_m} = {U_d} + {U_R} \Rightarrow 220 = 120 + {U_R} \Rightarrow {U_R} = 100\,\,\left( V \right)\)
\( \Rightarrow R = \dfrac{{{U_R}}}{{{I_m}}} = \dfrac{{100}}{{0,5}} = 200\,\,\left( \Omega \right)\)
Giả sử hiệu điện thế đặt vào hai đầu bóng đèn có ghi 220 V – 100W đột ngột tăng lên tới 240 V trong khoảng thời gian ngắn. Hỏi công suất điện của bóng đèn khi đó tăng lên hay giảm đi bao nhiêu phần trăm (%) so với công suất định mức của nó ? Cho rằng điện trở của bóng đèn không thay đổi so với khi hoạt động ở chế độ định mức
Cách giải:
Điện trở của bóng đèn là: \(R = \frac{{{U^2}}}{P} = \frac{{{{220}^2}}}{{100}} = 484\Omega \)
Khi hiệu điện thế tăng lên tới 240V. Công suất của đèn khi đó là:
\(P' = \frac{{U{'^2}}}{R} = \frac{{{{240}^2}}}{{484}} = 119W\)
→ Công suất này tăng 19% so với công suất định mức: P = 19%.Pđm
Hai bóng đèn có công suất định mức lần lượt là 25W và 100W đều làm việc bình thường ở hiệu điện thế 110V. Khi mắc nối tiếp hai bóng đèn này vào mạng điện có hiệu điện thế 220V thì đèn nào sẽ dễ hỏng (cháy)?
Cách giải:
Cường độ dòng điện định mức qua các bóng đèn lần lượt là: \(\left\{ \begin{array}{l}{I_1} = \frac{{{P_1}}}{{{U_1}}} = \frac{5}{{22}}A\\{I_2} = \frac{{{P_2}}}{{{U_2}}} = \frac{{20}}{{22}}A\end{array} \right.\)
Điện trở của các bóng đèn lần lượt là: \(\left\{ \begin{array}{l}{R_1} = \frac{{U_1^2}}{{{P_1}}} = 484\Omega \\{R_2} = \frac{{U_2^2}}{{{P_2}}} = 121\Omega \end{array} \right.\)
Nếu mắc nối tiếp hai bóng đèn này vào mạng điện có hiệu điện thế 220V thì cường độ dòng điện qua mạch là: \(I = \frac{U}{{{R_1} + {R_2}}} = \frac{{220}}{{484 + 121}} = \frac{8}{{22}}A\)
Ta thấy: I1 < I < I2 nên đèn (1) sẽ dễ hỏng (cháy).
Một nguồn điện có suất điện động 12V. Khi mắc nguồn điện này thành mạch điện kín thì nó cung cấp một dòng điện có cường độ 0,8A. Tính công của nguồn điện này sản ra trong thời gian 15 phút và tính công suất của nguồn điện khi đó.
Ta có: E = 12; I = 0,8A
Công của nguồn điện sinh ra trong 15 phút:
Ang = E.I.t = 12.0,8.15.60 = 8640J
Công suất của nguồn điện khi này:
Png = E.I = 12.0,8 = 9,6W
Trên nhãn của một ấm điện có ghi 220V - 1000W. Sử ấm điện với hiệu điện thế 220V để đun sôi 2 lít nước từ nhiệt độ 250C. Tính thời gian đun nước, biết hiệu suất của ấm nước là 90% và nhiệt dung riêng của nước là 4190J/kg.K
Nhiệt lượng cần thiết để làm sôi 2l nước:
\(Q = m.c.\Delta t = 2.4190.\left( {100 - 25} \right) = 628500J\)
Hiệu suất của ấm nước là 90% : \(H = \dfrac{Q}{A}.100\% = 90\% \)
→ Điện năng thực tế mà ấm đã tiêu thụ: \(A = \dfrac{Q}{H} = P.t \Rightarrow t = \dfrac{Q}{{H.P}} = \dfrac{{628500}}{{0,9.1000}} \approx 698,3s\)
Đặt vào hai đầu điện trở \(R\) một hiệu điện thế không đổi \(U\). Công suất toả nhiệt trên điện trở \(R\) là
Công suất toả nhiệt trên \(R:\,\,P = {I^2}R = \frac{{{U^2}}}{R}.\)
Điện năng tiêu thụ được đo bằng.
Điện năng tiêu thụ được đo bằng công tơ điện.
Một bóng đèn trên vỏ có ghi 220V – 50W. Điện trở định mức của đèn là
Ta có:
\(\left\{ \begin{array}{l}U = 220V\\P = 50W\end{array} \right.;P = \dfrac{{{U^2}}}{R} \Rightarrow R = \dfrac{{{U^2}}}{P} = \dfrac{{{{220}^2}}}{{50}} = 968\Omega \)
Một bóng đèn có ghi \(D\left( {3V-3W} \right)\). Khi đèn sáng bình thường, điện trở có giá trị là
Điện trở của bóng đèn là: \(R = \dfrac{{{U_{dm}}^2}}{{{P_{dm}}}} = \dfrac{{{3^2}}}{3} = 3\,\,\left( W \right)\)
Biết rằng điện trở mạch ngoài của một nguồn điện tăng từ \({R_1} = 3\,\,\Omega \) đến \({R_2} = 10,5\,\,\Omega \) thì hiệu suất của nguồn tăng gấp \(2\) lần. Điện trở trong của nguồn bằng
Khi điện trở mạch ngoài là \({R_1};\,\,{R_2}\), hiệu suất của nguồn điện là: \(\left\{ \begin{array}{l}{H_1} = \dfrac{{{R_1}}}{{{R_1} + r}}\\{H_2} = \dfrac{{{R_2}}}{{{R_2} + r}}\end{array} \right.\)
Theo đề bài ta có:
\({H_2} = 2{H_1} \Rightarrow \dfrac{{{R_2}}}{{{R_2} + r}} = 2\dfrac{{{R_1}}}{{{R_1} + r}} \Rightarrow \frac{{10,5}}{{10,5 + r}} = \dfrac{{2.3}}{{3 + r}} \Rightarrow r = 7\,\,\left( \Omega \right)\)
Hai dây dẫn đồng chất có cùng chiều dài nhưng khác tiết diện (S2 = 2S1) được mắc nối tiếp vào một mạch điện. Trong cùng một thời gian thì nhiệt lượng tỏa ra trên hai dây liên hệ với nhau qua biểu thức
Ta có:
\(\left\{ \begin{array}{l}{R_1} = \rho \dfrac{l}{{{S_1}}}\\{R_2} = \rho \dfrac{l}{{2{S_1}}}\end{array} \right. \Rightarrow {R_1} = 2{{\rm{R}}_2}\)
Do \({R_1}nt{R_2}\) nên \(I = {I_1} = {I_2}\)
\( \Rightarrow \left\{ \begin{array}{l}{Q_1} = {I^2}{R_1}t\\{Q_2} = {I^2}\dfrac{{{R_1}}}{2}t\end{array} \right. \Rightarrow {Q_1} = 2{Q_2}\)
Cho mạch điện như hình vẽ (a), \({R_1} = {R_2} = 40\Omega ;{R_3} = 20\Omega \). Đặt vào hai điểm AB hiệu điện thế U thì hiệu điện thế giữa hai đầu điện trở R3 là U3 = 60 V. Công suất tỏa nhiệt trên điện trở R1 là
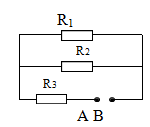
Ta có:
\({R_1}//{R_2}//{R_3} \Rightarrow \left\{ \begin{array}{l}U = {U_1} = {U_2} = {U_3} = 60V\\I = {I_1} + {I_2} + {I_3}\end{array} \right.\)
Cường độ dòng điện qua R1 là:
\({I_1} = \dfrac{{{U_2}}}{{{R_1}}} = \dfrac{{60}}{{40}} = 1,5{\rm{A}}\)
Công suất tỏa nhiệt trên điện trở R1 là:
\(P = I_1^2{R_1} = 1,{5^2}.40 = 90W\)
Cho mạch điện như hình vẽ. Biết hiệu điện thế giữa hai điểm A và B: UAB = 12 V; điện trở thuần R1 = 6 Ω; biến trở R chỉ có tác dụng tỏa nhiệt. Công suất cực đại của biến trở khi thay đổi giá trị của R là
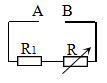
Cường độ dòng điện trong mạch là:
\(I = \dfrac{{{U_{AB}}}}{{{R_1} + R}} = \frac{{12}}{{6 + R}}\)
Công suất của biến trở là:
\(P = {I^2}R = \dfrac{{{{12}^2}}}{{{{\left( {6 + R} \right)}^2}}}.R = \dfrac{{{{12}^2}}}{{{{\left( {\dfrac{6}{R} + 1} \right)}^2}}}\)
P max khi \(\left( {\dfrac{6}{R} + 1} \right)\min \)
\( \Leftrightarrow \dfrac{6}{R} + 1 \ge 2\sqrt {\dfrac{6}{R} + 1} \)
Dấu “=” xảy ra \( \Leftrightarrow \dfrac{6}{R} = 1 \Leftrightarrow R = 6\)
Trong đoạn mạch chỉ có điện trở thuần, với thời gian như nhau, nếu cường độ dòng điện giảm 2 lần thì nhiệt lượng tỏa ra trên mạch
Ta có:
\(\left\{ \begin{array}{l}Q = {I^2}Rt\\Q' = {\left( {\dfrac{I}{2}} \right)^2}Rt\end{array} \right. \Rightarrow \dfrac{Q}{{Q'}} = 4 \Leftrightarrow Q' = \dfrac{Q}{4}\)
=> Nhiệt lượng giảm 4 lần

