Câu hỏi:
2 năm trước
Cho mạch điện có sơ đồ như hình vẽ:
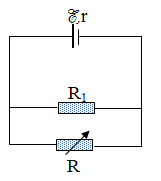
Biết, \(E = 15V,r = 1\Omega ,{R_1} = 2\Omega \), R là biến trở
Tìm R để công suất tiêu thụ trên R là cực đại? Tính giá trị công suất cực đại khi đó?
Trả lời bởi giáo viên
Đáp án đúng: b
Ta có: PR = \(\dfrac{{{U^2}}}{R}\)
Mặt khác: \({U_R} = {\rm{ }}I.{R_N} = \dfrac{E}{{\dfrac{{{R_1}.R}}{{{R_1} + R}} + r}}.\dfrac{{{R_1}.R}}{{{R_1} + R}}\, = \,\dfrac{{30R}}{{3R + 2}}\).
Vậy: \({P_R} = \dfrac{{900{R^2}}}{{{{\left( {3R + 2} \right)}^2}.R}}\, = \,\dfrac{{900}}{{{{\left( {3\sqrt R + \dfrac{2}{{\sqrt R }}} \right)}^2}}}\,\)
Theo BĐT Cô-si, ta có : \(\left( {3\sqrt R + \dfrac{2}{{\sqrt R }}} \right)\, \ge \,2\sqrt 6 \), dấu \('' = ''\) xảy ra khi : \(\left( {3\sqrt R = \dfrac{2}{{\sqrt R }}} \right)\) hay \(R=\dfrac{2}{3}\Omega \).
Vậy : \({P_{RMax}} = \dfrac{{900}}{{{{\left( {2\sqrt 6 } \right)}^2}}}\, = \,37,5{\rm{W}}\)
Hướng dẫn giải:
+ Vận dụng biểu thức tính công suất tiêu thụ trên R : \(P = {I^2}R = \dfrac{{{U^2}}}{R}\)
+ Vận dụng biểu thức tính cường độ dòng điện : \(I = \dfrac{E}{{R + r}}\)
+ Áp dụng bất đẳng thức cosi
Câu hỏi khác
- Bài tập điện năng và công suất điện - định luật jun- lenxơ lý 11 có lời giải
- Bài tập định luật ôm đối với toàn mạch - mắc nguồn điện thành bộ lý 11 có lời giải
- Bài tập tính điện trở dây dẫn - biến trở có lời giải MÔN LÝ lớp 11
- Bài tập định luật ôm cho đoạn mạch chỉ có điện trở lý 11 có lời giải
- Bài tập đại cương về dòng điện không đổi - nguồn điện lý 11 có lời giải.
