Hai đầu tụ điện có điện dung \(20\mu F\) thì hiệu điện thế là \(5V\) thì năng lượng tích được là
Năng lượng điện trường mà tụ điện tích được: \({\rm{W}} = \dfrac{1}{2}C{U^2} = \dfrac{1}{2}{.20.10^{ - 6}}{.5^2} = 2,{5.10^{ - 4}}J = 0,25mJ\)
Một tụ điện được tích điện bằng một hiệu điện thế \(10V\) thì năng lượng của tụ là \(10mJ\). Nếu muốn năng lượng của tụ là \(22,5mJ\) thì phải đặt vào hai đầu tụ một hiệu điện thế:
Ta có:
+ Khi \({U_1} = 10V\) thì \({{\rm{W}}_1} = \dfrac{1}{2}CU_1^2 = 10mJ\) (1)
+ Khi \({U_2} = ?\) thì \({{\rm{W}}_2} = \dfrac{1}{2}CU_2^2 = 22,5mJ\) (2)
Lấy \(\dfrac{{\left( 2 \right)}}{{\left( 1 \right)}}\) ta được:
\(\begin{array}{l}\dfrac{{{{\rm{W}}_2}}}{{{{\rm{W}}_1}}} = \dfrac{{U_2^2}}{{U_1^2}} \Leftrightarrow \dfrac{{22,5}}{{10}} = \dfrac{{U_2^2}}{{{{10}^2}}}\\ \Rightarrow {U_2} = 15V\end{array}\)
Một tụ điện phẳng có điện môi không khí; khoảng cách giữa 2 bản là \(d = 1mm\); diện tích một bản là \(100c{m^2}\). Mắc tụ vào nguồn điện có hiệu điện thế \(U = 220V\). Nếu người ta ngắt tụ điện ra khỏi nguồn rồi nhúng nó chìm hẳn vào một điện môi lỏng có hằng số điện môi \(\varepsilon = 2\). Hiệu điện thế của tụ là:
+ Điện dung của tụ điện:
l\pi }}(nF)\)
+ Điện tích tích trên tụ:
\(Q = C.U = \dfrac{5}{{18\pi }}{.10^{ - 9}}.220 = \dfrac{{55}}{{9\pi }}{.10^{ - 8}}C\)
+ Khi nhúng tụ vào trong dung môi có: \(\varepsilon = 2 \to C' = 2C = 2.\dfrac{5}{{18\pi }}\left( {nF} \right) = \dfrac{5}{{9\pi }}(nF)\)
Khi ngắt tụ ra khỏi nguồn => tụ điện trở thành hệ cô lập => điện tích của tụ không thay đổi:
\( \to Q' = Q \to C'U' = CU \to U' = \dfrac{C}{{C'}}U = \dfrac{U}{2} = \dfrac{{220}}{2} = 110(V)\)
Cho bộ tụ điện mắc như hình vẽ:
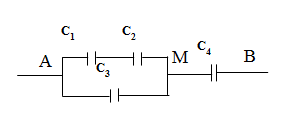
\({C_1} = 4\mu F;{C_2} = {C_4} = 6\mu F;{C_3} = 3,6\mu F\). Mắc 2 cực AB vào hiệu điện thế \(U{\rm{ }} = {\rm{ }}100V\). Điện tích của bộ tụ là:
Cấu tạo của mạch điện: \(\left[ {\left( {{{\rm{C}}_{\rm{1}}}{\rm{ nt }}{{\rm{C}}_{\rm{2}}}} \right){\rm{//}}{{\rm{C}}_{\rm{3}}}} \right]{\rm{ nt }}{{\rm{C}}_{\rm{4}}}\)
Điện dung của bộ tụ:
\(\begin{array}{l}{C_{12}} = \dfrac{{{C_1}{C_2}}}{{{C_1} + {C_2}}} = \dfrac{{6.4}}{{6 + 4}} = 2,4\left( {\mu F} \right)\\{C_{AM}} = {C_{12}} + {C_3} = 2,4 + 3,6 = 6\left( {\mu F} \right)\\{C_{AB}} = \dfrac{{{C_{AM}}{C_4}}}{{{C_{AM}} + {C_4}}} = \dfrac{{6.6}}{{6 + 6}} = 3\left( {\mu F} \right)\end{array}\)
\( \Rightarrow \) Điện tích của bộ tụ: \({Q_{AB}} = {C_{AB}}.U = {3.10^{ - 6}}.100 = {3.10^{ - 4}}C\)
Cho ba tụ mắc như hình vẽ, với \({C_1} = 4\mu F\) có hiệu điện thế giới hạn là \(1000V\), \({C_2} = 2\mu F\) có hiệu điện thế giới hạn \(500V\), \({C_3} = 3\mu F\) có hiệu điện thế giới hạn là \(300V\). Hỏi hai đầu A, B mắc vào nguồn điện có hiệu điện thế tối đa bao nhiêu để bộ tụ không bị hỏng?
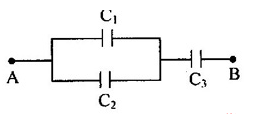
Gọi \(U\) là hiệu điện thế của bộ tụ
+ Từ mạch, ta có: \(\left( {{C_1}//{C_2}} \right)nt{C_3}\)
\({C_{12}} = {C_1} + {C_2} = 4 + 2 = 6\mu F\)
Điện dung của toàn mạch: \(\dfrac{1}{C} = \dfrac{1}{{{C_{12}}}} + \dfrac{1}{{{C_3}}}\)
\( \Rightarrow C = \dfrac{{{C_{12}}{C_3}}}{{{C_{12}} + {C_3}}} = \dfrac{{6.3}}{{6 + 3}} = 2\mu F\)
\( \Rightarrow Q = CU = 2U = {Q_{12}} = {Q_3}\)
+ Điều kiện để bộ tụ tồn tại: \(\left\{ \begin{array}{l}{U_1} = \dfrac{{{Q_{12}}}}{{{C_1}}} = \dfrac{{2U}}{4} \le 1000V\\{U_2} = \dfrac{{{Q_{12}}}}{{{C_2}}} = \dfrac{{2U}}{2} = U \le 500V\\{U_3} = \dfrac{{{Q_3}}}{{{C_3}}} = \dfrac{{2U}}{3} \le 300V\end{array} \right. \Rightarrow \left\{ \begin{array}{l}U \le 2000V\\U \le 500V\\U \le 450V\end{array} \right. \Rightarrow U \le 450V\)
Vậy, cần mắc hai đầu A, B vào nguồn điện có hiệu điện thế tối đa \(450V\) để bộ tụ không bị hỏng.
Tụ xoay có điện dung thay đổi từ \({C_1} = 20pF\) đến \({C_2} = 200pF\) khi góc xoay \(\alpha \) biến thiên từ \({0^0}\) đến \({90^0}\) . Biết điện dung của tụ xoay là hàm bậc nhất của góc xoay \(\alpha \). Biểu thức nào sau đây là đúng?
+ Vì điện dung của tụ là hàm bậc nhất của góc xoay \(\alpha \) nên ta có:
\(C = \alpha a + b\) (a, b là hằng số)
+ Khi \(\alpha = 0\) thì \({C_1} = 20pF\) và khi \(\alpha = {90^0}\) thì \({C_2} = 200pF\) nên, ta có:
\(\left\{ \begin{array}{l}20 = 0{\rm{a}} + b\\200 = 90{\rm{a}} + b\end{array} \right. \to \left\{ \begin{array}{l}a = 2\\b = 20\end{array} \right.\)
=> Biểu thức của điện dung: \(C = 2\alpha + 20{\rm{ }}(pF)\)
Tụ điện phẳng gồm hai bản tụ hình vuông cạnh \(a = 20cm\), đặt cách nhau \(d = 1cm\), chất điện môi giữa hai bản là thủy tinh có \(\varepsilon = 6\). Hiệu điện thế giữa hai bản tụ \(U = 50V\). Điện tích của tụ điện là
+ Diện tích của mỗi bản tụ: \(S = {a^2} = {\left( {{{20.10}^{ - 2}}} \right)^2} = 0,04{m^2}\)
+ Điện dung của tụ điện phẳng: \(C = \dfrac{{\varepsilon S}}{{k.4\pi d}} = \dfrac{{6.\left( {0,04} \right)}}{{{{9.10}^9}.4\pi .\left( {0,01} \right)}} = 2,{12.10^{ - 10}}F\)
+ Điện tích mà tụ điện tích được: \(Q = CU = 2,{12.10^{ - 10}}.50 = 1,{06.10^{ - 8}}C\)
Một tụ điện phẳng không khí, có hai bản hình tròn bán kính \(R = 6cm\) đặt cách nhau một khoảng \(d = 0,5cm\). Đặt vào hai bản một hiệu điện thế \(U = 10V\). Tính điện dung của tụ điện?
Ta có, điện dung của tụ điện phẳng không khí: \(C = \dfrac{S}{{k.4\pi d}}\)
Lại có: diện tích \(S = \pi {R^2}\)
Suy ra: \(C = \dfrac{{\pi {R^2}}}{{k.4\pi d}} = \dfrac{{\pi .{{\left( {0,06} \right)}^2}}}{{{{9.10}^9}.4\pi .\left( {0,{{5.10}^{ - 2}}} \right)}} = {2.10^{ - 11}}F\)
Một tụ điện phẳng có điện dung C = 200pF được tích điện đến hiệu điện thế U = 4 V. Khoảng cách giữa hai bản tụ điện là d = 0,2 mm. Cường độ điện trường trong tụ là:
Cường độ điện trường trong tụ điện là:
\(E = \dfrac{U}{d} = \dfrac{4}{{0,{{2.10}^{ - 3}}}} = 20000V/m\)
Một tụ điện phẳng không khí, có hai bản hình tròn bán kính \(R = 6cm\) đặt cách nhau một khoảng \(d = 0,5cm\). Đặt vào hai bản một hiệu điện thế \(U = 10V\). Tính điện tích của tụ điện?
Ta có, điện dung của tụ điện phẳng không khí: \(C = \dfrac{S}{{k.4\pi d}}\)
Lại có: diện tích \(S = \pi {R^2}\)
Suy ra: \(C = \dfrac{{\pi {R^2}}}{{k.4\pi d}} = \dfrac{{\pi .{{\left( {0,06} \right)}^2}}}{{{{9.10}^9}.4\pi .\left( {0,{{5.10}^{ - 2}}} \right)}} = {2.10^{ - 11}}F\)
+ Điện tích của tụ điện: \(Q = CU = {2.10^{ - 11}}.10 = {2.10^{ - 10}}C\)
Một tụ điện phẳng không khí, có hai bản hình tròn bán kính \(R = 6cm\) đặt cách nhau một khoảng \(d = 0,5cm\). Đặt vào hai bản một hiệu điện thế \(U = 10V\). Tính năng lượng của tụ điện?
Ta có, điện dung của tụ điện phẳng không khí: \(C = \dfrac{S}{{k.4\pi d}}\)
Lại có: diện tích \(S = \pi {R^2}\)
Suy ra: \(C = \dfrac{{\pi {R^2}}}{{k.4\pi d}} = \dfrac{{\pi .{{\left( {0,06} \right)}^2}}}{{{{9.10}^9}.4\pi .\left( {0,{{5.10}^{ - 2}}} \right)}} = {2.10^{ - 11}}F\)
+ Năng lượng của tụ điện: \({\rm{W}} = \dfrac{1}{2}C{U^2} = \dfrac{1}{2}{.2.10^{ - 11}}{.10^2} = {10^{ - 9}}J = 1nJ\)
Một tụ điện phẳng có 2 bản tụ cách nhau \(d = 1,5mm\). Tụ điện tích điện dưới hiệu điện thế \(U = 210V\). Gọi \(\sigma \) là mật độ điện tích trên bản tụ và được đo bằng thương số \(\dfrac{Q}{S}\) ( Q là điện tích, S là diện tích). Tính mật độ điện tích \(\sigma \) trên mỗi bản tụ khi đặt trong dầu hỏa có điện môi \(\varepsilon = 2\)?
Ta có:
+ Mật độ điện tích: \(\sigma = \dfrac{Q}{S}\) (1)
+ \(Q = CU\) (2)
+ Mặt khác: \(C = \dfrac{{\varepsilon S}}{{4\pi k{\rm{d}}}}\) (3)
Từ (1), (2) và (3) ta suy ra:
\(\sigma = \dfrac{Q}{S} = \dfrac{{CU}}{S} = \dfrac{{\dfrac{{\varepsilon S}}{{4\pi k{\rm{d}}}}U}}{S} = \dfrac{{\varepsilon U}}{{4\pi k{\rm{d}}}} = \dfrac{{2.210}}{{4\pi {{.9.10}^9}{\rm{.1,5}}{\rm{.1}}{{\rm{0}}^{ - 3}}}} = 2,{5.10^{ - 6}}(C/{m^2})\)
Tụ phẳng không khí được tích điện bằng nguồn điện có hiệu diện thế không đổi \(U\). Hỏi năng lượng của bộ tụ thay đổi thế nào nếu tăng khoảng cách \(d\) giữa hai bản tụ lên gấp đôi trong trường hợp vẫn nối tụ với nguồn?
Ta có:
+ Điện dung của tụ điện phẳng không khí là: \(C = \dfrac{S}{{k.4\pi d}}\)
+ Khi tăng \(d\) lên gấp đôi thì \(C\) giảm đi một nửa, khi đó \(C' = \dfrac{C}{2}\)
Khi tụ vẫn nối vào nguồn điện thì \(U\) không đổi và năng lượng ban đầu của tụ là \({\rm{W}} = \dfrac{1}{2}C{U^2}\)
Năng lượng của tụ khi tăng \(d\) là \({\rm{W}}' = \dfrac{1}{2}C'{U^2}\)
Vì \(C' = \dfrac{C}{2}\) nên \({\rm{W}}' = \dfrac{{\rm{W}}}{2}\)
Tụ phẳng không khí được tích điện bằng nguồn điện có hiệu diện thế không đổi \(U\). Hỏi năng lượng của bộ tụ thay đổi thế nào nếu tăng khoảng cách \(d\) giữa hai bản tụ lên gấp đôi trong trường hợp ngắt ra khỏi nguồn trước khi tăng?
Ta có:
+ Điện dung của tụ điện phẳng không khí là: \(C = \dfrac{S}{{k.4\pi d}}\)
+ Khi tăng \(d\) lên gấp đôi thì \(C\) giảm đi một nửa, khi đó \(C' = \dfrac{C}{2}\)
Khi ngắt tụ ra khỏi nguồn thì \(Q\) không đổi và năng lượng ban đầu của tụ là \({\rm{W}} = \dfrac{1}{2}\dfrac{{{Q^2}}}{C}\)
Năng lượng của tụ khi tăng \(d\) là \({\rm{W}}' = \dfrac{1}{2}\dfrac{{{Q^2}}}{{C'}}\)
Vì \(C' = \dfrac{C}{2}\) nên \({\rm{W}}' = 2W\)
Một tụ điện phẳng có điện môi không khí; khoảng cách giữa 2 bản là d = 0,5 cm; diện tích một bản là 36 cm2. Mắc tụ vào nguồn điện có hiệu điện thế U =100 V. Tính điện dung của tụ điện và điện tích tích trên tụ.
+ Điện dung của tụ điện:
\(C = \dfrac{{\varepsilon .S}}{{{{9.10}^9}.4\pi .d}} = \dfrac{{{{36.10}^{ - 4}}}}{{{{9.10}^9}.4\pi .0,005}} = \dfrac{1}{{50\pi }}(nF)\)
+ Điện tích tích trên tụ:
\(Q = C.U = \dfrac{1}{{50\pi }}{.10^{ - 9}}.100 = \dfrac{2}{\pi }(nC)\)
Một tụ điện phẳng có điện môi không khí; khoảng cách giữa $2$ bản là $d = 0,5 cm$; diện tích một bản là $36 cm^2$. Mắc tụ vào nguồn điện có hiệu điện thế $U=100 V$. Năng lượng điện trường trong tụ điện là:
+ Điện dung của tụ điện:
\(C = \dfrac{{\varepsilon .S}}{{{{9.10}^9}.4\pi .d}} = \dfrac{{{{36.10}^{ - 4}}}}{{{{9.10}^9}.4\pi .0,005}} = \dfrac{1}{{50\pi }}(nF)\)
+ Năng lượng điện trường:
\(W = \dfrac{1}{2}C{U^2} = \dfrac{1}{2}\dfrac{1}{{50\pi }}{.10^{ - 9}}{.10^4} = \dfrac{{0,1}}{\pi }(\mu J)\)
Một tụ điện phẳng có điện môi không khí; khoảng cách giữa 2 bản là d = 0,5 cm; diện tích một bản là 36 cm2. Mắc tụ vào nguồn điện có hiệu điện thế U=100 V. Nếu người ta ngắt tụ điện ra khỏi nguồn rồi nhúng nó chìm hẳn vào một điện môi lỏng có hằng số điện môi ε = 2. Hiệu điện thế của tụ là:
+ Điện dung của tụ điện:
\(C = \frac{{\varepsilon .S}}{{{{9.10}^9}.4\pi .d}} = \frac{{{{36.10}^{ - 4}}}}{{{{9.10}^9}.4\pi .0,005}} = \frac{1}{{50\pi }}(nF)\)
+ Điện tích tích trên tụ:
\(Q = C.U = \frac{1}{{50\pi }}{.10^{ - 9}}.100 = \frac{2}{\pi }(nC)\)
+ Khi nhúng tụ vào trong dung môi có: \(\varepsilon = 2 \to C' = 2C = \frac{2}{{50\pi }} = \frac{1}{{25\pi }}(F)\)
Khi ngắt tụ ra khỏi nguồn => tụ điện trở thành hệ cô lập => điện tích của tụ không thay đổi:
\( \to Q' = Q \to C'U' = CU \to U' = \frac{C}{{C'}}U = \frac{U}{2} = 50(V)\)
Cho bộ tụ điện mắc như hình vẽ:
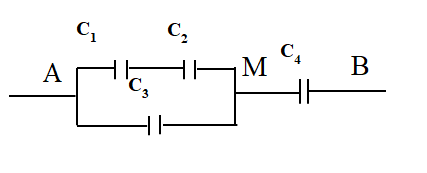
\({C_1} = 4\mu F;{C_2} = {C_4} = 6\mu F;{C_3} = 3,6\mu F\). Mắc 2 cực AB vào hiệu điện thế U = 100V. Điện dung của bộ tụ là:
Cấu tạo của mạch điện: \(\left( {\left( {{{\rm{C}}_{\rm{1}}}{\rm{ nt }}{{\rm{C}}_{\rm{2}}}} \right){\rm{//}}{{\rm{C}}_{\rm{3}}}} \right){\rm{ nt }}{{\rm{C}}_{\rm{4}}}\)
Điện dung của bộ tụ:
\(\begin{array}{l}{C_{12}} = \frac{{{C_1}{C_2}}}{{{C_1} + {C_2}}} = \frac{{6.4}}{{6 + 4}} = 2,4\left( {\mu F} \right)\\{C_{AM}} = {C_{12}} + {C_3} = 2,4 + 3,6 = 6\left( {\mu F} \right)\\{C_{AB}} = \frac{{{C_{AM}}{C_4}}}{{{C_{AM}} + {C_4}}} = \frac{{6.6}}{{6 + 6}} = 3\left( {\mu F} \right)\end{array}\)
Cho bộ tụ điện mắc như hình vẽ.
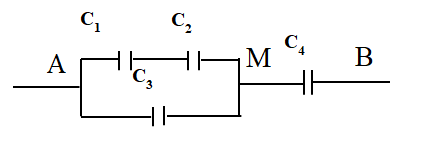
\({C_1} = 4\mu F;{C_2} = {C_4} = 6\mu F;{C_3} = 3,6\mu F\). Nếu hiệu điện thế giới hạn của bộ tụ C1,2,3 (CAM) là 40V; hiệu điện thế giới hạn của tụ C4 là 60V. Thì hiệu điện thế tối đa đặt vào 2 đầu mạch điện là bao nhiêu để các tụ không bị đánh thủng?
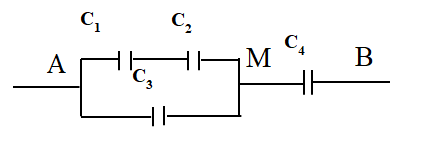
Từ hình vẽ, ta có: Cấu tạo của mạch điện: \(\left[ {\left( {{{\rm{C}}_{\rm{1}}}{\rm{ nt }}{{\rm{C}}_{\rm{2}}}} \right){\rm{//}}{{\rm{C}}_{\rm{3}}}} \right]{\rm{ nt }}{{\rm{C}}_{\rm{4}}}\)
+ Điện dung của bộ tụ:
\(\begin{array}{l}{C_{12}} = \frac{{{C_1}{C_2}}}{{{C_1} + {C_2}}} = \frac{{6.4}}{{6 + 4}} = 2,4\left( {\mu F} \right)\\{C_{AM}} = {C_{12}} + {C_3} = 2,4 + 3,6 = 6\left( {\mu F} \right)\\{C_{AB}} = \frac{{{C_{AM}}{C_4}}}{{{C_{AM}} + {C_4}}} = \frac{{6.6}}{{6 + 6}} = 3\left( {\mu F} \right)\end{array}\)
+ Điện tích của các tụ:
\(\begin{array}{l}{Q_{AB}} = {C_{AB}}.{U_{AB}} = {3.10^{ - 6}}.100 = {3.10^{ - 4}}(C) = {Q_{AM}} = {Q_4}\\{U_{AM}} = \frac{{{Q_{AM}}}}{{{C_{AM}}}} = \frac{{{{3.10}^{ - 4}}}}{{{{6.10}^{ - 6}}}} = 50(V) = {U_{12}} = {U_3}\\{Q_3} = {C_3}.{U_3} = 3,{6.10^{ - 6}}.50 = 1,{8.10^{ - 4}}(C)\\{Q_{12}} = {C_{12}}.{U_{12}} = 2,{4.10^{ - 6}}.50 = 1,{2.10^{ - 4}}(C) = {Q_1} = {Q_2}\end{array}\)
+ Điện tích cực đại có thể tích trên bộ tụ CAM và C4 là:
\(\begin{array}{*{20}{l}}{{Q_{maxAM}} = {\rm{ }}{C_{AM}}.{U_{maxAM}} = {\rm{ }}{{6.10}^{ - 6}}.40{\rm{ }} = {\rm{ }}{{24.10}^{ - 5}}\left( C \right)}\\{{Q_{max4}} = {\rm{ }}{C_4}.{U_{max4}} = {\rm{ }}{{6.10}^{ - 6}}.60{\rm{ }} = {\rm{ }}{{36.10}^{ - 5}}\left( C \right)}\end{array}\)
Mà thực tế ta có vì CAM; C4 mắc nối tiếp nên để không có tụ nào bị đánh thủng thì:
\({Q_{AM}} = {\rm{ }}{Q_4} \le \min \left( {{{\rm{Q}}_{{\rm{maxAM}}}};{{\rm{Q}}_{{\rm{max4}}}}} \right)\)
Điện tích tối đa của bộ:
Hiệu điện thế tối đa có thể đặt vào 2 đầu mạch điện là: \({U_{AB}} = \frac{{{Q_{AB}}}}{{{C_{AB}}}} = \frac{{{{24.10}^{ - 5}}}}{{{{3.10}^{ - 6}}}} = 80(V)\)
Tụ xoay có điện dung thay đổi từ \({C_1} = 30pF\) đến \({C_2} = 120pF\) khi góc xoay biến thiên từ 00 đến 900. Biết điện dung của tụ xoay là hàm bậc nhất của góc xoay . Biểu thức nào sau đây là đúng?
+ Vì điện dung của tụ là hàm bậc nhất của góc xoay nên ta có:
\(C = \alpha a + b\) (a, b là hằng số)
+ Khi \(\alpha = 0\) thì \({C_1} = 30pF\) và khi \(\alpha = {90^0}\) thì \({C_2} = 120pF\) nên, ta có:
\(\left\{ \begin{array}{l}30 = 0{\rm{a}} + b\\120 = 90{\rm{a}} + b\end{array} \right. \to \left\{ \begin{array}{l}a = 1\\b = 30\end{array} \right.\)
=> Biểu thức của điện dung: \(C = \alpha + 30{\rm{ }}(pF)\)

