Một tụ điện phẳng có diện tích \(S = 100c{m^2}\), khoảng cách hai bản là \(d = 1mm\), giữa hai bản là lớp điện môi có \(\varepsilon = 5\). Dùng nguồn \(U = 100V\) để nạp cho tụ điện Điện tích mà tụ điện tích được là:
Ta có:
+ Điện dung của tụ điện: \(C = \frac{{\varepsilon S}}{{{{9.10}^9}.4\pi d}} = \frac{{{{5.100.10}^{ - 4}}}}{{{{9.10}^9}.4\pi {{.10}^{ - 3}}}} = 4,{421.10^{ - 10}}(F)\)
+ Điện tích mà tụ tích được là: \(Q = CU = 4,{421.10^{ - 10}}.100 = 4,{421.10^{ - 8}}(C)\)
Hai bản của một tụ điện phẳng là các hình tròn, tụ điện được tích điện sao cho điện trường trong tụ bằng \({3.10^5}V/m\). Khi đó, điện tích của tụ điện là \(Q = 100nC\), biết bên trong tụ điện là không khí. Bán kính của các bản là:
Ta có:
+ \(C = \frac{{\varepsilon S}}{{4\pi k{\rm{d}}}} = \frac{{\varepsilon \pi {R^2}}}{{4\pi k{\rm{d}}}} = \frac{{\varepsilon {R^2}}}{{4k{\rm{d}}}}\) (1)
+ \(C = \frac{Q}{U} = \frac{Q}{{E{\rm{d}}}}\) (2)
Từ (1) và (2), ta suy ra:
\(\frac{{\varepsilon {R^2}}}{{4k{\rm{d}}}} = \frac{Q}{{E{\rm{d}}}} \to R = \sqrt {\frac{{Q.4k}}{{\varepsilon E}}} = \sqrt {\frac{{{{100.10}^{ - 9}}{{.4.9.10}^9}}}{{{{1.3.10}^5}}}} \approx 0,11m\)
Một tụ điện phẳng có 2 bản tụ cách nhau \(d = 2mm\). Tụ điện tích điện dưới hiệu điện thế \(U = 100V\). Gọi \(\sigma \) là mật độ điện tích trên bản tụ và được đo bằng thương số Q/S ( Q là điện tích, S là diện tích). Tính mật độ điện tích \(\sigma \) trên mỗi bản tụ khi đặt trong dầu hỏa có điện môi \(\varepsilon = 2\)?
Ta có:
+ Mật độ điện tích: \(\sigma = \frac{Q}{S}\) (1)
+ \(Q = CU\) (2)
+ Mặt khác: \(C = \frac{{\varepsilon S}}{{4\pi k{\rm{d}}}}\) (3)
Từ (1), (2) và (3) ta suy ra:
\(\sigma = \frac{Q}{S} = \frac{{CU}}{S} = \frac{{\frac{{\varepsilon S}}{{4\pi k{\rm{d}}}}U}}{S} = \frac{{\varepsilon U}}{{4\pi k{\rm{d}}}} = \frac{{2.100}}{{4\pi {{.9.10}^9}{\rm{.2}}{\rm{.1}}{{\rm{0}}^{ - 3}}}} = 8,{8.10^{ - 7}}(C/{m^2})\)
Một tụ điện phẳng được mắc vào hai cực của một nguồn điện có hiệu điện thế 50V. Ngắt tụ điện ra khỏi nguồn rồi kéo cho khoảng cách giữa hai bản tụ tăng lên gấp đôi so với lúc đầu. Hiệu điện thế của tụ điện khi đó là:
+ Ta có:
\(\begin{array}{l}C = \frac{{\varepsilon S}}{{4\pi k{\rm{d}}}} \to \frac{{{C_2}}}{{{C_1}}} = \frac{{{d_1}}}{{{d_2}}} = \frac{1}{2}\\ \to {C_2} = \frac{{{C_1}}}{2}\end{array}\)
+ Khi ngắt ra khỏi nguồn thì điện tích Q không đổi nên:
\(\begin{array}{l}Q = {C_1}{U_1} = {C_2}{U_2}\\ \to {U_2} = \frac{{{C_1}}}{{{C_2}}}{U_1} = 2{U_1} = 100(V)\end{array}\)
Một tụ điện phẳng không khí, có hai bản hình tròn bán kính
\(R = 6cm\) đặt cách nhau một khoảng \(d = 0,5cm\). Đặt vào hai bản một hiệu điện thế U =10V. Năng lượng của tụ điện là:
+ Ta có, điện dung của tụ điện phẳng không khí:
\(C = \frac{S}{{4\pi k{\rm{d}}}} = \frac{{\pi {R^2}}}{{4\pi k{\rm{d}}}} = \frac{{{{(0,06)}^2}}}{{{{4.9.10}^9}{\rm{.0,5}}{\rm{.1}}{{\rm{0}}^{ - 2}}}} = {2.10^{ - 11}}(F)\)
+ Năng lượng của tụ điện: \({\rm{W}} = \frac{{C{U^2}}}{2} = \frac{{({{2.10}^{ - 11}}){{.10}^2}}}{2} = {10^{ - 9}}(J)\)
Một tụ điện có điện dung \(C = 6\mu F\) được mắc vào nguồn điện hiệu điện thế U = 100V. Sau khi tụ được ngắt ra khỏi nguồn, điện tích của tụ điện phóng qua lớp điện môi trong tụ điện đến khi hết điện tích. Nhiệt lượng tỏa ra ở điện môi trong thời gian phóng điện đó là:
Ta có:
+ Năng lượng của tụ điện: \(W = \frac{1}{2}C{U^2} = \frac{1}{2}({6.10^{ - 6}}){100^2} = 0,03J\)
+ Khi tụ phóng điện qua lớp điện môi thì lớp điện môi nóng lên. Khi hết hẳn điện tích thì toàn bộ năng lượng của tụ chuyển hết thành nhiệt, do đó nhiệt lượng tỏa ra ở điện môi chính bằng năng lượng của tụ điện:
\({Q_{toa}} = {\rm{W}} = 0,03J\)
Năm tụ giống nhau, mỗi tụ có \(C = 0,2\mu F\) mắc nối tiếp. Bộ tụ được tích điện thu năng lượng \(0,2mJ\). Hiệu điện thế trên mỗi tụ là:
Ta có:
+ Điện dung của bộ 5 tụ nối tiếp:
\(\begin{array}{l}\frac{1}{{{C_b}}} = \frac{1}{{{C_1}}} + \frac{1}{{{C_2}}} + \frac{1}{{{C_3}}} + \frac{1}{{{C_4}}} + \frac{1}{{{C_5}}} = \frac{5}{C}\\ \to {C_b} = \frac{C}{5} = \frac{{0,2}}{5} = 0,04\mu F\end{array}\)
+ Năng lượng của bộ tụ: \({\rm{W}} = \frac{1}{2}{C_b}{U^2} \to U = \sqrt {\frac{{2{\rm{W}}}}{{{C_b}}}} = \sqrt {\frac{{2.0,{{2.10}^{ - 3}}}}{{0,{{04.10}^{ - 6}}}}} = 100V\)
Vì 5 tụ mắc nối tiếp, nên:
\(\begin{array}{l}U = {U_1} + {U_2} + {U_3} + {U_4} + {U_5} = 5{U_1}\\ \to {U_1} = \frac{U}{5} = \frac{{100}}{5} = 20V\end{array}\)
Việc hàn mối dây đồng được thực hiện bằng một xung phóng điện của tụ C=1mF được tích điện đến hiệu điện thế U = 1,5kV, thời gian phát xung \(t = 2\mu s\), hiệu suất của thiết bị H = 4%. Công suất trung bình hiệu dụng của mỗi xung là:
+ Năng lượng toàn phần : \({W_0} = \frac{1}{2}C{U^2}\)
=> Năng lượng có ích: \({W_{ich}} = H{{\rm{W}}_0}\)
+ Công suất trung bình mỗi xung: \(P = \frac{{{{\rm{W}}_{ich}}}}{t} = \frac{{H{{\rm{W}}_0}}}{t} = \frac{{HC{U^2}}}{{2t}} = \frac{{0,{{04.10}^{ - 3}}.{{(1,{{5.10}^3})}^2}}}{{{{2.2.10}^{ - 6}}}} = 22,5M{\rm{W}}\)
Cho mạch điện gồm 3 tụ điện \({C_1} = 1\mu F;{C_2} = 1,5\mu F;{C_3} = 3\mu F\) mắc nối tiếp nhau. Đặt vào hai đầu đoạn mạch một hiệu điện thế \({U_{AB}} = 120V\). Điện dung tương đương của bộ tụ là:
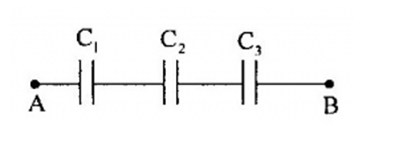
Ta có các tụ mắc nối tiếp,
\(\begin{array}{l}\frac{1}{{{C_b}}} = \frac{1}{{{C_1}}} + \frac{1}{{{C_2}}} + ... + \frac{1}{{{C_n}}}\\ = \frac{1}{1} + \frac{1}{{1,5}} + \frac{1}{3} = 2\\ \to {C_b} = 0,5\mu F\end{array}\)
Cho mạch điện gồm 2 tụ điện \({C_1} = 3\mu F,{C_2} = 2\mu F\) mắc song song. Đặt vào hai đầu đoạn mạch một hiệu điện thế \({U_{AB}} = 25V\). Điện tích của tụ \({Q_1}\) có giá trị là:
Ta có
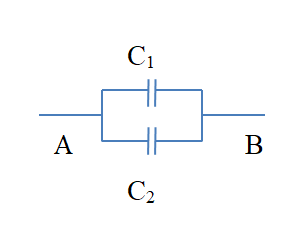
+ Tụ mắc song song nên:
- Điện dung của bộ tụ: \({C_b} = {C_1} + {C_2} = 3 + 2 = 5\mu F\)
- Hiệu điện thế: \({U_1} = {U_2} = {U_{AB}} = 25V\)
+ Điện tích của tụ : \({Q_1} = {C_1}{U_1} = {3.10^{ - 6}}.25 = 75\mu C\)
Cho mạch điện như hình vẽ.
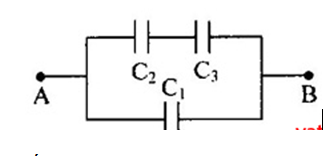
Biết các tụ \({C_1} = 0,25\mu F,{C_2} = 1\mu F,{C_3} = 3\mu F,U = 12V\). Hiệu điện thế trên C3 có giá trị là:
+ Vì tụ và mắc nối tiếp nên: \({\frac{1}{C}_{23}} = \frac{1}{{{C_2}}} + \frac{1}{{{C_3}}} \to {C_{23}} = \frac{{{C_2}{C_3}}}{{{C_2} + {C_3}}} = 0,75\mu F\)
+ Điện dung của bộ tụ: \({C_b} = {C_1} + {C_{23}} = 1\mu F\)
+ Ta có:
\(\begin{array}{l}{U_1} = {U_{23}} = {U_{AB}} = 12V\\ \to \left\{ \begin{array}{l}{Q_1} = {C_1}{U_1} = {3.10^{ - 6}}C\\{Q_{23}} = {C_{23}}{U_{23}} = {9.10^{ - 6}}C\end{array} \right.\end{array}\)
+ Lại có:
\({Q_2} = {Q_3} = {9.10^{ - 6}}C \to {U_3} = \frac{{{Q_3}}}{{{C_3}}} = 3V\)
Cho mạch điện như hình vẽ.
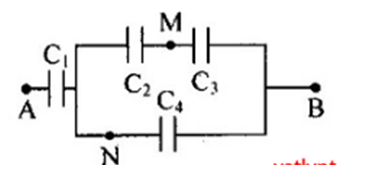
Biết \({C_1} = 6\mu F\), \({C_2} = 3\mu F\), \({C_3} = 6\mu F\), \({C_4} = 1\mu F\), \({U_{AB}} = 60V\).
Hiệu điện thế trên tụ ${C_4}$ có giá trị là:
Từ mạch điện suy ra: \(\left[ {\left( {{C_2}{\rm{ nt }}{C_3}} \right){\rm{//}}{C_4}} \right]{\rm{ nt }}{C_1}\)
Ta có: \({C_{23}} = \frac{{{C_2}{C_3}}}{{{C_2} + {C_3}}} = 2\mu F\)
\(\begin{array}{l} \to {C_{234}} = {C_{23}} + {C_4} = 3\mu F\\ \to {C_b} = \frac{{{C_1}{C_{234}}}}{{{C_1} + {C_{234}}}} = 2\mu F\end{array}\)
Ta có:
\(\begin{array}{l}Q = {Q_1} = {Q_{234}} = 1,{2.10^{ - 4}}C\\ \to \left\{ \begin{array}{l}{U_1} = \frac{{{Q_1}}}{{{C_1}}} = 20V\\{U_{234}} = U - {U_1} = 40V\end{array} \right.\end{array}\)
Mặt khác, ta có: \({U_4} = {U_{24}} = {U_{234}} = 40V\)
Hai tụ không khí phẳng \({C_1} = 0,2\mu F;{C_2} = 0,4\mu F\) mắc song song. Bộ tụ được tích điện đến hiệu điện thế U = 450V rồi ngắt ra khỏi nguồn. Sau đó lấp đầy khoảng giữa hai bản tụ C2 bằng chất điện môi có \(\varepsilon = 2\). Điện tích của tụ 1 có giá trị là:
+ Lúc đầu:
\(\begin{array}{l}{C_b} = {C_1} + {C_2} = 0,2 + 0,4 = 0,6\mu F\\ \to {Q_b} = {C_b}U = 0,{6.10^{ - 6}}.450 = 2,{7.10^{ - 4}}C\end{array}\)
+ Lúc sau:
\(\begin{array}{l}{C_2}' = \varepsilon {C_2} = 2.0,4 = 0,8\mu F\\ \to {C_b}' = {C_1} + {C_2}' = 0,2 + 0,8 = 1\mu F\end{array}\)
+ Vì ngắt tụ ra khỏi nguồn thì $Q$ không đổi nên ta có:
\(U' = \frac{Q}{{{C_b}'}} = \frac{{2,{{7.10}^{ - 4}}}}{{{{10}^{ - 6}}}} = 270V\)
+ Các tụ mắc song song nên: \({U_1}' = {U_2}' = U' = 270V\)
+ Điện tích mới trên tụ : \({Q_1} = {C_1}{U_1}' = 0,{2.10^{ - 6}}.270 = 5,{4.10^{ - 5}}C\)
Có ba tụ \({C_1} = 2\mu F;{C_2} = 4\mu F;{C_3} = 6\mu F\) mắc nối tiếp. Mỗi tụ có hiệu điện thế giới hạn \({U_{gh}} = 3000V\). Tính hiệu điện thế giới hạn của bộ tụ.
Vì các tụ mắc nối tiếp nên:
\(\frac{1}{{{C_b}}} = \frac{1}{{{C_1}}} + \frac{1}{{{C_2}}} + \frac{1}{{{C_3}}} \to {C_b} = \frac{{11}}{{12}}\mu F\)
\({Q_1} = {Q_2} = {Q_3} = {C_b}U = \frac{{12}}{{11}}U(\mu C)\)
Hiệu điện thế trên các tụ là: \(\left\{ \begin{array}{l}{U_1} = \frac{{{Q_1}}}{{{C_1}}} = \frac{{6U}}{{11}}\\{U_2} = \frac{{{Q_2}}}{{{C_2}}} = \frac{{3U}}{{11}}\\{U_3} = \frac{{{Q_3}}}{{{C_3}}} = \frac{{2U}}{{11}}\end{array} \right.\)
Lại có:
\(\begin{array}{l}\left\{ \begin{array}{l}{U_1} \le {U_{gh}}\\{U_2} \le {U_{gh}}\\{U_3} \le {U_{gh}}\end{array} \right. \to \left\{ \begin{array}{l}\frac{{6U}}{{11}} \le 3000\\\frac{{3U}}{{11}} \le 3000\\\frac{{2U}}{{11}} \le 3000\end{array} \right.\\ \to \left\{ \begin{array}{l}U \le 5500V\\U \le 11000V\\U \le 16500V\end{array} \right. \to U \le 5500V\end{array}\)
- Cách giải nhanh:
Vì \(U = \frac{Q}{C}\), mà \({C_1} < {C_2} < {C_3}\) nên \({U_1} > {U_2} > {U_3}\) nên điều kiện để cho bộ tụ tồn tại là hiệu điện thế thành phần lớn nhất cũng phải nhỏ hơn hiệu điện thế giới hạn.
Do đó,
\(\begin{array}{l}{U_1} \le {U_{gh}} \leftrightarrow \frac{{{Q_1}}}{{{C_1}}} \le 3000\\ \leftrightarrow \frac{1}{{{C_1}}}\frac{{12}}{{11}}U \le 3000\\ \to U \le 5500V\end{array}\)
Để tụ tích một điện lượng 10 nC thì đặt vào hai đầu tụ một hiệu điện thế 2V. Để tụ đó tích được điện lượng 2 nC thì phải đặt vào hai đầu tụ một hiệu điện thế
Ta có :
\(Q = C.U \Rightarrow Q \sim C\)
Do đó :
\(U' = \frac{{Q'}}{Q}.U = \frac{2}{{10}}.2 = 0,4V = 400mV\)
Một tụ điện phẳng có các bản đặt nằm ngang và hiệu điện thế giữa hai bản là 300 V. Một hạt bụi nằm lơ lửng trong khoảng giữa hai bản của tụ điện ấy và cách bản dưới một khoảng 0,8 cm. Lấy g = 10 m/s2. Nếu hiệu điện thế giữa hai bản đột ngột giảm bớt đi 60 V thì thời gian hạt bụi sẽ rơi xuống bản dưới gần nhất với giá trị nào sau đây?
Đáp án A
+ Lúc đầu:\(qE = mg \Leftrightarrow q{U \over d} = mg(1)\)
+ Sau khi hiệu điện thế giảm bớt ΔU = 60 V thì:\(mg - q\left( {{{U - \Delta U} \over d}} \right) = ma(2)\)
+ Thay (1) vào (2) ta có:
\(\left( {{{q\Delta U} \over d}} \right) = ma\buildrel {(1)} \over
\longrightarrow {{\Delta U} \over U} = {a \over g} = > a = {{\Delta U} \over U}g = 2(m/{s^2})\)
+ Thời gian rơi của hạt bụi: \(h = {1 \over 2}a{t^2} = > t = \sqrt {{{2h} \over a}} = \sqrt {{{2.0,{{8.10}^{ - 2}}} \over 2}} = 0,09(s)\)=> Chọn A
Đặt vào 2 đầu của một tụ điện một hiệu điện thế U=120V thì điện tích của tụ 24.10-4C. Điện dung của tụ điện:
Ta có: \(C = \dfrac{Q}{U} = \dfrac{{{{24.10}^{ - 4}}}}{{120}} = {2.10^{ - 5}}F = 20\mu F\)
Một tụ điện phẳng có điện dung C = 200pF được tích điện đến hiệu điện thế U = 4 V. Khoảng cách giữa hai bản tụ điện là d = 0,2 mm. Điện tích của tụ điện là:
Điện tích của tụ điện là:
\(Q = CU = {200.10^{ - 12}}.4 = {8.10^{ - 10}}C\)
Hạt bụi khối lượng m = 0,02g mang điện tích q = 5.10-5C đặt sát bản dương của một tụ phẳng không khí. Hai bản tụ có khoảng cách d = 5cm và hiệu điện thế U = 500V. Sau bao lâu hạt bụi chuyển động đến bản tụ âm và vận tốc của nó khi đó. Bỏ qua tác dụng của trọng lực.
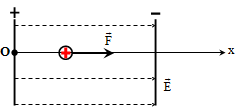
Chọn gốc tọa độ O tại vị trí hạt bụi bắt đầu chuyển động, gốc thời gian là lúc hạt bụi bắt đầu chuyển động. Chiều dương Ox như hình vẽ.
Lực điện trường tác dụng lên hạt bụi là:
\(\overrightarrow F = q\overrightarrow E = m\overrightarrow a \)
Chiếu lên chiều dương Ox ta được:
\(F = qE = ma \Rightarrow a = \dfrac{{qE}}{m} = \dfrac{{qU}}{{m{\rm{d}}}}\)
Phương trình chuyển động của hạt bụi có dạng:
\(x = {x_0} + {v_0}t + \frac{1}{2}a{t^2} \Rightarrow x = \frac{1}{2}a{t^2}\)
\( \Rightarrow x = \dfrac{1}{2}\left( {\dfrac{{qU}}{{m{\rm{d}}}}} \right){t^2} = \dfrac{1}{2}\left( {\dfrac{{{{5.10}^{ - 5}}.500}}{{0,{{02.10}^{ - 3}}.0,05}}} \right){t^2} = 1,{25.10^4}{t^2}\)
Khi hạt bụi đến bản âm, tức là:
\(\begin{array}{l}x = d = {5.10^{ - 2}} \Leftrightarrow 1,{25.10^4}{t^2} = {5.10^{ - 2}}\\ \Rightarrow t = {2.10^{ - 3}}s\end{array}\)
Vận tốc tại bản âm:
\({v^2} - v_0^2 = 2{\rm{a}}.d \Rightarrow v = \sqrt {2{\rm{ad}}} = 50m/s\)
Vậy t = 2.10-3 s và v = 50 m/s.
Tụ điện phẳng không khí có điện dung 5nF. Cường độ điện trường lớn nhất mà tụ có thể chịu được là 3.105 V/m, khoảng cách giữa 2 bản tụ là 2mm. Điện tích lớn nhất có thể tích cho tụ là
Ta có:
\(C = \dfrac{{\varepsilon S}}{{4\pi k{\rm{d}}}} = {5.10^{ - 9}}F\)
\({U_{\max }} = {E_{\max }}.d = {3.10^5}{.2.10^{ - 3}} = 600V\)
Điện tích lớn nhất có thể tích cho tụ là:
\({Q_{\max }} = C.{U_{\max }} = {5.10^{ - 9}}.600 = {3.10^{ - 6}}C\)

