Cho $3$ đường thẳng $a,{\rm{ }}b,{\rm{ }}c$ phân biệt. Trong trường hợp nào thì ba đường thẳng đó đôi một không có giao điểm?
Ba đường thẳng đôi một không có giao điểm nghĩa là:
+ \(a,b\) không có giao điểm hay \(a\) song song \(b\)
+ \(b,c\) không có giao điểm hay \(b\) song song \(c\)
+ \(a,c\) không có giao điểm hay \(a\) song song \(c\)
Vậy ba đường thẳng đôi một song song.
Cho hình vẽ sau
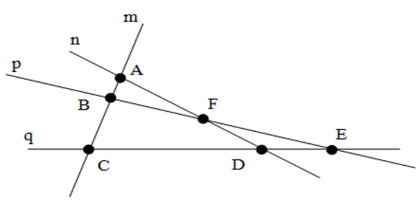
Trên hình vẽ có bao nhiêu đường thẳng đi qua điểm \(B?\)
Điểm \(B\) thuộc các đường thẳng là \(m,p\)
Vậy có \(2\) đường thẳng đi qua \(B\)
Cho hình vẽ sau

Trên hình vẽ, số đường thẳng đi qua điểm \(D\) mà không đi qua điểm \(E\) là:
Điểm \(D\) thuộc các đường thẳng là: \(n,q\)
+ Đường thẳng \(n\) không đi qua \(E\)
+ Đường thẳng \(q\) đi qua \(E\)
Vậy chỉ có \(1\) đường thẳng đí qua \(D\) và không đi qua \(E\)
Cho hình vẽ sau

Trên hình vẽ, điểm \(F\) nằm trên bao nhiêu đường thẳng?
Trên hình vẽ, các đường thẳng đi qua điểm \(F\) là \(n,p\)
Vậy có \(2\) đường thẳng cần tìm.
Cho hình vẽ sau

Trên hình vẽ có bao nhiêu điểm chỉ thuộc hai đường thẳng?
Tất cả các đường thẳng đi qua:
+ Điểm \(A:\) \(m,n\) nên có \(2\) đường thẳng qua \(A\)
+ Điểm \(B:\) \(m,p\) nên có \(2\) đường thẳng qua \(B\)
+ Điểm \(C:\) \(m,q\) nên có \(2\) đường thẳng qua \(C\)
+ Điểm \(D:\) \(n,q\) nên có \(2\) đường thẳng qua \(D\)
+ Điểm \(E:\) \(p,q\) nên có \(2\) đường thẳng qua \(E\)
+ Điểm \(F:\) \(n,p\) nên có \(2\) đường thẳng qua \(F\)
Vậy tất cả \(6\) điểm \(A,B,C,D,E,F\) đều chỉ thuộc hai đường thẳng.
Cho hình vẽ sau

Trên hình vẽ, có bao nhiêu đường thẳng đi qua ba điểm?
Trên hình vẽ, các điểm thuộc đường thẳng:
+ \(m\) là \(A,B,C\) nên có \(3\) điểm thuộc \(m\)
+ \(n\) là \(A,F,D\) nên có \(3\) điểm thuộc \(n\)
+ \(p\) là \(B,F,E\) nên có \(3\) điểm thuộc \(p\)
+ \(q\) là \(C,D,E\) nên có \(3\) điểm thuộc \(q\)
Vậy có tất cả \(4\) đường thẳng mà mỗi đường thẳng đi qua \(3\) điểm trong hình.
Có bao nhiêu bộ ba điểm thẳng hàng trong hình vẽ dưới đây?
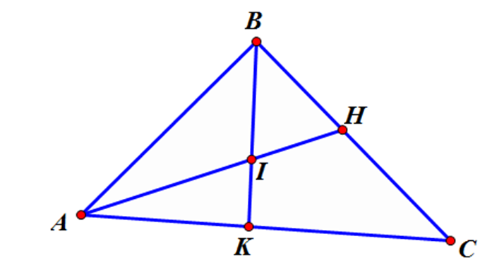
Các bộ ba điểm thẳng hàng trong hình vẽ là:
\(\left( {A,I,H} \right),\left( {B,I,K} \right),\) \(\left( {A,K,C} \right),\left( {B,H,C} \right).\)
Vậy có \(4\) cặp điểm thỏa mãn bài toán.
Cho $100$ điểm trong đó không có $3$ điểm nào thẳng hàng. Hỏi vẽ được bao nhiêu đường thẳng đi qua các cặp điểm.
Gọi các điểm đó có tên lần lượt là \({A_1},...,{A_{100}}\)
+ Qua điểm \({A_1}\) và \(99\) điểm còn lại ta vẽ được \(99\) đường thẳng.
+ Qua điểm \({A_2}\) và \(99\) điểm còn lại ta vẽ được \(99\) đường thẳng.
…
+ Qua điểm \({A_{100}}\) và \(99\) điểm còn lại ta vẽ được \(99\) đường thẳng.
Do đó có \(100.99 = 9900\) đường thẳng.
Tuy nhiên mỗi đường thẳng lại được tính hai lần nên số đường thẳng được tạo thành là: \(9900:2 = 4950\) (đường thẳng)
Có bao nhiêu bộ ba điểm không thẳng hàng trong hình vẽ sau
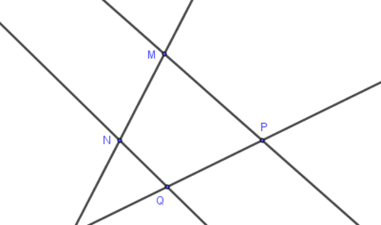
Các bộ ba điểm trong hình vẽ là:
\(\left( {M,N,P} \right),\left( {M,N,Q} \right),\) \(\left( {M,P,Q} \right),\left( {N,P,Q} \right)\)
Vậy có \(4\) bộ ba điểm không thẳng hàng.
Cho trước một số điểm trong đó không có ba điểm nào thẳng hàng. Vẽ đường thẳng đi qua các cặp điểm. Biết tổng số đường thẳng vẽ được là $21.$ Hỏi có bao nhiêu điểm cho trước?
Gọi số điểm cần tìm là \(n\) điểm \(\left( {n \in {N^*}} \right)\)
Ta gọi tên các điểm là \({A_1},{A_2},...,{A_n}\)
+ Qua điểm \({A_1}\) và \(n - 1\) điểm còn lại ta vẽ được \(n - 1\) đường thẳng.
+ Qua điểm \({A_2}\) và \(n - 1\) điểm còn lại ta vẽ được \(n - 1\) đường thẳng.
…
+ Qua điểm \({A_n}\) và \(n - 1\) điểm còn lại ta vẽ được \(n - 1\) đường thẳng.
Do đó có \(n.\left( {n - 1} \right)\) đường thẳng.
Tuy nhiên, mỗi đường thẳng được tính \(2\) lần nên số đường thẳng được tạo thành là: \(n\left( {n - 1} \right):2\) (đường thẳng)
Theo bài ra:
\(n\left( {n - 1} \right):2 = 21\)
\(n\left( {n - 1} \right) = 21.2\)
\(n\left( {n - 1} \right) = 42 = 7.6\)
Vậy \(n = 7\)
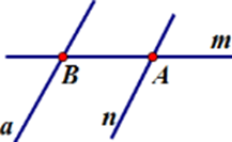
Cho đường thẳng $m$ và đường thẳng $n$ cắt nhau tại $A,$ đường thẳng $a$ không cắt đường thẳng $m$ nhưng cắt đường thẳng $n$ tại $B.$ Hãy chọn hình vẽ đúng trong các hình sau?
Hình A: Có đường thẳng $m$ cắt đường thẳng $n$ tại $A,$ đường thẳng $a$ cắt đường thẳng $m$ tại $B$ nhưng không cắt đường thẳng $n$ (trái với đề bài là $a$ cắt $n$ tại $B$ ) (loại)
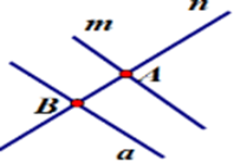
Hình B: Đường thẳng $m$ cắt đường thẳng $n$ tại $A,{\rm{ }}a$ cắt m tại $C,$ cắt $n$ tại $B$ (trái với đề bài là $a$ không cắt $m$) (loại)
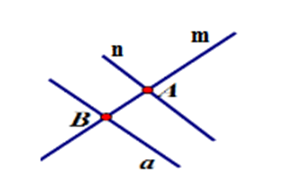
Hình C: Đường thẳng $m$ cắt đường thẳng $n$ tại $A,$ đường thẳng $a$ cắt đường thẳng $n$ tại $B$ và $a$ không cắt $m$ (thỏa mãn)
Hình D: Đường thẳng $a$ cắt đường thẳng $m$ tại $B$ (trái với đề bài là \(a\) không cắt \(m\)) (loại)
Cho hình vẽ sau
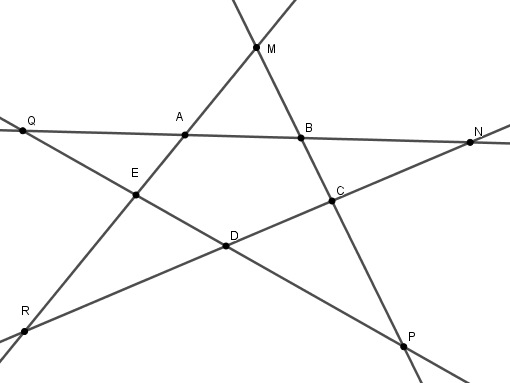
Có bao nhiêu đường thẳng phân biệt trên hình vẽ?
Có \(5\) đường thẳng phân biệt là: \(MR,RN,NQ,QP,PM\)
Cho hình vẽ sau

Có bao nhiêu điểm là giao điểm của đúng hai đường thẳng?
Quan sát hình vé ta thấy các điểm thuộc chỉ \(2\) đường thẳng là:
\(A,B,C,D,E,\) \(M,N,P,Q,R\)
Vậy có \(10\) điểm là giao điểm của hai đường thẳng.
Cho hình vẽ sau

Có bao nhiêu bộ ba đường thẳng đồng qui tại một điểm?
Quan sát hình vẽ ta thấy không có điểm nào mà có cả \(3\) đường thẳng đi qua.
Cho $5$ điểm $A,{\rm{ }}B,{\rm{ }}C,{\rm{ }}D,{\rm{ }}O$ sao cho $3$ điểm $A,{\rm{ }}B,{\rm{ }}C$ cùng thuộc đường thẳng $d;$ $3$ điểm $B,{\rm{ }}C,{\rm{ }}D$ thẳng hàng và $3$ điểm $C,{\rm{ }}D,{\rm{ }}O$ không thẳng hàng. Hỏi điểm nào nằm ngoài đường thẳng $d?$
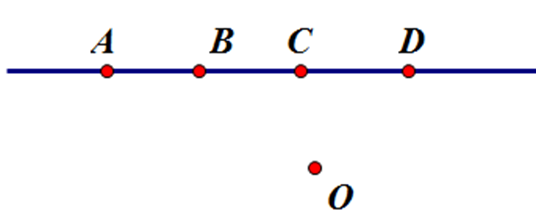
Vì ba điểm \(A,B,C\) thuộc \(d\) và \(B,C,D\) thẳng hàng nên \(D \in d\)
Mà \(C,D \in d\) nên nếu \(C,D,O\) không thẳng hàng thì \(O \notin d\)
Vậy điểm \(O\) không thuộc đường thẳng \(d\)
Cho hình vẽ, biết kéo dài \(a,b\) ta cũng không xác định được điểm chung.
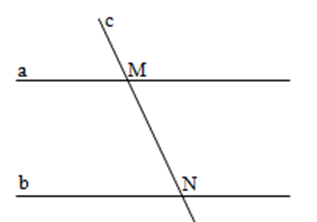
Hai đường thẳng nào song song với nhau?
Từ hình vẽ ta thấy hai đường thẳng \(a,b\) không có điểm chung nên chúng song song.
Hai đường thẳng \(a,c\) có điểm \(M\) chung hay hai đường thẳng \(a,c\) không song song.
Hai đường thẳng \(b,c\) có điểm \(N\) chung hay hai đường thẳng \(b,c\) không song song.
Ngoài ra hai đường thẳng \(MN\) và \(c\) trùng nhau nên chúng cũng không song song.
Cho hình vẽ, biết kéo dài \(a,b\) ta cũng không xác định được điểm chung.

Hãy chỉ ra những cặp đường thẳng cắt nhau và giao điểm của chúng.
Hai đường thẳng \(a,c\) có điểm \(M\) chung.
Hai đường thẳng \(b,c\) có điểm \(N\) chung.
Cho hình vẽ dưới đây
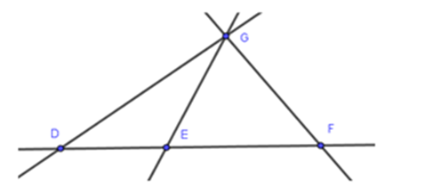
Có tất cả bao nhiêu cách viết tên đường thẳng đi qua $3$ điểm $D,E,F$:
Có $6$ cách viết tên đường thẳng đi qua $3$ điểm $D,{\rm{ }}E,{\rm{ }}F$ là đường thẳng $DE,$ đường thẳng $DF,$ đường thẳng $ED,$ đường thẳng $EF,$ đường thẳng $FE,$ đường thẳng $FD.$
Cho hình vẽ dưới đây

Trong hình có tất cả bao nhiêu đường thẳng phân biệt?
Trong hình có 4 đường thẳng phân biệt, đó là đưởng thẳng $DE,$ đưởng thẳng $GD,$ đưởng thẳng $GE,$ đưởng thẳng $GF.$