Kết quả:
0/25
Thời gian làm bài: 00:00:00
Với giá trị nào của \(m\) dưới đây thì phương trình \(\sin x = m\) có nghiệm?
Số nghiệm của phương trình \(\tan x = \tan \dfrac{{3\pi }}{{11}}\) trên khoảng \(\left( {\dfrac{\pi }{4};2\pi } \right)\) là:
Giải phương trình \(\sin 18x\cos 13x = \sin 9x\cos 4x\).
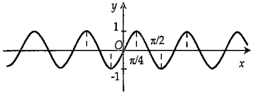
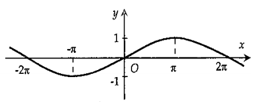
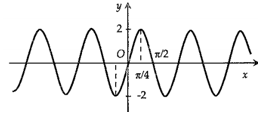
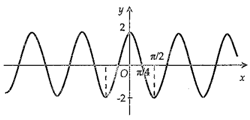
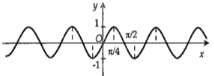
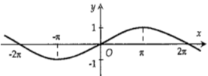
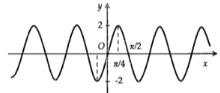
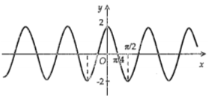
Hình nào dưới đây biểu diễn đồ thị hàm số \(y = f(x) = 2\sin 2x?\)
Trong mặt phẳng tọa độ \(Oxy\) cho đường thẳng \(\Delta :\,x + 2y - 1 = 0\) và điểm \(I\left( {1;0} \right)\). Phép vị tự tâm \(I\) tỉ số \(k\) biến đường thẳng \(\Delta \) thành \(\Delta '\) có phương trình là:
Điền cụm từ thích hợp vào chỗ chấm: “Phép đồng nhất là phép biến hình biến điểm \(M\) thành …”.
Hình nào sau đây có trục đối xứng và đồng thời có tâm đối xứng?
Trong mặt phẳng tọa độ $Oxy$ cho phép quay tâm $O$ biến điểm \(A\left( {1;0} \right)\) thành điểm \(A'\left( {0;1} \right)\). Khi đó nó biến điểm \(M\left( {1; - 1} \right)\) thành điểm:
Cho hình bình hành ABCD. Phép tịnh tiến theo \({T_{\overrightarrow {AB} - \overrightarrow {AC} }}\) biến đoạn thẳng DC thành đoạn thẳng nào sau đây?
Tìm m để phương trình $m\sin x + 5\cos x = m + 1$ có nghiệm.
Trong mặt phẳng với hệ tọa độ $Oxy$ , cho $T$ là một phép tịnh tiến theo vectơ $\overrightarrow u $ biến điểm $M\left( {x;y} \right)$ thành điểm $M'\left( {x';y'} \right)$ với biểu thức tọa độ là: $x = x' + 3;\,\,y = y' - 5$. Tọa độ của vectơ tịnh tiến $\overrightarrow u $ là:
Số phát biểu đúng trong các phát biểu sau:
(1) Phép tịnh tiến và phép đối xứng trục đều biến đường thẳng thành đường thẳng song song, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đương tròn thành đường tròn có cùng bán kính.
(2) Tứ giác $ABCD$ là hình thang cân đáy \(AD//BC\). Gọi $M,N$ lần lượt là trung điểm của hai cạnh bên $AB$ và $CD$. Khi đó, đường thẳng $MN$ là trục đối xứng của $ABCD$.
(3) Cho đường thẳng $d$ có phương trình \(y = - x\). Ảnh của đường tròn \(\left( C \right):\,\,{\left( {x - 5} \right)^2} + {\left( {y - 3} \right)^2} = 7\) qua phép đối xứng trục $d$ là \(\left( {C'} \right):\,\,{\left( {x - 5} \right)^2} + {\left( {y + 3} \right)^2} = 7\)
(4) Ảnh của đường phân giác ứng với góc phần tư thứ $(I)$ qua phép đối xứng trục $Oy$ là đường thẳng $d$ có phương trình \(y = - x\)
Hình nào dưới đây biểu diễn đồ thị hàm số \(y = f\left( x \right) = 2\sin 2x\).
Giải phương trình \(\cot \left( {3x - 1} \right) = - \sqrt 3 .\)
Mệnh đề nào sau đây là đúng?
Điểm \(O\left( {0;0} \right)\) luôn thuộc đồ thị hàm số
Tìm giá trị nhỏ nhất, giá trị lớn nhất của hàm số \(y = 3\sin x + 4\cos x - 1\):
Phương trình \(\cos 11x\cos 3x = \cos 17x\cos 9x\) có nghiệm là:
Giải phương trình \(2{\sin ^2}2x + \sin 7x - 1 = \sin x\).
Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(y = \dfrac{{{\mathop{\rm s}\nolimits} {\rm{inx}} + 2\cos x + 3}}{{2 + \cos x}}\)
Trong mặt phẳng tọa độ $Oxy$ cho đường thẳng \(\Delta \) có phương trình \(y = - 3x + 2\). Thực hiện liên tiếp hai phép tịnh tiến theo các vectơ \(\vec u = \left( { - 1;2} \right)\) và \(\vec v = \left( {3;1} \right)\) thì đường thẳng \(\Delta \) biến thành đường thẳng \(d\) có phương trình là:
Trong mặt phẳng \(Oxy,\) cho hai đường tròn \(\left( {{C_1}} \right):{\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} = 1;\,\)\(\left( {{C_2}} \right):{\left( {x - 4} \right)^2} + {\left( {y - 3} \right)^2} = 4.\) Tìm tâm vị tự ngoài của hai đường tròn.
Số các giá trị nguyên của \(m\) để phương trình \({\cos ^2}x + \sqrt {\cos x + m} = m\) có nghiệm là:
Phương trình \(\tan \left( {\dfrac{\pi }{2} - x} \right) + 2\tan \left( {2x + \dfrac{\pi }{2}} \right) = 1\) có nghiệm là:
Trong mặt phẳng \(Oxy\), tìm phương trình đường tròn \(\left( {C'} \right)\) là ảnh của đường tròn \(\left( C \right)\): \({x^2} + {y^2} = 1\) qua phép đối xứng tâm \(I\left( {1;\;0} \right)\).