Kết quả:
0/25
Thời gian làm bài: 00:00:00
Giá trị \(\lim \left( {{n^3} - 2n + 1} \right)\) bằng
Cho hàm số \(f\left( x \right) =\) \( \left\{ \begin{array}{l}\dfrac{{\tan x}}{x}\,\,\,khi\,\,x \ne 0,x \ne \dfrac{\pi }{2} + k\pi \,\,\left( {k \in Z} \right)\\0\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x = 0\end{array} \right.\). Hàm số \(y = f\left( x \right)\) liên tục trên các khoảng nào sau đây?
Tính $\mathop {\lim }\limits_{x \to 2} \dfrac{{x - \sqrt {x + 2} }}{{\sqrt {4x + 1} - 3}}$ bằng?
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{3 - \sqrt {9 - x} }}{x}\,\,\,khi\,\,0 < x < 9\\m\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x = 0\\\dfrac{3}{x}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x \ge 9\end{array} \right.\). Tìm \(m\) để \(f\left( x \right)\) liên tục trên \(\left[ {0; + \infty } \right)\).
Hàm số \(y = f\left( x \right)\) có đồ thị dưới đây gián đoạn tại điểm có hoành độ bằng bao nhiêu?
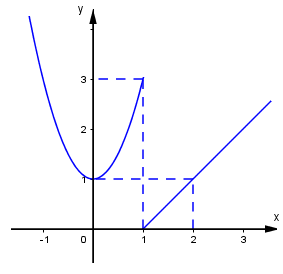
Giới hạn $\lim \left( {\sqrt {{n^2} - n + 1} - \sqrt {{n^2} + 1} } \right)$ bằng?
Tính $\mathop {\lim }\limits_{x \to - 1} \left( {{x^2} - x + 7} \right)$ bằng?
Tính $\mathop {\lim }\limits_{x \to 0} \dfrac{{1 - \sqrt[3]{{x + 1}}}}{{3x}}$ bằng?
Hàm số \(f\left( x \right) = \left\{ \begin{array}{l} - x\cos x\,\,\,khi\,\,x < 0\\\dfrac{{{x^2}}}{{1 + x}}\,\,\,\,\,\,\,\,\,\,khi\,\,0 \le x < 1\\{x^3}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x \ge 1\end{array} \right.\)
Tính $\mathop {\lim }\limits_{x \to - 2} \left( {3{x^2} - 3x - 8} \right)$ bằng?
Chọn mệnh đề sai:
Cho $n\in N^*$, nếu \(\left| q \right| < 1\) thì:
Dãy số nào dưới đây không có giới hạn \(0\)?
Trong các giới hạn sau giới hạn nào bằng $-1$?
Giới hạn $\lim \dfrac{{\sqrt {{n^2} - 3n - 5} - \sqrt {9{n^2} + 3} }}{{2n - 1}}$bằng?
Cho dãy số $({u_n})$ với ${u_n} = \dfrac{{\left( {2n + 1} \right)\left( {1 - 3n} \right)}}{{\sqrt[3]{{{n^3} + 5n - 1}}}}$. Khi đó $\lim {u_n}$ bằng?
Tính $\mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {{x^2} + 1} + x - 1} \right)$ bằng?
Tính$\mathop {\lim }\limits_{x \to - \infty } (x - 1)\sqrt {\dfrac{{{x^2}}}{{2{x^4} + {x^2} + 1}}} $ bằng?
Tính $\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} + x + 3} - x} \right)$ bằng?
Cho $a$ và $b$ là các số thực khác $0.$ Tìm hệ thức liên hệ giữa $a$ và $b$ để hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{\sqrt {ax + 1} - 1}}{x}\,\,\,khi\,\,x \ne 0\\4{x^2} + 5b\,\,\,\,\,\,\,\,\,khi\,\,x = 0\end{array} \right.\) liên tục tại $x = 0.$
Cho hàm số \(f\left( x \right)\) xác định trên $[a; b].$ Trong các khẳng định sau, khẳng định nào đúng?
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\sqrt {2x - 4} + 3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x \ge 2\\\dfrac{{x + 1}}{{{x^2} - 2mx + 3m + 2}}\,\,khi\,\,x < 2\end{array} \right.\)
Tìm tất cả các giá trị của tham số $m$ để hàm số liên tục trên $R.$
Cho dãy số $({u_n})$xác định bởi $\left\{ \begin{array}{ccccc}u _{1} = 1\\{u_{n + 1}} = \sqrt {{u_n}\left( {{u_n} + 1} \right)\left( {{u_n} + 2} \right)\left( {{u_n} + 3} \right) + 1} ,\,\,\left( {n \ge 1} \right)\end{array} \right.\,\,$. Đặt ${v_n} = \sum\limits_{i = 1}^n {\dfrac{1}{{{u_i} + 2}}} $. Tính $\lim {v_n}$bằng?
Tính $\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt[n]{{(x + 1)(x + 2)...(x + n)}} - x} \right)$ bằng:
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{\sqrt {x + 6} - a}}{{\sqrt {x + 1} - 2}}\,\,\,\,\,\,\,\,\,\,\,khi\,\,x \ne 3\\{x^3} - \left( {2b + 1} \right)x\,\,\,\,khi\,\,x = 3\end{array} \right.\) trong đó $a, b$ là các tham số thực. Biết hàm số liên tục tại $x = 3$. Số nhỏ hơn trong hai số $a$ và $b$ là:

