Đề kiểm tra học kì 1 - Đề số 3

Trong mặt phẳng tọa độ \(Oxy\) cho phép quay tâm \(O\) biến điểm \(A\left( {1;0} \right)\) thành điểm \(A'\left( {0;1} \right).\) Khi đó nó biến điểm \(M\left( {1; - 1} \right)\) thành điểm:

Cho đường thẳng \(d\) và mặt phẳng \(\left( \alpha  \right)\) như hình vẽ, số điểm chung của \(d\) và \(\left( \alpha  \right)\) là:

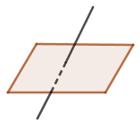
Trong các mệnh đề sau, mệnh đề nào đúng?

Một hộp đựng $11$ thẻ được đánh số \(1,2,3, \ldots ,11\). Rút ngẫu nhiên $3$ thẻ và tính tổng các số ghi trên ba thẻ đó. Tính xác suất để tổng nhận được bằng $12$.

Trong mặt phẳng tọa độ $Oxy$, phép đối xứng trục biến điểm $A\left( {2;1} \right)$ thành $A'\left( {2;5} \right)$ có trục đối xứng là:

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Một mặt phẳng (P) đồng thời song song với AC và SB lần lượt cắt các đoạn thẳng SA, AB, BC, SC, SD và BD tại M, N, E, F, I, J. Xét các khẳng định sau:

(1) MN // (SCD)                            (2) EF // (SAD)

(3) NE // (SAC)                             (3) IJ // (SAB)

Có bao nhiêu khẳng định đúng?

Cho hình vẽ sau :

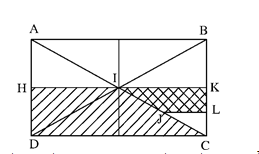
Xét phép đồng dạng biến hình thang $HICD$ thành hình thang $LJIK$. Tìm khẳng định đúng :

Hàm số nào sau đây có đồ thị không là đường hình sin?

Với giá trị nào của \(m\) dưới đây thì phương trình \(\sin x = m\) có nghiệm?

Công việc \(A\) có \(k\) phương án \({A_1},...,{A_k}\) để thực hiện. Biết có \({n_1}\) cách thực hiện \({A_1}\),…,\({n_k}\) cách thực hiện \({A_k}\). Số cách thực hiện công việc \(A\) là:

Phương trình \(\sqrt 3 \sin 2x - \cos 2x + 1 = 0\) có nghiệm là:

Cho hai đường thẳng \(d\) và \(d'\) song song với nhau. Có bao nhiêu phép tịnh tiến biến \(d\) thành \(d'\)?

Khẳng định nào sau đây đúng về phép quay :

Số phần tử của tập hợp các điểm chung của một đường thẳng và một mặt phẳng không thể là:

Trong các mệnh đề sau, mệnh đề nào đúng?

Điểm \(O\left( {0;0} \right)\) luôn thuộc đồ thị hàm số

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P theo thứ tự là trung điểm của SA, SD và AB. Khẳng định nào sau đây đúng?

Tìm mệnh đề đúng trong các mệnh đề sau:

Một tổ có 7 nam và 3 nữ. Chọn ngẫu nhiên 2 người. Tính xác suất sao cho 2 người được chọn có đúng một người nữ.

Cho cấp số cộng \({u_1};\,{\rm{ }}{u_2};{\rm{ }}{u_3};{\rm{ }} \cdots ;{\rm{ }}{u_n}\) có công sai \(d,\) các số hạng của cấp số cộng đã cho đều khác \(0.\) Với giá trị nào của \(d\) thì dãy số \(\dfrac{1}{{{u_1}}};\,{\rm{ }}\dfrac{1}{{{u_2}}};{\rm{ }}\dfrac{1}{{{u_3}}};{\rm{ }} \cdots ;{\rm{ }}\dfrac{1}{{{u_n}}}\) là một cấp số cộng?

Giá trị của biểu thức \(S = {9^{99}}C_{99}^0 + {9^{98}}C_{99}^1 + {9^{97}}C_{99}^2 + ... + 9C_{99}^{98} + C_{99}^{99}\)\(\) bằng:

Cho một đường thẳng \(a\) song song với mặt phẳng \(\left( P \right)\). Có bao nhiêu mặt phẳng chứa \(a\) và song song với \(\left( P \right)\)?

Bạn muốn mua một cây bút mực và một cây bút chì. Các cây bút mực có $8$ màu khác nhau, các cây bút chì cũng có $8$ màu khác nhau. Như vậy bạn có bao nhiêu cách chọn

Tìm số hạng lớn nhất của dãy số \(\left( {{a_n}} \right)\) có \({a_n} =  - {n^2} + 4n + 11,\,\,\forall n \in N^*\) .

Cho \(\Delta ABC\) và \(\Delta A'B'C'\) đồng dạng với nhau theo tỉ số \(k\). Chọn câu sai:

Cho các mệnh đề sau:

1. Qua một điểm không thuộc hai mặt phẳng cắt nhau vẽ được duy nhất một đường thẳng song song với hai mặt đó.

2. Ba đường thẳng đôi một cắt nhau thì xác định một mặt phẳng.

3. Qua một điểm không thuộc hai đường thẳng chéo nhau vẽ được duy nhất một mặt phẳng song song với hai đường thẳng đó.

4. Ba mặt phẳng phân biệt cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến đó hoặc đồng quy hoặc song song.

5. Nếu đường thẳng $d$ song song với đường thẳng $d’$ trong mặt phẳng $(P)$ thì đường thẳng $d$ song song hoặc nằm trong mặt phẳng $(P).$

6. Hai mặt phẳng cùng song song với một đường thẳng thì cắt nhau theo giao tuyến song song với đường thẳng đó.

Hãy chọn các mệnh đề đúng:

Cho 3 đường thẳng \({d_1},\;{d_2},\;{d_3}\) không cùng thuộc một mặt phẳng và cắt nhau từng đôi. Khẳng định nào sau đây đúng?

Cho năm điểm \(A,B,C,D,E\) trong đó không có bốn điểm nào ở trên cùng một mặt phẳng. Hỏi có bao nhiêu mặt phẳng tạo bởi ba trong số năm điểm đã cho?

Số tổ hợp chập \(6\) của \(7\) phần tử là:

Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y = 3\sin x + 4\cos x + 1\):

Tập nghiệm của phương trình \(\tan x.\cot x = 1\) là:

Để phương trình \(\dfrac{{{a^2}}}{{1 - {{\tan }^2}x}} = \dfrac{{{{\sin }^2}x + {a^2} - 2}}{{\cos 2x}}\) có nghiệm, tham số a phải thỏa mãn điều kiện:

Có bao nhiêu cách sắp xếp $3$ nữ sinh, $3$ nam sinh thành một hàng dọc sao cho các bạn nam và nữ ngồi xen kẻ:

Có bao nhiêu số có \(5\) chữ số đôi một khác nhau tạo thành từ các chữ số \(1,2,3,4,5\)?

Cho khai triển ${\left( {\sqrt {{x^3}}  + \dfrac{3}{{\sqrt[3]{{{x^2}}}}}} \right)^n}$ với $x > 0.$ Biết tổng hệ số của ba số hạng đầu tiên của khai triển là $631.$ Tìm hệ số của số hạng chứa ${x^5}.$

Chọn ngẫu nhiên 6 số nguyên dương trong tập ${\rm{\{ 1;2;}}...{\rm{;10\} }}$và sắp xếp chúng theo thứ tự tăng dần. Gọi $P$ là xác suất để số 3 được chọn và xếp ở vị trí thứ 2. Khi đó $P$ bằng

Một gia đình cần khoan một cái giếng để lấy nước. Họ thuê một đội khoan giếng nước đến để khoan giếng nước. Biết giá của mét khoan đầu tiên là 80.000 đồng, kể từ mét khoan thứ 2 giá của mỗi mét khoan tăng thêm 5000 đồng so với giá của mét khoan trước đó. Biết cần phải khoan sâu xuống 50m mới có nước. Vậy hỏi phải trả bao nhiêu tiền để khoan cái giếng đó?

Trong mặt phẳng tọa độ $Oxy$ cho hai đường thẳng song song $a$ và $a'$  lần lượt có phương trình \(3x - 4y + 5 = 0\) và \(3x - 4y = 0\). Phép tịnh tiến theo \(\overrightarrow u \) biến đường thẳng $a$ thành đường thẳng $a'$. Khi đó độ dài bé nhất của vectơ \(\overrightarrow u \) bằng bao nhiêu?

Cho hình thoi \(ABCD\) có góc \(\widehat {ABC} = {60^0}\) (các đỉnh của hình thoi ghi theo chiều kim đồng hồ). Ảnh của cạnh \(CD\) qua phép quay \({Q_{\left( {A,{{60}^0}} \right)}}\) là:

Trong mặt phẳng \(Oxy,\) cho điểm \(M\left( {2;4} \right)\). Hỏi phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm \(O\) tỉ số \(k = \dfrac{1}{2}\) và phép quay tâm \(O\) góc quay \( - {90^0}\) sẽ biến điểm \(M\) thành điểm nào sau đây?

Cho tứ diện \(ABCD\), gọi \(M,N\) lần lượt là hai điểm thuộc các đoạn thẳng \(AB,AC\). Giao tuyến của hai mặt phẳng \(\left( {DBN} \right)\) và \(\left( {DCM} \right)\) là

Cho tứ diện $ABCD.$ Gọi $M,N,P,Q$ lần lượt là trung điểm $AC, BC, BD, AD.$ Tìm điều kiện của tứ diện $ABCD$ để $MNPQ$ là hình thoi?

Cho tứ diện \(ABCD\,.\) Gọi \(M,\,\,N\) lần lượt là trung điểm các cạnh \(AB\) và \(AC,\) \(E\) là điểm trên cạnh \(CD\) với \(ED = 3EC.\) Thiết diện tạo bởi mặt phẳng \(\left( {MNE} \right)\) và tứ diện \(ABCD\) là:

Cho đường thẳng $a$ song song với mặt phẳng $(P).$ Khi đó, số đường thẳng phân biệt nằm trong $(P)$ và song song với $a $ có thể là:

Cho hình chóp $S.ABCD$ có đáy $ABCD$  là hình thang có đáy lớn $BC$ , đáy nhỏ $AD$.  Mặt bên $\left( {SAD} \right)$  là tam giác đều, \(\left( \alpha  \right)\) là mặt phẳng đi qua $M$  trên cạnh $AB$ , song song với $SA,BC$ . Mp\(\left( \alpha  \right)\)cắt các cạnh $CD,SC,SB$  lần lượt tại $N,P,Q.MNPQ$  là hình gì?

Cho đường tròn $\left( {O;R} \right)$ và hai điểm $A,B$ phân biệt. Một điểm $M$ thay đổi trên đường tròn $\left( O \right)$. Khi đó tập hợp các điểm $N$ sao cho $\overrightarrow {MN}  + \overrightarrow {MA}  = \overrightarrow {MB} $ là tập nào sau đây?

Cho tứ diện $ABCD,$ $M$ là trung điểm của cạnh $CD,$ $G$ là trọng tâm tứ diện. Khi đó 2 đường thẳng $AD$ và $GM $ là hai đường thẳng:

Một lớp học có $n$ học sinh $\left( {n > 3} \right)$. Thầy chủ nhiệm cần chọn ra một nhóm và cần cử ra $1$  học sinh trong nhóm đó làm nhóm trưởng. Số học sinh trong mỗi nhóm phải lớn hơn $1$ và nhỏ hơn $n$. Gọi $T$ là số cách chọn. Lúc này:

Phương trình $\tan x + \tan \left( {x + \dfrac{\pi }{3}} \right) + \tan \left( {x + \dfrac{{2\pi }}{3}} \right) = 3\sqrt 3 $ tương đương với phương trình.

Cho dãy số \(\left( {{u_n}} \right)\) thỏa mãn \({u_1} = \dfrac{1}{2};{u_{n + 1}} = \dfrac{{{u_n}}}{{2\left( {n + 1} \right){u_n} + 1}},\,\,n \ge 1\) . \({S_n} = {u_1} + {u_2} + ... + {u_n} < \dfrac{{2017}}{{2018}}\) khi $n$ có giá trị dương lớn nhất là: