Cho tứ diện \(ABCD\), gọi \(M,N\) lần lượt là hai điểm thuộc các đoạn thẳng \(AB,AC\). Giao tuyến của hai mặt phẳng \(\left( {DBN} \right)\) và \(\left( {DCM} \right)\) là
Trả lời bởi giáo viên
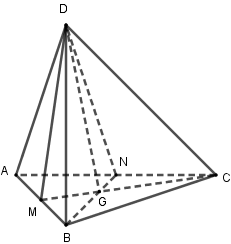
Dễ thấy \(D\) là điểm chung thứ nhất của hai mặt phẳng.
Trong mp\(\left( {ABC} \right)\) gọi \(G = BN \cap CM\) \( \Rightarrow \left\{ \begin{array}{l}G \in BN \subset \left( {BDN} \right)\\G \in CM \subset \left( {DCM} \right)\end{array} \right.\) \( \Rightarrow G \in \left( {DBN} \right) \cap \left( {DCM} \right)\)
\( \Rightarrow DG = \left( {DBN} \right) \cap \left( {DCM} \right)\).
Do \(M,N\) là các điểm bát kì thuộc hai đoạn thẳng \(AB,AC\) nên ta chưa thể kết luận được vị trí của \(G\).
Hướng dẫn giải:
- Dựng hình, xác định điểm chung thứ nhất của hai mặt phẳng.
- Tìm điểm chung thứ hai (tìm hai đường thẳng lần lượt thuộc hai mặt phẳng mà cắt nhau).