Kết quả:
0/25
Thời gian làm bài: 00:00:00
Cho cấp số nhân$\left( {{u_n}} \right)$có ${u_1} = - 1;\,q = \dfrac{{ - 1}}{{10}}$. Số $\dfrac{1}{{{{10}^{103}}}}$ là số hạng thứ bao nhiêu?
Cho cấp số nhân $\left( {{u_n}} \right)$, biết: ${u_1} = - 2,{u_2} = 8$ . Lựa chọn đáp án đúng.
Tìm số hạng đầu và công bội của cấp số nhân \(\left( {{u_n}} \right)\) có công bội \(q > 0\) . Biết \({u_2} = 4;{u_4} = 9\) .
Trong các dãy số dưới đây, dãy số nào là dãy số tăng?
Dãy số nào trong các dãy số sau không phải là cấp số nhân:
Trong các dãy số sau, dãy số nào không là cấp số cộng?
Trong các dãy số sau, dãy số nào là cấp số cộng?
Số đo bốn góc của một tứ giác lồi lập thành một cấp số nhân, biết rằng số đo của góc lớn nhất gấp $8$ lần số đo của góc nhỏ nhất. Tìm góc lớn nhất:
Cho cấp số nhân $\left( {{u_n}} \right)$, biết: ${u_1} = 3,{u_5} = 48$ . Lựa chọn đáp án đúng.
Cho hai dãy số \(\left( {{x_n}} \right)\) với \({x_n} = \dfrac{{\left( {n + 1} \right)!}}{{{2^n}}}\) và \(\left( {{y_n}} \right)\) với \({y_n} = n + {\sin ^2}\left( {n + 1} \right)\) . Mệnh đề nào dưới đây là đúng?
Cho dãy số $\left( {{u_n}} \right)$, biết ${u_n} = \dfrac{{ - n}}{{n + 1}}.$ Năm số hạng đầu tiên của dãy số đó lần lượt là những số nào dưới đây?
Cho các số thực $x,y,z$ thỏa mãn điều kiện ba số \(\dfrac{1}{{x + y}},\dfrac{1}{{y + z}},\dfrac{1}{{z + x}}\) theo thứ tự lập thành một cấp số cộng. Mệnh đề nào dưới đây là mệnh đề đúng ?
Nghiệm của phương trình $1 + 7 + 13 + \ldots + x = 280$ là:
Cho dãy số $\left( {{u_n}} \right)$, biết $\left\{ \begin{array}{l}{u_1} = - 1\\{u_{n + 1}} = {u_n} + 3\end{array} \right.$với \(n \ge 1\). Ba số hạng đầu tiên của dãy số đó là lần lượt là những số nào dưới đây?
Cho dãy số \(\left( {{a_n}} \right)\) xác định bởi \({a_1} = 1\) và \({a_{n + 1}} = - \dfrac{3}{2}a_n^2 + \dfrac{5}{2}{a_n} + 1,\,\,\forall n \in N^*.\) Mệnh đề nào dưới đây là đúng ?
Biết rằng tồn tại các giá trị của \(x \in \left[ {0;2\pi } \right]\) để ba số \(1 + \sin x,\,\,{\sin ^2}x,\,\,1 + \sin 3x\) lập thành một cấp số cộng, tính tổng $S$ các giá trị đó của $x$.
Độ dài $3$ cạnh của một tam giác vuông lập thành một cấp số cộng . Nếu trung bình cộng ba cạnh bằng $6$ thì công sai của cấp số cộng này là:
Cho ba số dương $a,b,c$ thỏa mãn điều kiện \(\dfrac{1}{{\sqrt b + \sqrt c }},\dfrac{1}{{\sqrt c + \sqrt a }},\dfrac{1}{{\sqrt a + \sqrt b }}\) lập thành một cấp số cộng. Mệnh đề nào dưới đây là đúng ?
Dân số của thành phố A hiện nay là $3$ triệu người. Biết rằng tỉ lệ tăng dân số hàng năm của thành phố A là $2\% $. Dân số của thành phố A sau $3$ năm nữa sẽ là:
Trong năm đầu tiên đi làm, anh A được nhận lương là 10 triệu đồng mỗi tháng. Cứ hết một năm, anh A lại được tăng lương, mỗi tháng năm sau tăng 12% so với mỗi tháng năm trước. Mỗi khi lĩnh lương anh A đều cất đi phần lương tăng so với năm ngay trước để tiết kiệm mua ô tô. Hỏi sau ít nhất bao nhiêu năm thì anh A mua được ô tô giá 500 triệu biết rằng anh A được gia đình hỗ trợ 32% giá trị chiếc xe?
Tính tổng \({S_n} = 1 + 11 + 111 + ... + 11...11\) (có $10$ chữ số $1$)
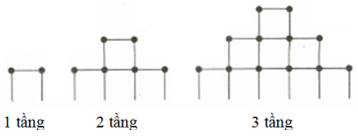
Bạn An chơi trò chơi xếp các que diêm thành tháp theo qui tắc thể hiện như hình vẽ. Để xếp được tháp có $10$ tầng thì bạn An cần đúng bao nhiêu que diêm?
Ba số dương lập thành cấp số nhân, tích của số hạng thứ nhất và số hạng thứ ba bằng $36$. Một cấp số cộng có $n$ số hạng, công sai $d = 4$, tổng các số hạng bằng $510$. Biết số hạng đầu của cấp số cộng bằng số hạng thứ 2 của cấp số nhân. Khi đó $n$ bằng:
Chu kì bán rã của nguyên tố phóng xạ poloni $210$ là $138$ ngày (nghĩa là sau $138$ ngày khối lượng của nguyên tố đó chỉ còn một nửa). Khi đó khối lượng còn lại của $20$ gam poloni $210$ sau $7314$ ngày là:
Cho dãy số \(\left( {{u_n}} \right)\) thỏa mãn \({u_1} = \sqrt 2 \) và \({u_{n + 1}} = \sqrt {2 + {u_n}} \) với mọi \(n \ge 1\). Tìm \({u_{2018}}\).

