I. Dạng 1: Tìm số điểm dao động cực đại – cực tiểu giữa hai nguồn
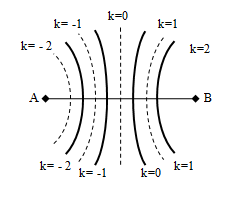
- Hai nguồn cùng pha:
( \({{\bf{S}}_{\bf{1}}}{{\bf{S}}_{\bf{2}}} = {\bf{AB}}{\rm{ }} = \ell \))
Số Cực đại giữa hai nguồn: \( - \dfrac{l}{\lambda } < k < \dfrac{l}{\lambda }\) và \(k \in Z\)
Số Cực tiểu giữa hai nguồn: \( - \dfrac{l}{\lambda } - \dfrac{1}{2} < k < \dfrac{l}{\lambda } - \dfrac{1}{2}\) và \(k \in Z\) . hay \( - \dfrac{l}{\lambda } < k + 0,5 < + \dfrac{l}{\lambda }{\rm{ (k}} \in {\rm{Z)}}\)
- Hai nguồn ngược pha: \(\Delta \varphi = {\varphi _1} - {\varphi _2} = \pi \)
Điểm dao động cực đại: \({d_1}-{\rm{ }}{d_2} = \left( {2k + 1} \right)\dfrac{\lambda }{2}{\rm{ }}(k \in Z)\)
Số đường hoặc số điểm dao động cực đại (không tính hai nguồn):
Số Cực đại: \( - \dfrac{l}{\lambda } - \dfrac{1}{2} < k < \dfrac{l}{\lambda } - \dfrac{1}{2}\) Hay \( - \dfrac{l}{\lambda } < k + 0,5 < + \dfrac{l}{\lambda }{\rm{ (k}} \in {\rm{Z)}}\)
Điểm dao động cực tiểu (không dao động): \({d_1}-{\rm{ }}{d_2} = k\lambda {\rm{ }}(k \in Z)\)
Số đường hoặc số điểm dao động cực tiểu (không tính hai nguồn):
Số Cực tiểu: \( - \dfrac{l}{\lambda } < k < + \dfrac{l}{\lambda }{\rm{ (k}} \in {\rm{Z)}}\)
- Hai nguồn vuông pha: \(\Delta \varphi = \left( {2k + 1} \right)\dfrac{\pi }{2}\)
+ Phương trình hai nguồn kết hợp: \({u_A} = A\cos \omega t\);\({u_B} = A\cos (\omega t + \dfrac{\pi }{2})\).
+ Phương trình sóng tổng hợp tại M: \(u = 2A\cos \left( {\dfrac{\pi }{\lambda }\left( {{d_2} - {d_1}} \right) - \dfrac{\pi }{4}} \right)\cos \left( {\omega t - \dfrac{\pi }{\lambda }\left( {{d_1} + {d_2}} \right) + \dfrac{\pi }{4}} \right)\)
+ Độ lệch pha của hai sóng thành phần tại M: \(\Delta \varphi = \dfrac{{2\pi }}{\lambda }\left( {{d_2} - {d_1}} \right) - \dfrac{\pi }{2}\)
+ Biên độ sóng tổng hợp: \(u = 2A\left| {\cos \left( {\dfrac{\pi }{\lambda }\left( {{d_2} - {d_1}} \right) - \dfrac{\pi }{4}} \right)} \right|{A_M} = \)
* Số Cực đại: \( - \dfrac{l}{\lambda } + \dfrac{1}{4} < k < + \dfrac{l}{\lambda } + \dfrac{1}{4}{\rm{ (k}} \in {\rm{Z)}}\)
* Số Cực tiểu:\( - \dfrac{l}{\lambda } - \dfrac{1}{4} < k < + \dfrac{l}{\lambda } - \dfrac{1}{4}{\rm{ (k}} \in {\rm{Z)}}\) Hay \( - \dfrac{l}{\lambda } < k + 0,25 < + \dfrac{l}{\lambda }{\rm{ (k}} \in {\rm{Z)}}\)
Nhận xét: số điểm cực đại và cực tiểu trên đoạn AB là bằng nhau nên có thể dùng 1 công thức là đủ
=> Số giá trị nguyên của k thoả mãn các biểu thức trên là số đường cần tìm.
II. Dạng 2: Số điểm dao động với biên độ cực đại – cực tiểu giữa hai điểm bất kì
Số cực đại và cực tiểu trên đoạn thẳng nối hai điểm M và N trong vùng có giao thoa (M gần S1 hơn S2 còn N thì xa S1 hơn S2) là số các giá trị của k \((k \in Z)\) tính theo công thức sau ( không tính hai nguồn):
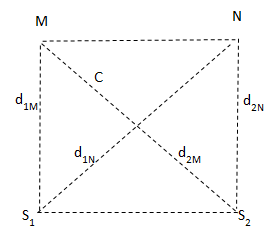
- Dùng công thức:
Số Cực đại: \(\dfrac{{{S_1}M - {S_2}M}}{\lambda } + \dfrac{{\Delta \varphi }}{2} < k < \dfrac{{{S_1}N - {S_2}N}}{\lambda } + \dfrac{{\Delta \varphi }}{2}\)
Số Cực tiểu: \(\dfrac{{{S_1}M - {S_2}M}}{\lambda } - \dfrac{1}{2} + \dfrac{{\Delta \varphi }}{2} < k < \dfrac{{{S_1}N - {S_2}N}}{\lambda } - \dfrac{1}{2} + \dfrac{{\Delta \varphi }}{2}\)
=> Với các nguồn:
+ Hai nguồn dao động cùng pha: ( $\Delta \varphi = k2\pi$)
* Số Cực đại: \(\dfrac{{{S_1}M - {S_2}M}}{\lambda } < {\rm{ }}k{\rm{ }} < \dfrac{{{S_1}N - {S_2}N}}{\lambda }\)
* Số Cực tiểu: \(\dfrac{{{S_1}M - {S_2}M}}{\lambda } - \dfrac{1}{2} < {\rm{ }}k{\rm{ }} < \dfrac{{{S_1}N - {S_2}N}}{\lambda } - \dfrac{1}{2}\)
+ Hai nguồn dao động ngược pha: \(\Delta \varphi = \left( {{\bf{2k}} + {\bf{1}}} \right)\pi \)
* Số Cực đại: \(\dfrac{{{S_1}M - {S_2}M}}{\lambda } + \dfrac{1}{2} < {\rm{ }}k{\rm{ }} < \dfrac{{{S_1}N - {S_2}N}}{\lambda } + \dfrac{1}{2}\)
* Số Cực tiểu: \(\dfrac{{{S_1}M - {S_2}M}}{\lambda } < {\rm{ }}k{\rm{ }} < \dfrac{{{S_1}N - {S_2}N}}{\lambda }\)
+ Hai nguồn dao động vuông pha: \(\Delta \varphi = \dfrac{{\left( {{\bf{2k}} + {\bf{1}}} \right)\pi }}{2}\)
* Số Cực đại: \(\dfrac{{{S_1}M - {S_2}M}}{\lambda } + \dfrac{1}{4} < {\rm{ }}k{\rm{ }} < \dfrac{{{S_1}N - {S_2}N}}{\lambda } + \dfrac{1}{4}\)
* Số Cực tiểu: \(\dfrac{{{S_1}M - {S_2}M}}{\lambda } - \dfrac{1}{4} < {\rm{ }}k{\rm{ }} < \dfrac{{{S_1}N - {S_2}N}}{\lambda } - \dfrac{1}{4}\)
Nhận xét: số điểm cực đại và cực tiểu trên đoạn AB là bằng nhau nên có thể dùng 1 công thức
Số giá trị nguyên của k thoả mãn các biểu thức trên là số điểm( đường) cần tìm
