I. Thấu kính
- Định nghĩa:
Thấu kính là một khối chất trong suốt giới hạn bởi hai mặt cầu hoặc một mặt phẳng và một mặt cầu.
Có 2 loại:
- Thấu kính rìa (mép) mỏng:
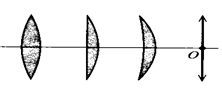
- Thấu kính rìa (mép) dày:

- Trong không khí, thấu kính rìa mỏng là thấu kính hội tụ, thấu kính rìa dày là thấu kính phân kỳ.
- Thấu kính hội tụ làm hội tụ chùm tia sáng tới, thấu kính phân kì làm phân kì chùm tia sáng tới
II. Đường đi của tia sáng qua thấu kính
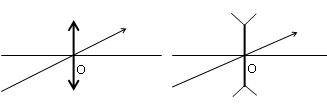
- Tia sáng qua quang tâm O thì truyền thẳng
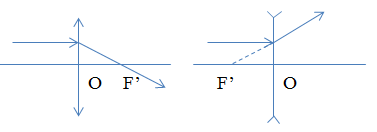
- Tia sáng song song với trục chính cho tia ló (hoặc đường kéo dài) qua tiêu điểm ảnh chính
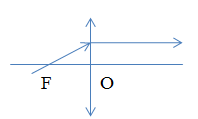
- Tia sáng (hoặc đường kéo dài) qua tiêu điểm vật chính cho tia ló song song trục chính.
III. Vị trí vật - ảnh

- Với thấu kính hội tụ:
+ vật thật chỉ cho ảnh ảo nếu trong khoảng OF, còn lại cho ảnh thật, ảnh thật thì ngược chiều, còn ảo thì cùng chiều.
+ về độ lớn của ảnh: độ lớn ảnh tăng dần đến ∞ rồi giảm.
IV. Tiêu cự - Mặt phẳng tiêu diện
- Tiêu cự: | f | = OF
Quy ước: Thấu kính hội tụ thì f > 0, thấu kính phân kỳ thì f < 0.
- Tiêu diện:
+ Tiêu diện vật: mặt phẳng vuông góc với trục chính tại tiêu điểm vật
+ Tiêu diện ảnh: mặt phẳng vuông góc với trục chính tại tiêu điểm ảnh
- Tiêu điểm phụ:
+ Các tiêu điểm vật phụ ở trên mặt phẳng tiêu diện vật vuông góc với trục chính tại F.
+ Các tiêu điểm ảnh phụ ở trên mặt phẳng tiêu diện ảnh vuông góc với trục chính tại F’.
V. Độ tụ
- Độ tụ của thấu kính: D=1f
Đơn vị: trong hệ SI, đơn vị của độ tụ là điôp, tiêu cự f tính bằng mét.
Với thấu kính hội tụ D>0 , thấu kính phân kì D<0
- Công thức độ tụ tính theo bán kính hai mặt cầu: D=1f=(nnmt−1)(1R1+1R2)
Quy ước: mặt cầu lồi thì R>0, mặt cầu lõm thì R<0, mặt phẳng thì R=∞.
VI. Các công thức về thấu kính
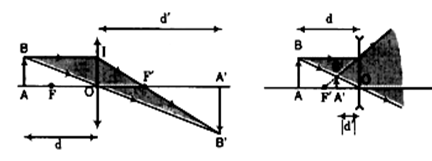
- Quy ước: {¯OA=d¯OA′=d′¯OF′=f
+ Vật thật thì d > 0
+ Vật ảo thì d < 0
+ Ảnh thật thì d’ > 0
+ Ảnh ảo thì d’ <0
- Công thức về vị trí ảnh - vật : 1f=1d+1d′
- Công thức về độ phóng đại ảnh của vật qua thấu kính: k=−d′d=¯A′B′¯AB
Trong đó:
+ k > 0: thì ảnh và vật cùng chiều, trái tính chất thật, ảo.
+ k < 0: thì ảnh và vật ngược chiều, cùng tính chất thật, ảo.
- Hệ quả: d′=d.fd−f;d=d′.fd′−f;f=d.d′d+d′;k=−d′d=ff−d=f−d′f
- Công thức khoảng cách vật và ảnh: L=|d+d′|
Trong đó:
+ nếu vật thật qua thấu kính cho ảnh thật thì L > 0
+ nếu vật ảo qua thấu kính cho ảnh ảo thì L < 0
- Tỉ lệ về diện tích của vật và ảnh: S=(¯A′B′¯AB)2=k2
- Nếu vật AB tại hai vị trí cho hai ảnh khác nhau A1B1 và A2B2 thì: (AB)2 = (A1B1)2.(A2B2)2
- Điều kiện để vật thật qua thấu kính cho ảnh thật là: L ³ 4.f
- Vật AB đặt cách màn một khoảng L, có hai vị trí của thấu kính cách nhau l sao cho AB qua thấu kính cho ảnh rõ nét trên màn thì tiêu cự thấu kính tính theo công thức: f=L2−l24.L
- Nếu có các thấu kính ghép sát nhau thì công thức tính độ tụ tương đương là: D=D1+D2+...

