I. Lý thuyết con lắc lò xo
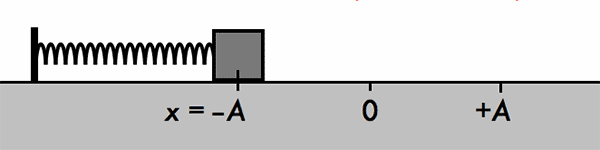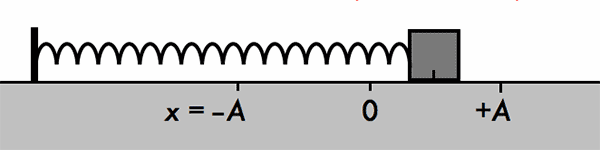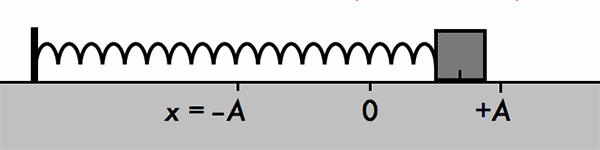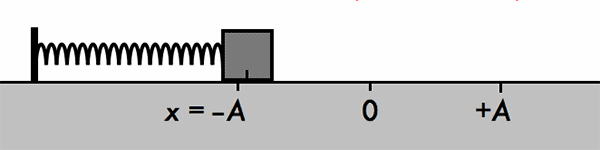
- Con lắc lò xo gồm một vật nhỏ có khối lượng m gắn vào đầu một lò xo có độ cứng k và khối lượng không đáng kể.
- Phương trình dao động:
+ Li độ: \(x = A\cos \left( {\omega t + \varphi } \right)\)
+ Vận tốc: \(v = x' = \omega A\cos \left( {\omega t + \varphi + \dfrac{\pi }{2}} \right)\)
+ Gia tốc: \(a = {\omega ^2}A\cos \left( {\omega t + \varphi + \pi } \right)\)
- Chu kì, tần số, tần số góc:
\(\omega = \sqrt {\dfrac{k}{m}} \),\(T = \dfrac{{2\pi }}{\omega } = 2\pi \sqrt {\dfrac{m}{k}} \), \(f = \dfrac{\omega }{{2\pi }} = \dfrac{1}{{2\pi }}\sqrt {\dfrac{k}{m}} \)
II. Năng lượng của con lắc lò xo
- Cơ năng:
\({\rm{W}} = {{\rm{W}}_d} + {{\rm{W}}_t} = \dfrac{1}{2}m{v^2} + \dfrac{1}{2}k{{\rm{x}}^2} = \dfrac{1}{2}m{\omega ^2}A = \dfrac{1}{2}k{A^2}\)
- Thế năng:
\({{\rm{W}}_t} = \dfrac{1}{2}k{{\rm{x}}^2} = {\rm{W}} - {{\rm{W}}_d} = \dfrac{1}{2}k{A^2} - \dfrac{1}{2}m{v^2}\)
- Động năng:
\({{\rm{W}}_d} = \dfrac{1}{2}m{v^2} = {\rm{W}} - {{\rm{W}}_t} = \dfrac{1}{2}k{A^2} - \dfrac{1}{2}k{{\rm{x}}^2}\)
- Trong suốt quá trình dao động, động năng và thế năng của con lắc lò xo biến thiên tuần hoàn với chu kì T/2, còn cơ năng của vật được bảo toàn.

