I. Lý thuyết sóng cơ
- Sóng cơ: là dao động cơ lan truyền trong một môi trường.
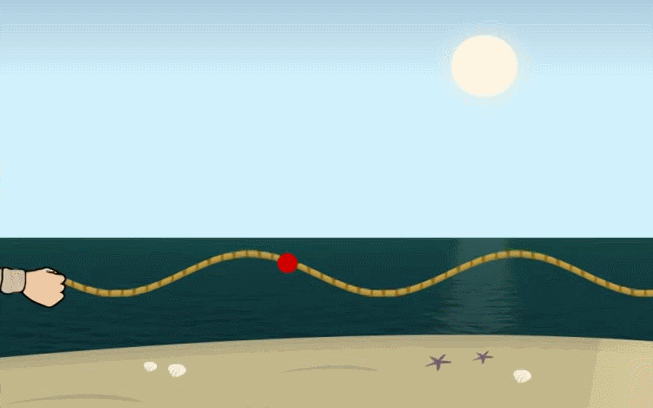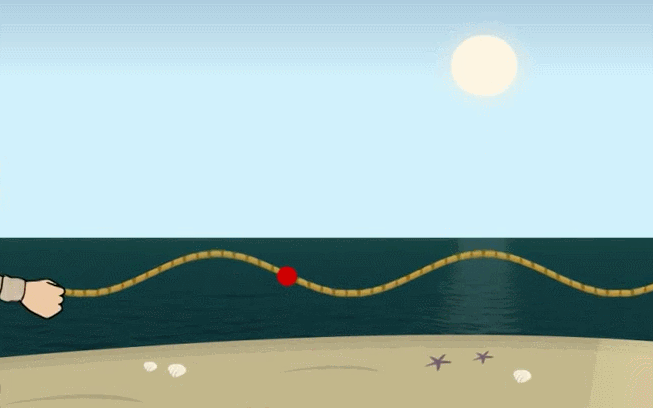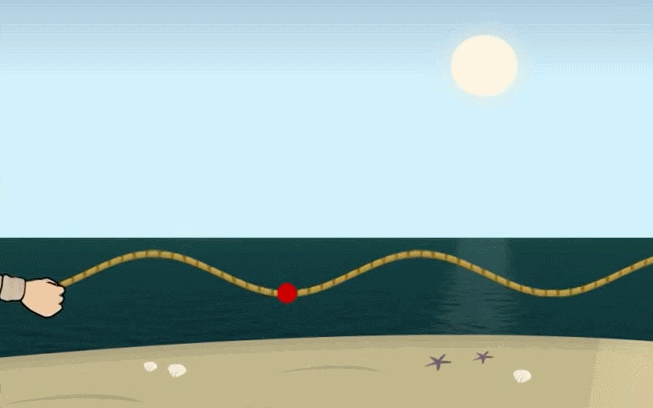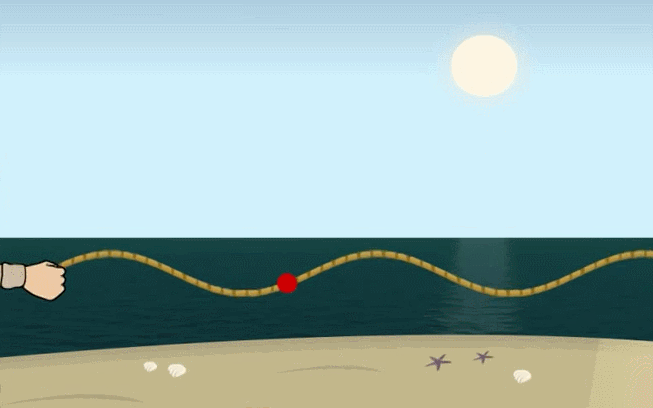
+ Sóng ngang: là sóng trong đó các phần tử của môi trường dao động theo phương vuông góc với phương truyền sóng. Sóng ngang truyền trong chất rắn và bề mặt chất lỏng.
+ Sóng dọc: là sóng trong đó các phần tử của môi trường dao động theo phương trùng với phương truyền sóng. Sóng dọc truyền trong taát cả các môi trường rắn, lỏng, khí.
- Phương trình sóng:
uM=Acosω(t−xv)=Acos(ωt−2πxλ)
II. Các đại lượng đặc trưng của sóng cơ
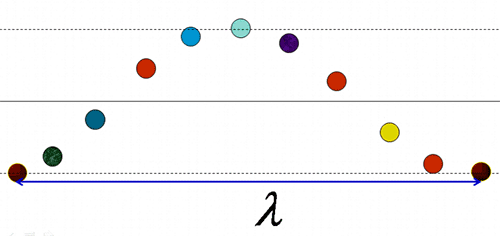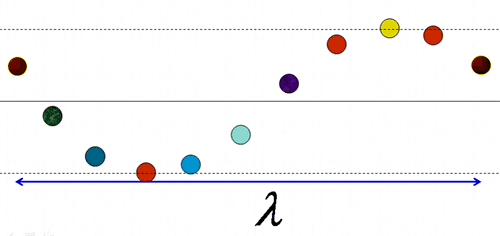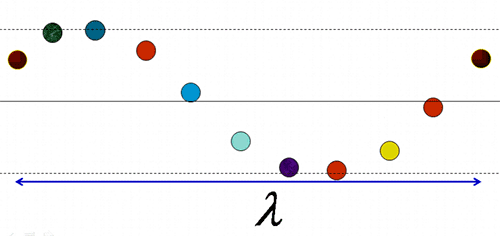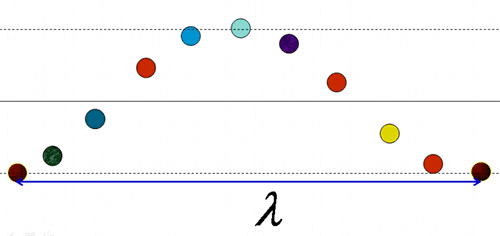
- Chu kì (T), vận tốc (v), tần số (f), bước sóng (λ) liên hệ với nhau:
f=1T;λ=vT;v=ΔsΔt với Δs là quãng đường sóng truyền trong thời gian Δt
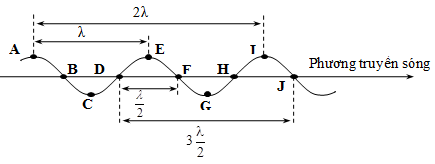
- Quan sát hình ảnh sóng có n ngọn sóng liên tiếp thì có (n-1) bước sóng. Hoặc quan sát thấy từ ngọn sóng thứ n đến ngọn sóng thứ m (m > n) có chiều dài l thì bước sóng: λ=lm−n
- Số lần nhô lên mặt nước là N trong khoảng thời gian t giây thì T=tN−1
- Độ lệch pha giữa hai điểm cách nguồn một khoảng xM, xN:
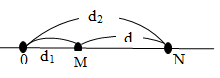
ΔφMN=ωxN−xMv=2πxN−xMλ=2πdλ
trong đó: xN−xM=d
+ Nếu 2 điểm M và N dao động cùng pha thì:
ΔφMN=2kπ⇔d=kλ(k∈Z)
+ Nếu 2 điểm M và N dao động ngược pha thì:
ΔφMN=(2k+1)π⇔d=(2k+1)λ2(k∈Z)
+ Nếu 2 điểm M và N dao động vuông pha thì:
φMN=(2k+1)π2⇔d=(2k+1)λ4

