I. Thí nghiệm về tán sắc ánh sáng
- Định luật khúc xạ ánh sáng:
sini=nsinrsini′=nsinr′A=r+r′D=i+i′−(r+r′)=i+i′−A
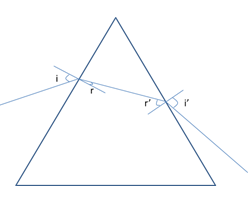
Trường hợp: Góc chiết quang A nhỏ
i=nri′=nr′A=r+r′D=i+i′−(r+r′)=(n−1)A
- Thí nghiệm:
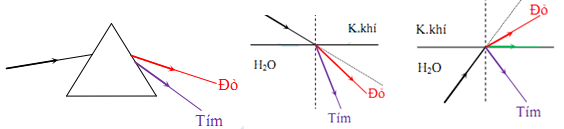
Kết luận:
- Sự tán sắc ánh sáng là sự phân tách một chùm ánh sáng phức tạp thành các chùm sáng đơn sắc.
- Ánh sáng đỏ bị lệch ít nhất, ánh sáng tím bị lệch nhiều nhất.
Trường hợp: khi chiếu đến lăng kính có góc chiết quang nhỏ
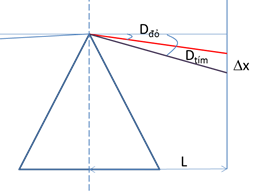
tanDd=xdL,tanDt=xtL
∆x: Độ rộng phổ
Vì A≪ →{Dd≪Dt≪→tanD≈sinD≈D
Δx=xt−xd=(nt−1)AL−(nd−1)AL=(nt−nd)LA
II. Giải thích hiện tượng tán sắc ánh sáng
- Ánh sáng đơn sắc: là ánh sáng không bị tán sắc khi đi qua lăng kính
- Ánh sáng trắng: là hỗn hợp của ánh sáng đơn sắc có màu từ Đỏ đến Tím
- Vì ánh sáng trắng là tập hợp của vô số ánh sáng đơn sắc
- Chiết suất của thủy tinh đối với các ánh sáng đơn sắc có màu khác nhau thì khác nhau
- n=cv
với:
+ n: Chiết suất tuyệt đối của một môi trường
+ c: Vận tốc ánh sáng trong chân không
+ v: Vận tốc ánh sáng trong môi trường
- Vận tốc truyền ánh sáng trong các môi trường của ánh sáng đơn sắc là khác nhau:
+ vđỏ > vcam > vvàng > vlục > vlam > vchàm > vtím
+ nđỏ < ncam < nvàng < nlục < nlam < nchàm < ntím
+ Dđỏ < Dcam < Dvàng < Dlục < Dlam < Dchàm <Dtím
- Khi ánh sáng truyền từ môi trường này sang môi trường khác thì tần số không thay đổi, bước sóng và vận tốc ánh sáng thay đổi
- Bước sóng trong môi trường có chiết suất n: λ=λckn
* Ứng dụng của sự tán sắc ánh sáng:
- Giải thích các hiện tượng trong tự nhiên
- Phân tích ánh sáng

