Chọn phát biểu đúng
A – đúng
B – sai vì: Hai dòng điện thẳng song song cùng chiều thì hút nhau
C - sai vì Hai dòng điện thẳng song song ngược chiều thì đẩy nhau
D – sai vì: Lực tương tác giữa hai dòng điện thẳng song song có độ lớn tỉ lệ thuận với cường độ của hai dòng điện.
Khi giảm đồng thời cường độ dòng điện trong cả hai dây dẫn thẳng song song lên \(3\) lần thì lực từ tác dụng lên một đơn vị dài của mỗi dây sẽ :
Ta có: \(F = {2.10^{ - 7}}\dfrac{{{I_1}{I_2}}}{r}\)
=> Khi I1 và I2 đều giảm 3 lần thì \(F' = {2.10^{ - 7}}\dfrac{{\dfrac{{{I_1}}}{3}\dfrac{{{I_2}}}{3}}}{r} = \dfrac{F}{9}\)
=> F giảm \(9\) lần
Hai dây dẫn thẳng dài đặt song song với nhau và cách nhau \(10cm\) đặt trong không khí. Dòng điện chạy trong dây dẫn có cường độ \({I_1} = 2A\), \({I_2} = 5A\). Lực từ tác dụng lên một đoạn có chiều dài \(0,2m\) của mỗi dây là:
Ta có:
Lực từ tác dụng lên đoạn dây có chiều dài \(0,2m\) của mỗi dây là: \(F = {2.10^{ - 7}}\dfrac{{{I_1}{I_2}}}{r}l = {2.10^{ - 7}}\dfrac{{2.5}}{{0,1}}0,2 = {4.10^{ - 6}}N\)
Hai vòng tròn dây dẫn đặt cách nhau một khoảng rất nhỏ. Vòng dây dẫn được giữ cố định. Vòng trên được nối với một đòn cân. Khi có 2 dòng điện có cường độ bằng nhau vào 2 dây dẫn thì chúng hút nhau. Đặt thêm một quả cân khối lượng \(0,2g\) vào đĩa cân bên kia thì cân trở lại thăng bằng và lúc đó hai vòng dây cách nhau \(1mm\). Xác định cường độ dòng điện trong mỗi vòng dây. Biết bán kính mỗi vòng dây là \(4cm\). Lấy \(g{\rm{ }} = {\rm{ }}10m/{s^2}\) .
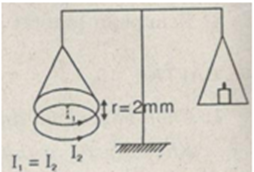
Cân nằm thăng bằng khi: F = P = mg (1)
Ta có, lực từ tác dụng lên mỗi đơn vị chiều dài của vòng dây:
\({F_0} = \dfrac{F}{{2\pi R}} = {2.10^{ - 7}}\dfrac{{{I_1}{I_2}}}{r} = {2.10^{ - 7}}\dfrac{{{I^2}}}{r}{\rm{ (2)}}\)
Từ (1) và (2), ta có:
\(\begin{array}{l}{2.10^{ - 7}}\dfrac{{{I^2}}}{r} = \dfrac{{mg}}{{2\pi R}}\\ \to I = \sqrt {\dfrac{{mg{\rm{r}}}}{{4\pi {{.10}^{ - 7}}.R}}} = \sqrt {\dfrac{{0,{{2.10}^{ - 3}}{\rm{.10}}{\rm{.1}}{\rm{.1}}{{\rm{0}}^{ - 3}}}}{{4\pi {{.10}^{ - 7}}{{.4.10}^{ - 2}}}}} = 6,31A\end{array}\)
Ba dòng điện cùng chiều, cùng cường độ \(I = 10A\) chạy qua ba dây dẫn thẳng đặt đồng phẳng và dài vô hạn. Biết rằng khoảng cách giữa dây 1 và dây 2 là \(10cm\), giữa dây 2 và dây 3 là \(5cm\), giữa dây 1 và dây 3 là \(15cm\). Xác định lực từ do dây 1 và dây 2 tác dụng lên dây 3
Xác định lực từ do các dòng \({I_1}\) và \({I_2}\) tác dụng lên \({I_3}\), ta có:

Trong đó:
\({F_{13}} = {2.10^{ - 7}}\dfrac{{{I_1}{I_3}}}{{{r_{13}}}} = {2.10^{ - 7}}\dfrac{{10.10}}{{0,15}} = \dfrac{4}{3}{.10^{ - 4}}N\)
\({F_{23}} = {2.10^{ - 7}}\dfrac{{{I_2}{I_3}}}{{{r_{23}}}} = {2.10^{ - 7}}\dfrac{{10.10}}{{0,05}} = {4.10^{ - 4}}N\)
Lực từ do các dòng \({I_1}\) và \({I_2}\) tác dụng lên \({I_3}\) là: \(\overrightarrow F = \overrightarrow {{F_{13}}} + \overrightarrow {{F_{23}}} \)
Ta có: \(\overrightarrow {{F_{13}}} \uparrow \uparrow \overrightarrow {{F_{23}}} \Rightarrow F = {F_{13}} + {F_{23}} = \dfrac{4}{3}{.10^{ - 4}} + {4.10^{ - 4}} = \dfrac{{16}}{3}{.10^{ - 4}}N\)
Ba dòng điện cùng chiều, cùng cường độ \(I = 10A\) chạy qua ba dây dẫn thẳng đặt đồng phẳng và dài vô hạn. Biết rằng khoảng cách giữa dây 1 và dây 2 là \(10cm\), giữa dây 2 và dây 3 là \(5cm\), giữa dây 1 và dây 3 là \(15cm\). Xác định lực từ do dây 1 và dây 3 tác dụng lên dây 2
Xác định lực từ do các dòng \({I_1}\) và \({I_3}\) tác dụng lên \({I_2}\), ta có:
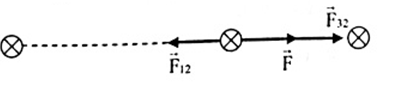
Trong đó:
\({F_{12}} = {2.10^{ - 7}}\dfrac{{{I_1}{I_2}}}{{{r_{12}}}} = {2.10^{ - 7}}\dfrac{{10.10}}{{0,1}} = {2.10^{ - 4}}N\)
\({F_{32}} = {2.10^{ - 7}}\dfrac{{{I_3}{I_2}}}{{{r_{32}}}} = {2.10^{ - 7}}\dfrac{{10.10}}{{0,05}} = {4.10^{ - 4}}N\)
Lực từ do các dòng \({I_1}\) và \({I_2}\) tác dụng lên \({I_3}\) là: \(\overrightarrow F = \overrightarrow {{F_{13}}} + \overrightarrow {{F_{23}}} \)
Ta có: \(\overrightarrow {{F_{12}}} \uparrow \downarrow \overrightarrow {{F_{32}}} \Rightarrow F = \left| {{F_{12}} - {F_{32}}} \right| = {4.10^{ - 4}} - {2.10^{ - 4}} = {2.10^{ - 4}}N\)
Ba dây dẫn thẳng dài song song cách đều nhau một khoảng \(a = 10cm\) như hình vẽ. Cường độ dòng điện \({I_1} = 25A\), \({I_2} = {I_3} = 10A\). Xác độ lớn của lực từ tác dụng lên \(1m\) của dây \({I_1}\)?
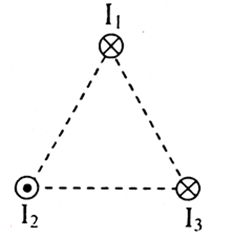
Ta có, lực do các dòng \({I_2},{I_3}\) tác dụng lên \({I_1}\)
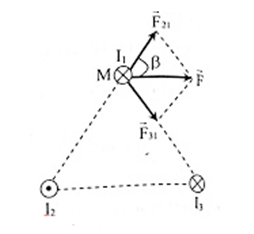
Ta có:
\({r_{21}} = {r_{31}} = a = 10cm = 0,1m\)
\({I_2} = {I_3} = 10A\)
\({F_{21}} = {2.10^{ - 7}}\dfrac{{{I_2}{I_1}}}{{{r_{21}}}}.l = {2.10^{ - 7}}.\dfrac{{10.25}}{{0,1}} = {5.10^{ - 4}}N\)
\({F_{31}} = {2.10^{ - 7}}\dfrac{{{I_3}{I_1}}}{{{r_{31}}}}l = {2.10^{ - 7}}\dfrac{{10.25}}{{0,1}}.1 = {5.10^{ - 4}}N = {F_{21}}\)
Lực tổng hợp do các dòng \({I_2},{I_3}\) tác dụng lên \({I_1}\): \(\overrightarrow F = \overrightarrow {{F_{21}}} + \overrightarrow {{F_{31}}} \)
Do \(\Delta {I_1}{I_2}{I_3}\) là tam giác đều \( \Rightarrow \widehat {{I_3}{I_1}{I_2}} = {60^0} = \beta \)
Từ hình, ta có: \(F = 2{F_{21}}cos\beta = {2.5.10^{ - 4}}.cos{60^0} = {5.10^{ - 4}}N\)
Một dây dẫn mang dòng điện \({I_1} = 5A\) đặt tại điểm A. Tại điểm B cách A \(5cm\) người ta đặt một dòng điện \({I_2}\) ngược chiều với \({I_1}\). Biết lực tương tác giữa hai dây dẫn là \(2,{5.10^{ - 4}}N\). Giá trị của \({I_2}\) là:

Ta có, lực tương tác giữa hai dây dẫn: \(F = {2.10^{ - 7}}\dfrac{{{I_1}{I_2}}}{r}\)
\( \Rightarrow \) Cường độ dòng điện \({I_2} = \dfrac{{F.r}}{{{{2.10}^{ - 7}}.{I_1}}} = \dfrac{{2,{{5.10}^{ - 4}}.0,05}}{{{{2.10}^{ - 7}}.5}} = 12,5A\)
Một dây dẫn mang dòng điện \({I_1} = 5A\) đặt tại điểm A. Tại điểm B cách A \(5cm\) người ta đặt một dòng điện \({I_2}\) ngược chiều với \({I_1}\). Biết \({I_2} = 10A\), hãy xác định lực tương tác giữa chúng?
Ta có, 2 dòng I1 và I2 ngược chiều nhau => lực tương tác là lực đẩy
\(F = {2.10^{ - 7}}\dfrac{{{I_1}{I_2}}}{r} = {2.10^{ - 7}}\dfrac{{5.10}}{{0,05}} = {2.10^{ - 4}}N\)
Hai dây dẫn đặt cách nhau \(2cm\) trong không khí, dòng điện trong 2 dây có cùng giá trị cường độ, lực tương tác từ giữa hai dây là lực hút và có độ lớn \(F = 2,{5.10^{ - 4}}N\). Hai dòng điện trên cùng chiều hay ngược chiều và cường độ dòng điện trong mỗi dây có giá trị là bao nhiêu?
Ta có:
+ Lực tương tác giữa hai dây là lực hút => Dòng điện trong hai dây cùng chiều với nhau
+ Lực tương tác giữa hai dây: \(F = {2.10^{ - 7}}\dfrac{{{I_1}{I_2}}}{r}\)
Lại có \({I_1} = {I_2} = I\)
Ta suy ra:
\(\begin{array}{l}F = {2.10^{ - 7}}\dfrac{{{I^2}}}{r}\\ \Rightarrow I = \sqrt {\dfrac{{F.r}}{{{{2.10}^{ - 7}}}}} = \sqrt {\dfrac{{2,{{5.10}^{ - 4}}.0,02}}{{{{2.10}^{ - 7}}}}} = 5A\end{array}\)
Ba dây dẫn thẳng dài được đặt song song trong cùng mặt phẳng thẳng đứng như hình vẽ. Dây 1 và dây 3 được giữ cố định có dòng điện chạy xuống và I1 > I3 . Xác định chiều của dòng I2 nếu dây 2 bị dịch sang trái?
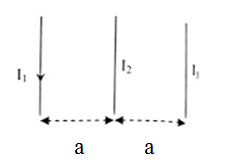
Ta có:
\({F_{12}} = {2.10^{ - 7}}\dfrac{{{I_1}{I_2}}}{a}\)
\({F_{32}} = {2.10^{ - 7}}\dfrac{{{I_3}{I_2}}}{a}\)
\({I_1} > {I_3} \to {F_{12}} > {F_{23}}\)
Muốn dây 2 dịch sang trái thì F12 phải hướng sang trái
=> F12 là lực hút => I1 và I2 cùng chiều nhau
=> I2 hướng xuống
Hai dòng điện vô hạn đặt song song cách nhau \(20cm\) mang hai dòng điện cùng chiều \({I_1} = 20A;{I_2} = 30A\) . Cần đặt dòng \({I_3}\) cách \({I_1},{\rm{ }}{I_2}\) một khoảng bao nhiêu để lực từ tác dụng lên \({I_3}\) bằng 0?
Ta có:
\(\overrightarrow {{F_3}} = \overrightarrow {{F_{13}}} + \overrightarrow {{F_{23}}} = \overrightarrow 0 \to \overrightarrow {{F_{13}}} = - \overrightarrow {{F_{23}}} \)
=> I1, I2 cùng chiều và \({F_{13}} = {F_{23}}\)
=> I3 phải nằm giữa I1 và I2
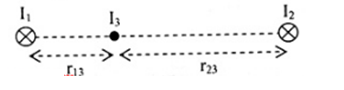
+ \({F_{13}} = {F_{23}} \to \dfrac{{{I_1}}}{{{r_{13}}}} = \dfrac{{{I_2}}}{{{r_{23}}}} \Leftrightarrow \dfrac{{20}}{{{r_{13}}}} = \dfrac{{30}}{{{r_{23}}}} \to {r_{13}} = \dfrac{2}{3}{{\rm{r}}_{23}}\)
Mặt khác, ta có: \({r_{13}} + {r_{23}} = 20cm\)
\( \to \left\{ \begin{array}{l}{r_{13}} = 8cm\\{r_{23}} = 12cm\end{array} \right.\)
Ba dây dẫn thẳng dài song song cách đều nhau một khoảng \(a = 10cm\) như hình vẽ. Cường độ dòng điện \({I_1} = 25A,{I_2} = {I_3} = 10A\). Xác định phương, chiều và độ lớn của lực từ tác dụng lên 1m của dây \({I_1}\)
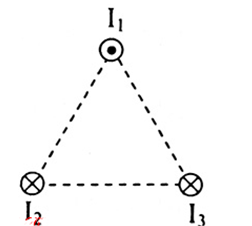
Ta có, lực từ do các dòng \({I_2},{I_3}\) tác dụng lên \({I_1}\)
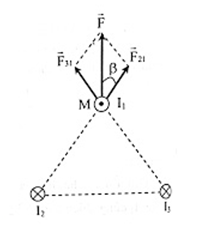
Ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}{r_{21}} = {r_{31}} = a = 10cm = 0,1m\\{I_2} = {I_3} = 10A\end{array} \right.\\ \Rightarrow {F_{21}} = {F_{31}} = {2.10^{ - 7}}\dfrac{{{I_2}{I_1}}}{{{r_{21}}}} = {2.10^{ - 7}}\dfrac{{10.25}}{{0,1}} = {5.10^{ - 4}}N\end{array}\)
Lực từ tổng hợp tác dụng lên \({I_1}\) là \(\overrightarrow F = \overrightarrow {{F_{21}}} + \overrightarrow {{F_{31}}} \)
Từ hình, ta có:
\(F = 2{F_{21}}cos\beta \)
Mặt khác, ta có: \(\Delta {I_1}{I_2}{I_3}\) là tam giác đều
\(\begin{array}{l} \Rightarrow \widehat {{I_2}{I_1}{I_3}} = {60^0} \Rightarrow \beta = \dfrac{{{{60}^0}}}{2} = {30^0}\\ \Rightarrow F = 2{F_{21}}cos{30^0} = {2.5.10^{ - 4}}.cos{30^0} = 5\sqrt 3 {.10^{ - 4}}N\end{array}\)
Hai dòng điện thẳng đặt song song cách nhau 30cm mang hai dòng điện cùng chiều \({I_1} = {I_2} = 10A\). Dòng thứ 3 đặt song song với hai dòng điện trên và thuộc mặt phẳng trung trực của 2 dòng I1 và I2. Biết \({I_3} = 10A\), ngược chiều với I1 và I3 cách mặt phẳng chứa (I1, I2) đoạn d = 15cm. Lực từ tác dụng lên 1m của dòng I3.
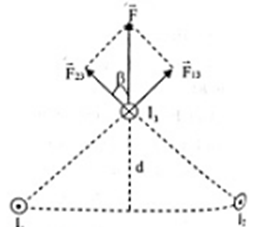
Ta có:
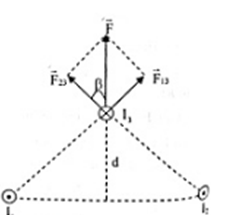
\(\begin{array}{l}{r_{13}} = {r_{23}} = \sqrt {{d^2} + \dfrac{{r_{12}^2}}{4}} = \sqrt {0,{{15}^2} + \dfrac{{0,{3^2}}}{4}} = 0,15\sqrt 2 m\\{I_1} = {I_2} \to {F_{13}} = {F_{23}} = {2.10^{ - 7}}\dfrac{{{I_1}{I_3}}}{{{r_{13}}}} = {2.10^{ - 7}}\dfrac{{10.10}}{{0,15.\sqrt 2 }} = \dfrac{{2\sqrt 2 }}{3}{.10^{ - 4}}N\\{\rm{cos}}\beta = \dfrac{d}{{{r_{23}}}} = \dfrac{1}{{\sqrt 2 }} \to \beta = {45^0}\\ \to F = 2{F_{23}}{\rm{cos4}}{{\rm{5}}^0} = 2.\dfrac{{2\sqrt 2 }}{3}{.10^{ - 4}}.\dfrac{{\sqrt 2 }}{2} = \dfrac{4}{3}{.10^{ - 4}}N\end{array}\)
Hai dòng điện thẳng đặt song song cách nhau 20cm mang hai dòng điện cùng chiều \({I_1} = {I_2} = 10A\). Dòng thứ 3 đặt song song với hai dòng điện trên và thuộc mặt phẳng trung trực của 2 dòng I1 và I2. Biết \({I_3} = 20A\), ngược chiều với I1 và I3 cách mặt phẳng chứa (I1, I2) đoạn d . d = ? đê lực từ tác dụng lên 1m của dòng I3 đạt giá trị cực đại?
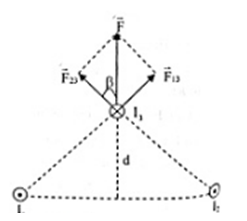
\(\begin{array}{l}{r_{13}} = {r_{23}} = \sqrt {{d^2} + \dfrac{{r_{12}^2}}{4}} \\{I_1} = {I_2}\\ \to {F_{13}} = {F_{23}} = {2.10^{ - 7}}\dfrac{{{I_1}{I_3}}}{{{r_{13}}}} = {2.10^{ - 7}}\dfrac{{10.20}}{{\sqrt {{d^2} + 0,01} }} = \dfrac{{{{4.10}^{ - 5}}}}{{\sqrt {{d^2} + 0,01} }}\\cos = \dfrac{d}{{{r_{23}}}} = \dfrac{d}{{\sqrt {{d^2} + 0,01} }}\\ \to F = 2{F_{23}}{\rm{cos}}\beta = {2.4.10^{ - 5}}\dfrac{1}{{\sqrt {{d^2} + 0,01} }}.\dfrac{d}{{\sqrt {{d^2} + 0,01} }} = \dfrac{{{{8.10}^{ - 5}}d}}{{{d^2} + 0,01}} = \dfrac{{{{8.10}^{ - 5}}}}{{d + \dfrac{{0,01}}{d}}}\end{array}\)
Ta có: Fmax khi: \({\left[ {d + \dfrac{{0,01}}{d}} \right]_{{\rm{min}}}}\)
Xét: \(d + \dfrac{{0,01}}{d} \ge 2\sqrt {d.\dfrac{{0,01}}{d}} = 0,2\)
Dấu “ = ” xảy ra khi: \(d = \dfrac{{0,01}}{d} \to d = 0,1m\)
Hai dây dẫn thẳng song song mang dòng điện I1 và I2 đặt cách nhau một khoảng r trong không khí. Trên mỗi đơn vị dài của mỗi dây chịu tác dụng của lực từ có độ lớn là:
\(\overrightarrow {{F_t}} \) trên một đơn vị của chiều dài: \(F = {2.10^{ - 7}}\frac{{{I_1}{I_2}}}{r}\)
Phát biểu nào sau đây không đúng?
A, B, D - đúng
C - sai vì Hai dòng điện thẳng song song ngược chiều thì đẩy nhau, cùng chiều hút nhau
Khi tăng đồng thời cường độ dòng điện trong cả hai dây dẫn thẳng song song lên 3 lần thì lực từ tác dùng lên một đơn vị dài của mỗi dây sẽ tăng lên
Ta có: \(F = {2.10^{ - 7}}\frac{{{I_1}{I_2}}}{r}\)
=> Khi I1 và I2 tăng lên 3 lần thì F tăng 3.3 = 9 lần
Hai dây dẫn thẳng dài đặt song song với nhau và cách nhau 10cm đặt trong không khí. Dòng điện chạy trong dây dẫn có cường độ I1 = 2A, I2 = 5A. Lực từ tác dụng lên một đơn vị chiều dài của dây là?
Ta có: \(F = {2.10^{ - 7}}\frac{{{I_1}{I_2}}}{r} = {2.10^{ - 7}}\frac{{2.5}}{{0,1}} = {2.10^{ - 5}}N\)
Hai vòng tròn dây dẫn đặt cách nhau một khoảng rất nhỏ. Vòng dây dẫn được giữ cố định. Vòng trên được nối với một đòn cân. Khi có 2 dòng điện có cường độ bằng nhau vào 2 dây dẫn thì chúng hút nhau. Đặt thêm một quả cân khối lượng \(0,1g\) vào đĩa cân bên kia thì cân trở lại thăng bằng và lúc đó hai vòng dây cách nhau 2mm. Xác định cường độ dòng điện trong mỗi vòng dây. Biết bán kính mỗi vòng dây là \(5cm\). Lấy \(g = 10m/s^2\)

Cân nằm thăng bằng khi: \(F = P = mg\) (1)
Ta có, lực từ tác dụng lên mỗi đơn vị chiều dài của vòng dây:
\({F_0} = \dfrac{F}{{2\pi R}} = {2.10^{ - 7}}\dfrac{{{I_1}{I_2}}}{r} = {2.10^{ - 7}}\dfrac{{{I^2}}}{r}{\rm{ (2)}}\)
Từ (1) và (2), ta có: \({2.10^{ - 7}}\dfrac{{{I^2}}}{r} = \dfrac{{mg}}{{2\pi R}} \\\to I = \sqrt {\dfrac{{mg{\rm{r}}}}{{4\pi {{.10}^{ - 7}}.R}}} = \sqrt {\dfrac{{0,{{1.10}^{ - 3}}{\rm{.10}}{\rm{.2}}{\rm{.1}}{{\rm{0}}^{ - 3}}}}{{4\pi {{.10}^{ - 7}}{{.5.10}^{ - 2}}}}} = 5,64A\)

