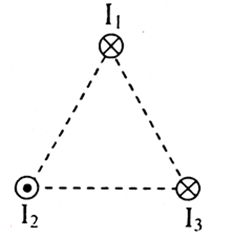
Ba dây dẫn thẳng dài song song cách đều nhau một khoảng \(a = 10cm\) như hình vẽ. Cường độ dòng điện \({I_1} = 25A\), \({I_2} = {I_3} = 10A\). Xác độ lớn của lực từ tác dụng lên \(1m\) của dây \({I_1}\)?
Trả lời bởi giáo viên
Ta có, lực do các dòng \({I_2},{I_3}\) tác dụng lên \({I_1}\)
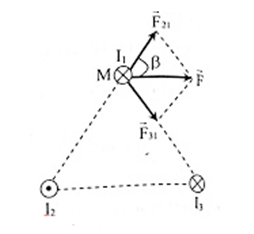
Ta có:
\({r_{21}} = {r_{31}} = a = 10cm = 0,1m\)
\({I_2} = {I_3} = 10A\)
\({F_{21}} = {2.10^{ - 7}}\dfrac{{{I_2}{I_1}}}{{{r_{21}}}}.l = {2.10^{ - 7}}.\dfrac{{10.25}}{{0,1}} = {5.10^{ - 4}}N\)
\({F_{31}} = {2.10^{ - 7}}\dfrac{{{I_3}{I_1}}}{{{r_{31}}}}l = {2.10^{ - 7}}\dfrac{{10.25}}{{0,1}}.1 = {5.10^{ - 4}}N = {F_{21}}\)
Lực tổng hợp do các dòng \({I_2},{I_3}\) tác dụng lên \({I_1}\): \(\overrightarrow F = \overrightarrow {{F_{21}}} + \overrightarrow {{F_{31}}} \)
Do \(\Delta {I_1}{I_2}{I_3}\) là tam giác đều \( \Rightarrow \widehat {{I_3}{I_1}{I_2}} = {60^0} = \beta \)
Từ hình, ta có: \(F = 2{F_{21}}cos\beta = {2.5.10^{ - 4}}.cos{60^0} = {5.10^{ - 4}}N\)
Hướng dẫn giải:
+ Vận dụng biểu thức xác định lực từ tác dụng lên đoạn dây dài \(l\) : \(F = {2.10^{ - 7}}\dfrac{{{I_1}{I_2}}}{r}l\)
+ Vận dụng quy tắc tổng hợp lực

