Câu hỏi:
2 năm trước
Hai vòng tròn dây dẫn đặt cách nhau một khoảng rất nhỏ. Vòng dây dẫn được giữ cố định. Vòng trên được nối với một đòn cân. Khi có 2 dòng điện có cường độ bằng nhau vào 2 dây dẫn thì chúng hút nhau. Đặt thêm một quả cân khối lượng \(0,2g\) vào đĩa cân bên kia thì cân trở lại thăng bằng và lúc đó hai vòng dây cách nhau \(1mm\). Xác định cường độ dòng điện trong mỗi vòng dây. Biết bán kính mỗi vòng dây là \(4cm\). Lấy \(g{\rm{ }} = {\rm{ }}10m/{s^2}\) .
Trả lời bởi giáo viên
Đáp án đúng: b
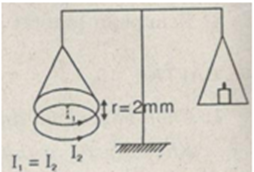
Cân nằm thăng bằng khi: F = P = mg (1)
Ta có, lực từ tác dụng lên mỗi đơn vị chiều dài của vòng dây:
\({F_0} = \dfrac{F}{{2\pi R}} = {2.10^{ - 7}}\dfrac{{{I_1}{I_2}}}{r} = {2.10^{ - 7}}\dfrac{{{I^2}}}{r}{\rm{ (2)}}\)
Từ (1) và (2), ta có:
\(\begin{array}{l}{2.10^{ - 7}}\dfrac{{{I^2}}}{r} = \dfrac{{mg}}{{2\pi R}}\\ \to I = \sqrt {\dfrac{{mg{\rm{r}}}}{{4\pi {{.10}^{ - 7}}.R}}} = \sqrt {\dfrac{{0,{{2.10}^{ - 3}}{\rm{.10}}{\rm{.1}}{\rm{.1}}{{\rm{0}}^{ - 3}}}}{{4\pi {{.10}^{ - 7}}{{.4.10}^{ - 2}}}}} = 6,31A\end{array}\)
Hướng dẫn giải:
+ Sử dụng điều kiện cân bằng của vật
+ Vận dụng biểu thức xác định lực từ tác dụng lên mỗi đơn vị chiều dài dây: \(F = {2.10^{ - 7}}\dfrac{{{I_1}{I_2}}}{r}\)
Câu hỏi khác
- Bài tập từ trường của dòng điện trong các dây dẫn có hình dạng đặc biệt có lời giải MÔN LÝ lớp 11
- Bài tập lực từ - bài tập lực từ tác dụng lên đoạn dây dẫn mang điện lý 11 có lời giải
- Bài tập tương tác giữa hai dòng điện song song lý 11 có lời giải
- Bài tập khung dây đặt trong từ trường đều lý 11 có lời giải
- Bài tập từ trường lý 11 có lời giải
