Cho hệ 3 dòng điện đặt song song như hình:
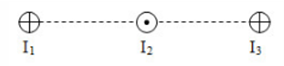
\({I_1} = 10A,{\rm{ }}{I_2} = {I_3} = 20A,{\rm{ }}{r_{12}} = {\rm{ }}{r_{23}} = 4cm\). Lực từ tác dụng lên 1m chiều dài của I1 có giá trị là:
- Xác định lực từ do dòng I2, I3 tác dụng lên I1 ta có:
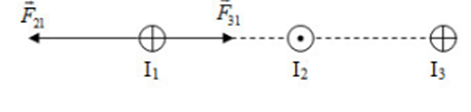
Ta có:
+ \({F_{21}} = {2.10^{ - 7}}\frac{{{I_1}{I_2}}}{{{r_{21}}}} = {2.10^{ - 7}}\frac{{10.20}}{{0,04}} = {10^{ - 3}}A\)
+ \({F_{31}} = {2.10^{ - 7}}\frac{{{I_3}{I_1}}}{{{r_{31}}}} = {2.10^{ - 7}}\frac{{10.20}}{{0,04 + 0,04}} = {5.10^{ - 4}}A\)
Lực từ tác dụng lên 1m chiều dài của I1 có giá trị là:
\(F = {F_{21}} - {F_{31}} = {10^{ - 3}} - {5.10^{ - 4}} = {5.10^{ - 4}}N\)
Cho hệ 3 dòng điện song song như hình vẽ:
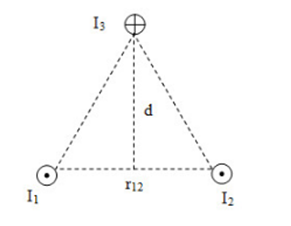
Biết \({I_1} = {I_2} = 20A,{\rm{ }}{I_3} = 10A,{r_{12}} = 20cm\), I3 nằm trong mặt phẳng trung trực của I1 và I2 cách mặt phẳng chứa I1; I2 một khoảng là d. Lực tác dụng lên 1m chiều dài của I3 nếu d = 10cm có độ lớn bằng:
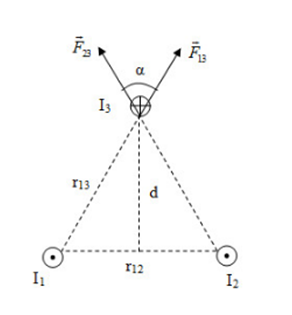
Ta có:
+ \({r_{13}} = {r_{23}} = \sqrt {{d^2} + {{\left( {\frac{{{r_{12}}}}{2}} \right)}^2}} = \sqrt {{{10}^2} + {{\left( {\frac{{20}}{2}} \right)}^2}} = 10\sqrt 2 cm\)
+ \({F_{13}} = {F_{23}} = {2.10^{ - 7}}\frac{{{I_1}{I_3}}}{{{r_{13}}}} = {2.10^{ - 7}}\frac{{20.10}}{{0,1\sqrt 2 }} = 2\sqrt 2 {.10^{ - 4}}N\)
+ \(r_{12}^2 = r_{13}^2 + r_{23}^2 - 2{{\rm{r}}_{13}}{r_{23}}{\rm{cos}}\alpha \to {\rm{cos}}\alpha = \frac{{r_{13}^2 + r_{23}^2 - r_{12}^2}}{{2{{\rm{r}}_{13}}{r_{23}}}} = 0\)
\( \to {F_{13}} \bot {F_{23}} \to {F_3} = \sqrt {F_{13}^2 + F_{23}^2} = {F_{13}}\sqrt 2 = \sqrt 2 .2\sqrt 2 {.10^{ - 4}} = {4.10^{ - 4}}N\)
Hai dây dẫn thẳng dài song song được đặt trong không khí, cường độ dòng điện trong hai dây dẫn bằng nhau và bằng I = 1A. Lực từ tác dụng lên mỗi đơn vị chiều dài của dây bằng 2.10-5N. Khoảng cách giữa hai dây khi đó là:
Ta có: Lực từ tác dụng lên mỗi đơn vị chiều dài dây: \(F = {2.10^{ - 7}}\frac{{{I^2}}}{r} \to r = {2.10^{ - 7}}\frac{{{I^2}}}{F} = {2.10^{ - 7}}\frac{{{1^2}}}{{{{2.10}^{ - 5}}}} = 0,01m = 1cm\)
Dây dẫn thẳng dài có \({I_1} = 15A\) đi qua đặt trong không khí. Lực từ tác dụng lên 1m dây của dòng I2 = 10A đặt song song cách I1 đoạn 15cm là lực hút hay đẩy và có giá trị bằng bao nhiêu? Biết I1 và I2 ngược chiều nhau.
Ta có, 2 dòng I1 và I2 ngược chiều nhau => lực tương tác là lực đẩy \(F = {2.10^{ - 7}}\frac{{{I_1}{I_2}}}{r} = {2.10^{ - 7}}\frac{{15.10}}{{0,15}} = {2.10^{ - 4}}N\)
Hai dây thẳng dài vô hạn đặt cách nhau 4cm, 2 dòng điện có chiều như hình vẽ, 2 dòng điện có cùng cường độ I = 5A.


Ta có: 2 dòng ngược chiều nhau => lực tương tác là lực đẩy
\(F = {2.10^{ - 7}}\frac{{{I_1}{I_2}}}{r} = {2.10^{ - 7}}\frac{{{5^2}}}{{0,04}} = 1,{25.10^{ - 4}}N\)
Ba dây dẫn thẳng dài được đặt song song trong cùng mặt phẳng thẳng đứng như hình vẽ. Dây 1 và dây 3 được giữ cố định có dòng điện chạy xuống và I1 > I3 . Xác định chiều của dòng I2 nếu dây 2 bị dịch sang phải?
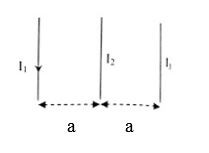
Ta có:
\({F_{12}} = {2.10^{ - 7}}\dfrac{{{I_1}{I_2}}}{a}\)
\({F_{32}} = {2.10^{ - 7}}\dfrac{{{I_3}{I_2}}}{a}\)
Theo đầu bài ta có: \({I_1} > {I_3} \to {F_{12}} > {F_{23}}\)
Muốn dây 2 dịch sang phải thì F12 phải hướng sang phải
=> F12 là lực đẩy => I1 và I2 ngược chiều nhau
=> I2 hướng lên
Hai dòng điện vô hạn đặt song song cách nhau 30cm mang hai dòng điện cùng chiều \({I_1} = 20A;{I_2} = 40A\) . Cần đặt dòng I3 cách I1, I2 một khoảng bao nhiêu để lực từ tác dụng lên I3 bằng 0?
Ta có:
\(\overrightarrow {{F_3}} = \overrightarrow {{F_{13}}} + \overrightarrow {{F_{23}}} = 0 \to \overrightarrow {{F_{13}}} = - \overrightarrow {{F_{23}}} \)
=> I1, I2 cùng chiều và \({F_{13}} = {F_{23}}\)
=> I3 phải nằm giữa I1 và I2
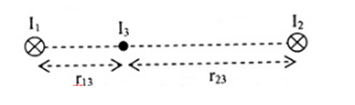
+ \({F_{13}} = {F_{23}} \to \frac{{{I_1}}}{{{r_{13}}}} = \frac{{{I_2}}}{{{r_{23}}}} \to {r_{13}} = 0,5{{\rm{r}}_{23}}\)
Mặt khác, ta có: \({r_{13}} + {r_{23}} = 30cm\)
\( \to \left\{ \begin{array}{l}{r_{13}} = 10cm\\{r_{23}} = 20cm\end{array} \right.\)
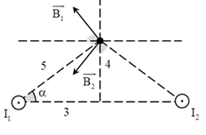
Ba dây dẫn thẳng dài đặt cách đều nhau khoảng a = 10cm như hình vẽ. Cường độ dòng điện chạy trong 3 dây lần lượt là I1 = 25A, I2 = I3 = 10A. Độ lớn của lực từ tác dụng lên 1m của dây I1 là
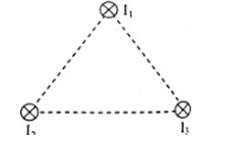
Ta có:
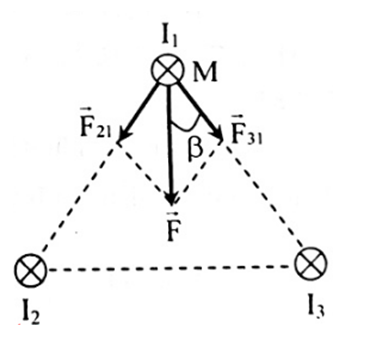
\(\begin{array}{l}{F_{21}} = {F_{31}} = {2.10^{ - 7}}\frac{{{I_1}{I_2}}}{{{r_{21}}}} = {5.10^{ - 4}}N\\F = 2{F_{21}}{\rm{cos3}}{{\rm{0}}^0} = 5\sqrt 3 {.10^{ - 4}}N\end{array}\)
Hai dòng điện thẳng đặt song song cách nhau 40cm mang hai dòng điện cùng chiều \({I_1} = {I_2} = 10A\). Dòng thứ 3 đặt song song với hai dòng điện trên và thuộc mặt phẳng trung trực của 2 dòng I1 và I2. Biết \({I_3} = 10A\), ngược chiều với I1 và I3 cách mặt phẳng chứa (I1, I2) đoạn d = 20cm. Lực từ tác dụng lên 1m của dòng I3.
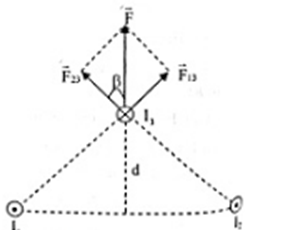
\(\begin{array}{l}{r_{13}} = {r_{23}} = \sqrt {{d^2} + \frac{{r_{12}^2}}{4}} = 0,2\sqrt 2 m\\{I_1} = {I_2} \to {F_{13}} = {F_{23}} = {2.10^{ - 7}}\frac{{{I_1}{I_3}}}{{{r_{13}}}} = \frac{1}{{\sqrt 2 }}{.10^{ - 4}}N\\{\rm{cos}}\beta {\rm{ = }}\frac{d}{{{r_{23}}}} = \frac{1}{{\sqrt 2 }} \to \beta = {45^0}\\ \to F = 2{F_{23}}{\rm{cos4}}{{\rm{5}}^0} = {10^{ - 4}}N\end{array}\)
Hai dòng điện thẳng đặt song song cách nhau \(40cm\) mang hai dòng điện cùng chiều \({I_1} = {I_2} = 10A\). Dòng thứ 3 đặt song song với hai dòng điện trên và thuộc mặt phẳng trung trực của 2 dòng I1 và I2. Biết \({I_3} = 10A\), ngược chiều với I1 và I3 cách mặt phẳng chứa (I1, I2) đoạn d . d = ? để lực từ tác dụng lên 1m của dòng I3 đạt giá trị cực đại?
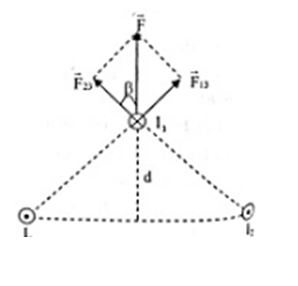
\(\begin{array}{l}{r_{13}} = {r_{23}} = \sqrt {{d^2} + \dfrac{{r_{12}^2}}{4}} \\{I_1} = {I_2} \to {F_{13}} = {F_{23}} = {2.10^{ - 7}}\dfrac{{{I_1}{I_3}}}{{{r_{13}}}} = {2.10^{ - 5}}\dfrac{1}{{\sqrt {{d^2} + 0,04} }}\\{\rm{cos}}\beta {\rm{ = }}\dfrac{d}{{{r_{23}}}} = \dfrac{d}{{\sqrt {{d^2} + 0,04} }}\\ \to F = 2{F_{23}}{\rm{cos}}\beta = {2.2.10^{ - 5}}\dfrac{1}{{\sqrt {{d^2} + 0,04} }}.\dfrac{d}{{\sqrt {{d^2} + 0,04} }} = \dfrac{{{{4.10}^{ - 5}}d}}{{{d^2} + 0,04}} = \dfrac{{{{4.10}^{ - 5}}}}{{d + \dfrac{{0,04}}{d}}}\end{array}\)
Ta có: Fmax khi: \({\left[ {d + \dfrac{{0,{2^2}}}{d}} \right]_{{\rm{min}}}}\)
Xét: \(d + \dfrac{{0,04}}{d} \ge 2\sqrt {d.\dfrac{{0,04}}{d}} = 0,4\)
Dấu “ = ” xảy ra khi: \(d = \dfrac{{0,04}}{d} \to d = 0,2m\)
Cho hai dòng điện I1 = I2 = 6A chạy trong hai dây dẫn dài, song song, cách nhau 30cm theo cùng một chiều (hình vẽ). Xác định cảm ứng từ tổng hợp tại điểm M nằm trong mặt phẳng chứa hai dây dẫn, cách hai dây lần lượt MO1 = 10cm, MO2 = 20cm.

Biểu diễn vec tơ cảm ứng từ tổng hợp tại M do hai dòng điện gây ra như hình vẽ.
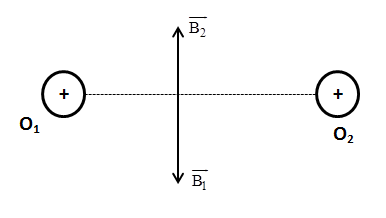
Ta có: \(\overrightarrow{{{B}_{M}}}=\overrightarrow{{{B}_{1}}}+\overrightarrow{{{B}_{2}}}\)
Vì \(\overrightarrow{{{B}_{1}}},\overrightarrow{{{B}_{2}}}\) song song và ngược chiều nhau nên
BM = |B1 – B2|
Mà \({{B}_{1}}={{2.10}^{-7}}\frac{{{I}_{1}}}{M{{O}_{1}}}={{12.10}^{-6}}T;{{B}_{2}}={{2.10}^{-7}}\frac{{{I}_{2}}}{M{{O}_{2}}}={{6.10}^{-6}}T\)
Nên BM = 6.10-6T
Hai dây dẫn thẳng, dài song song cách nhau 32 cm trong không khí, dòng điện chạy trên dây 1 là I1 = 5 A, dòng điện chạy trên dây 2 là I2 = 1 A và ngược chiều với I1. Điểm M nằm trong mặt phẳng của hai dây và cách đều hai dây. Cảm ứng từ tại M có độ lớn là:
Cảm ứng từ do I1 và I2 gây ra tại M là
\({B_1} = {2.10^{ - 7}}.{{{I_1}} \over {r_1^2}} = {2.10^{ - 7}}.{5 \over {0,16}} = 6,{25.10^{ - 6}}T;{B_2} = {2.10^{ - 7}}.{{{I_2}} \over {r_2^2}} = {2.10^{ - 7}}.{1 \over {0,16}} = 1,{25.10^{ - 6}}T\)
Cảm ứng từ tổng hợp tại M là \(\overrightarrow {{B_M}} = \overrightarrow {{B_1}} + \overrightarrow {{B_2}} \)
Ta có hình vẽ sau
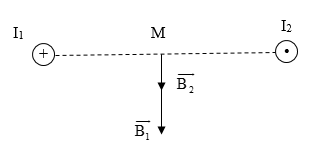
Từ hình vẽ ta thấy BM = B1 + B2 = 7,5.10-6 T.
Hai dây dẫn thẳng dài đặt song song, cách nhau 6 cm trong không khí. Trong hai dây dẫn có hai dòng điện cùng chiều có cùng cường độ I1 = I2 =2 A. Cảm ứng từ tại điểm M cách mỗi dây 5 cm là
+ Hai dây dẫn cách nhau 6 cm, điểm M cách mỗi dây 5 cm M nằm trên trung trực của \({I_1}{I_2}\) và cách trung điểm O của \({I_1}{I_2}\) một đoạn 4 cm.
+ Cảm ứng từ do các dòng điện gây ra tại I có độ lớn \(B = {2.10^{ - 7}}{I \over r} = {8.10^{ - 6}}\,\,T.\)
+ Chiều được xác định theo quy tắc nắm tay phải.
Từ hình vẽ ta có \({B_M} = 2B\sin \alpha = {2.8.10^{ - 6}}{4 \over 5} = 12,{8.10^{ - 6}}\,\,T.\)
Hai dòng điện cùng chiều cường độ \({I_1} = {I_2} = 10\,\,A\) chạy trong hai dây dẫn thẳng song song dài vô hạn, được đặt trong chân không cách nhau một khoảng \(a = 10\,\,cm\). Một điểm \(M\) cách đều hai dòng điện một khoảng \(x\). Để cảm ứng từ tổng hợp tại \(M\) đạt giá trị lớn nhất thì \(x\) có giá trị là bao nhiêu? Giá trị cảm ứng từ cực đại \({B_{max}}\) khi đó là bao nhiêu?
Ta có hình vẽ:
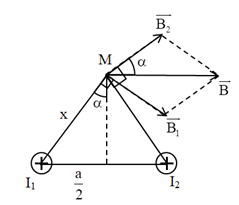
Cảm ứng từ do mỗi dòng điện gây ra là: \({B_1} = {B_2} = {2.10^{ - 7}}\frac{I}{x}\)
Từ hình vẽ ta thấy: \(B = 2{B_1}\cos \alpha \)
Lại có: \(\cos \alpha = \frac{{\sqrt {{x^2} - {{\left( {\frac{a}{2}} \right)}^2}} }}{x} = \frac{{\sqrt {{x^2} - \frac{{{a^2}}}{4}} }}{x}\)\( \Rightarrow B = {2.2.10^{ - 7}}I.\frac{{\sqrt {{x^2} - \frac{{{a^2}}}{4}} }}{{{x^2}}}\)
Xét hàm số: \(y = \frac{{\sqrt {{x^2} - \frac{{{a^2}}}{4}} }}{{{x^2}}} = \sqrt {\frac{1}{{{x^2}}} - \frac{{{a^2}}}{{4{x^4}}}} \)
Ta có: \({y^2} = \frac{1}{{{x^2}}} - \frac{{{a^2}}}{{4{x^4}}} = - {\left( {\frac{a}{2}} \right)^2}.{\left( {\frac{1}{{{x^2}}}} \right)^2} + 2.\frac{a}{2}.\frac{1}{a}.\frac{1}{{{x^2}}} - {\left( {\frac{1}{a}} \right)^2} + {\left( {\frac{1}{a}} \right)^2}\)
\( \Rightarrow {y^2} = - {\left( {\frac{a}{2}.\frac{1}{{{x^2}}} - \frac{1}{a}} \right)^2} + \frac{1}{{{a^2}}}\)
Mà \({\left( {\frac{a}{2}.\frac{1}{{{x^2}}} - \frac{1}{a}} \right)^2} \ge 0 \Rightarrow - {\left( {\frac{a}{2}.\frac{1}{{{x^2}}} - \frac{1}{a}} \right)^2} + \frac{1}{{{a^2}}} \le \frac{1}{{{a^2}}}\)
\( \Rightarrow {\left( {{y^2}} \right)_{\max }} = \frac{1}{{{a^2}}} \Rightarrow {y_{\max }} = \frac{1}{a}\)
Khi \(\frac{a}{2}.\frac{1}{{{x^2}}} - \frac{1}{a} = 0 \Rightarrow \frac{1}{{{x^2}}} = \frac{2}{{{a^2}}} \Rightarrow x = \frac{a}{{\sqrt 2 }} = 5\sqrt 2 \,\,\left( {cm} \right)\)
\( \Rightarrow {B_{\max }} = {2.2.10^{ - 7}}I.{y_{\max }} = {2.2.10^{ - 7}}.I.\sqrt {\frac{1}{{{a^2}}}} = {4.10^{ - 5}}\,\,\left( T \right)\)
Hai dây dẫn thẳng dài, song song và cách nhau \(10\,\,cm\) trong chân không, dòng điện trong hai dây cùng chiều có cường độ \({I_1} = 2\,\,A\) và \({I_2} = 5\,\,A\). Lực từ tác dụng lên \(20\,\,cm\) chiều dài của mỗi dây là
Hai dòng điện cùng chiều, lực tương tác giữa hai dây dẫn là lực hút
Lực tương tác giữa hai dây dẫn là:
\(F = {2.10^{ - 7}}.\dfrac{{{I_1}{I_2}}}{d}.{\rm{l}} = {2.10^{ - 7}}.\dfrac{{2.5}}{{0,1}}.0,2 = {4.10^{ - 6}}\,\,\left( N \right)\)

