Câu hỏi:
2 năm trước
Hai dòng điện thẳng đặt song song cách nhau \(40cm\) mang hai dòng điện cùng chiều \({I_1} = {I_2} = 10A\). Dòng thứ 3 đặt song song với hai dòng điện trên và thuộc mặt phẳng trung trực của 2 dòng I1 và I2. Biết \({I_3} = 10A\), ngược chiều với I1 và I3 cách mặt phẳng chứa (I1, I2) đoạn d . d = ? để lực từ tác dụng lên 1m của dòng I3 đạt giá trị cực đại?
Trả lời bởi giáo viên
Đáp án đúng: d
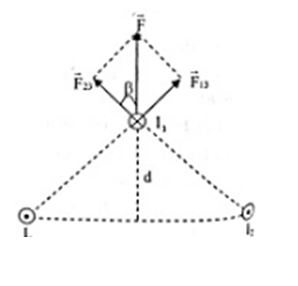
\(\begin{array}{l}{r_{13}} = {r_{23}} = \sqrt {{d^2} + \dfrac{{r_{12}^2}}{4}} \\{I_1} = {I_2} \to {F_{13}} = {F_{23}} = {2.10^{ - 7}}\dfrac{{{I_1}{I_3}}}{{{r_{13}}}} = {2.10^{ - 5}}\dfrac{1}{{\sqrt {{d^2} + 0,04} }}\\{\rm{cos}}\beta {\rm{ = }}\dfrac{d}{{{r_{23}}}} = \dfrac{d}{{\sqrt {{d^2} + 0,04} }}\\ \to F = 2{F_{23}}{\rm{cos}}\beta = {2.2.10^{ - 5}}\dfrac{1}{{\sqrt {{d^2} + 0,04} }}.\dfrac{d}{{\sqrt {{d^2} + 0,04} }} = \dfrac{{{{4.10}^{ - 5}}d}}{{{d^2} + 0,04}} = \dfrac{{{{4.10}^{ - 5}}}}{{d + \dfrac{{0,04}}{d}}}\end{array}\)
Ta có: Fmax khi: \({\left[ {d + \dfrac{{0,{2^2}}}{d}} \right]_{{\rm{min}}}}\)
Xét: \(d + \dfrac{{0,04}}{d} \ge 2\sqrt {d.\dfrac{{0,04}}{d}} = 0,4\)
Dấu “ = ” xảy ra khi: \(d = \dfrac{{0,04}}{d} \to d = 0,2m\)
Hướng dẫn giải:
+ Vận dụng quy tắc tổng hợp lực
+ Vận dụng biểu thức xác định lực từ tác dụng lên mỗi đơn vị chiều dài dây: \(F = {2.10^{ - 7}}\dfrac{{{I_1}{I_2}}}{r}\)
Câu hỏi khác
- Bài tập từ trường của dòng điện trong các dây dẫn có hình dạng đặc biệt có lời giải MÔN LÝ lớp 11
- Bài tập lực từ - bài tập lực từ tác dụng lên đoạn dây dẫn mang điện lý 11 có lời giải
- Bài tập tương tác giữa hai dòng điện song song lý 11 có lời giải
- Bài tập khung dây đặt trong từ trường đều lý 11 có lời giải
- Bài tập từ trường lý 11 có lời giải
