Cho mạch điện có sơ đồ như hình vẽ, trong đó : E1 = 8V; r1 = 1,2Ω; E2 = 4 V; r2 = 0,4Ω, R = 28,4Ω; hiệu điện thế giữa hai đầu đoạn mạch đo được là UAB = 6V.
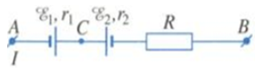
Cho biết mạch điện này chứa nguồn điện nào và chứa máy thu nào?
Cách giải:
Giả sử dòng điện mạch có chiều từ A đến B. Hiệu điện thế giữa hai đầu A và B là:
\({U_{AB}} = - {E_1} + {E_2} + I\left( {R + {r_1} + {r_2}} \right) \Rightarrow I = \frac{{{U_{AB}} + {E_1} - {E_2}}}{{R + {r_1} + {r_2}}} = \frac{{6 + 8 - 4}}{{28,4 + 1,2 + 0,4}} = \frac{1}{3}A\)
Vì I > 0 nên chiều dòng điện đã chọn từ A đến B là chiều đúng
Dòng điện trong mạch theo chiều từ A đến B nên:
+ Với E1: dòng điện đi từ cực âm đến cực dương nên E1 đóng vai trò nguồn điện.
+ Với E2: dòng điện đi từ cực dương đến cực âm nên E2 đóng vai trò máy thu.
Hai nguồn điện có suất điện động E, điện trở mỗi nguồn là r1, r2, mắc nối tiếp với một điện trở R như hình vẽ. Số chỉ của Vôn kế là 0V. Giá trị của điện trở R là
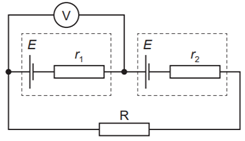
Cường độ dòng điện trong mạch là: \(I = \dfrac{{2E}}{{R + {r_1} + {r_2}}}\)
Số chỉ của Vôn kế là: \({U_V} = E - I.{r_1} = 0\)
\( \Rightarrow E - \dfrac{{2E.{r_1}}}{{R + {r_1} + {r_2}}} = 0 \Rightarrow {r_1} = R + {r_2} \Rightarrow R = {r_1} - {r_2}\)
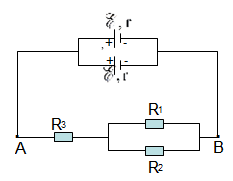
Hai pin được ghép với nhau theo các sơ đồ ở hình vẽ. Tìm cường độ dòng điện trong mạch và hiệu điện thế giữa hai điểm A, B. Biết hai pin ghép xung đối có suất điện động và điện trở tương ứng là E1, r1 và E2, r2 (E1 > E2)
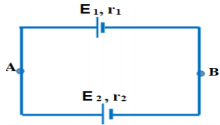
Cách giải:
Chọn chiều dòng điện như hình vẽ.
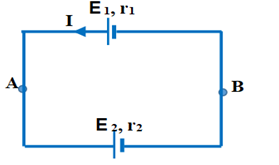
Áp dụng định luật Ôm cho đoạn mạch AB ta có: \(\left\{ \begin{array}{l}{U_{AB}} = {E_1} - I.{r_1}\\{U_{AB}} = {E_2} + I.{r_2}\end{array} \right. \Rightarrow I = \frac{{{E_1} - {E_2}}}{{{r_1} + {r_2}}}\,\)
Áp dụng định luật Ôm cho đoạn mạch chứa E2:
\({U_{AB}} = {E_2} + I.{r_2} = {E_2} + \frac{{{E_1} - {E_2}}}{{{r_1} + {r_2}}}.{r_2} = \frac{{{E_2}{r_1} + {E_1}{r_2}}}{{{r_1} + {r_2}}}\)
Cho mạch điện như hình bên. Biết \(E = 12 V\); \(r = 1 Ω\); \(R_1= 5 Ω\); \(R_2=R_3= 10 Ω\). Bỏ qua điện trở của dây nối. Hiệu điện thế giữa hai đầu \(R_1\) là:
Hiệu điện thế giữa hai đầu R1 là \(U = \xi - \dfrac{{\xi .r}}{{r + \dfrac{{{R_1}\left( {{R_2} + {R_3}} \right)}}{{{R_1} + {R_2} + {R_3}}}}} = 12 - \dfrac{{12.1}}{{1 + \dfrac{{5(10 + 10)}}{{5 + 10 + 10}}}} = 9,6V\)
Người ta mắc hai cực của nguồn điện với một biến trở có thể thay đổi giá trị từ \(0\) đến vô cùng. Khi giá trị của biến trở rất lớn thì hiệu điện thế giữa hai cực của nguồn điện là \(4,5 V\). Giảm giá trị của biến trở đến khi cường độ dòng điện trong mạch là \(2 A\) thì hiệu điện thế giữa hai cực của nguồn điện là \(4 V\). Suất điện động và điện trở trong của nguồn điện lần lượt là
+ E = U1 + \(\underbrace {{I_1}}_{ = \dfrac{E}{{{R_\infty } + r}} = 0}.r = {U_1} = \)\(4,5(V)\);
+ \(E = \underbrace {{U_2}}_{4(V)} + \underbrace {{I_2}}_{2(A)}.r = 4,5(V) \to r = \)\(0,25(\Omega )\)
Một bộ nguồn gồm n nguồn điện giống nhau. Mỗi nguồn có suất điện động \(\xi \) và điện trong r. Các nguồn này ghép song song nhau. Điện trở trong của bộ nguồn được xác định bởi biểu thức:
Bộ n nguồn mắc song song có: \(\left\{ \begin{array}{l}{\xi _b} = \xi \\{r_b} = \dfrac{r}{n}\end{array} \right.\)
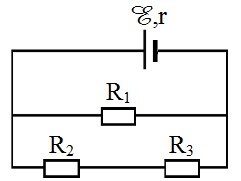
Cho mạch điện như hình vẽ. E =12 V ; r = 4Ω ; R1 =12Ω; R2 =24Ω ; R3= 8Ω. Cường độ dòng điện trong toàn mạch là:
Ta có: \({R_3}nt\left( {{R_1}//{R_2}} \right)\)
\({R_{12}} = \dfrac{{{R_1}.{R_2}}}{{{R_1} + {R_2}}} = \dfrac{{12.24}}{{12 + 24}} = 8\Omega \)
\({R_N} = {R_{12}} + {R_3} = 8 + 8 = 16\Omega \)
Cường độ dòng điện trong toàn mạch là:
\(I = \dfrac{E}{{{R_N} + r}} = \dfrac{{12}}{{16 + 4}} = 0,6{\rm{A}}\)
Có một số điện trở có \(r = 3\,\,\Omega \). Số điện trở \(r\) tối thiểu phải dùng để mắc thành mạch có điện trở \(5\,\,\left( \Omega \right)\) là:
Do \({R_{td}} > r \to \) có ít nhất 1 điện trở \(r\) mắc nối tiếp với \({R_x}\)
Ta có: \({R_{td}} = r + {R_x} \Rightarrow {R_x} = {R_{td}} - r = 5 - 3 = 2\,\,\left( \Omega \right)\)
Ta thấy \({R_x} < r \to \) có ít nhất 1 điện trở \(r\) mắc song song với \({R_y}\)
Ta có: \(\frac{1}{{{R_x}}} = \frac{1}{r} + \frac{1}{{{R_y}}} \Rightarrow \frac{1}{2} = \frac{1}{3} + \frac{1}{{{R_y}}} \Rightarrow {R_y} = 6\,\,\left( \Omega \right)\)
Ta thấy \({R_y} = 6\Omega = 2r \to \) đoạn mạch \({R_y}\) gồm \(2\) điện trở \(r\) mắc nối tiếp
Ta có sơ đồ mạch điện:
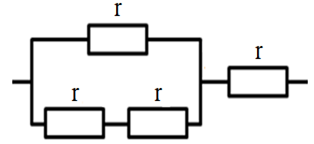
Vậy cần ít nhất \(4\) điện trở
Cho 3 pin giống nhau, mỗi pin có suất điện động 3V. Ghép 3 pin nối tiếp với nhau thì suất điện động của bộ pin là
Suất điện động của bộ pin là:
ξ = nξ0 = 3.3 = 9 (V)
Một nguồn điện có suất điện động 5 V và điện trở trong 1 Ω được mắc với điện trở ngoài 3 Ω thành mạch kín. Cường độ dòng điện chạy trong mạch là
Cường độ dòng điện trong mạch là:
\(I = \dfrac{E}{{r + R}} = \dfrac{5}{{1 + 3}} = 1,25\,\,\left( A \right)\)
Cho mạch điện như hình bên. Biết \(E = 12V;\,\,r = 1\Omega ;\,\,{R_1} = 5\Omega ;\,\,\,{R_2} = {R_3} = 10\Omega .\) Bỏ qua điện trở của dây nối. Hiệu điện thế giữa hai đầu \({R_1}\) là
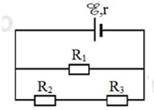
Điện trở tương đương của mạch ngoài là:
\(R = \dfrac{{{R_1}.\left( {{R_2} + {R_3}} \right)}}{{{R_1} + \left( {{R_2} + {R_3}} \right)}} = \dfrac{{5.\left( {10 + 10} \right)}}{{5 + \left( {10 + 10} \right)}} = 4\,\,\left( \Omega \right)\)
Cường độ dòng điện mạch chính là:
\(I = \dfrac{E}{{R + r}} = \dfrac{{12}}{{4 + 1}} = 2,4\,\,\left( A \right)\)
Do \({R_1}//{R_{23}} \Rightarrow {U_1} = {U_{23}} = U\)
Ta có: \(U = E - I.r = 12 - 2,4.1 = 9,6\,\,\left( V \right)\)
Cho mạch điện như hình vẽ, bỏ qua điện trở của dây nối, biết \(E = 3 V\),\({R_1} = 5\Omega \) ampe kế chỉ \(0,3 A\), vôn kế chỉ \(1,2 V\). Ampe kế và vôn kế lí tưởng. Giá trị điện trở trong \(r\) của nguồn là
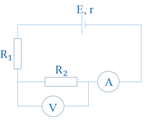
Từ biểu thức: \(E = I\left( {r + {R_1} + {R_2}} \right) \Rightarrow E = I.(r + {R_1}) + {U_2} \Leftrightarrow 3 = 0,3.(r + 5) + 1,2\)
\( \Rightarrow r = 1(\Omega )\)
Công thức nào là định luật Ôm cho mạch điện kín gồm một nguồn điện và một điện trở ngoài:
Biểu thức định luật Ôm cho đoạn mạch kín gồm một nguồn điện và một điện trở ngoài là:
\(I = \frac{E}{{R + r}}\)
Cho mạch điện như hình vẽ. Biểu thức nào sau đây đúng:
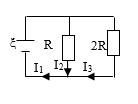
Ta có:
+ Tổng trở mạch ngoài:
\({R_{ng}} = \dfrac{{R.2R}}{{R + 2{\rm{R}}}} = \dfrac{2}{3}R\)
+ \(I = \dfrac{E}{{\dfrac{2}{3}R + r}}\)
+ \({U_2} = {U_3} \leftrightarrow {I_2}.R = {I_3}.2R \leftrightarrow {I_2} = 2{I_3}\)
+ I = I2 + I3
Việc ghép nối tiếp các nguồn điện để
Suất điện động bộ nguồn khi ghép nối tiếp: Eb = E1 + E2 + E3 +…. + En
=> Việc ghép nối tiếp các nguồn sẽ có được bộ nguồn có suất điện động lớn hơn các nguồn có sẵn
Việc ghép song song các nguồn điện giống nhau thì
Khi mắc song song các nguồn điện giống nhau, ta có:
- Suất điện động bộ nguồn: Eb = E.
- Điện trở trong bộ nguồn: rb = \(\frac{r}{n}\).
Trong một mạch điện kín nếu mạch ngoài thuần điện trở RN thì hiệu suất của nguồn điện có điện trở r được tính bởi biểu thức:
Mạch ngoài thuần điện trở RN thì hiệu suất của nguồn điện có điện trở r được tính bởi biểu thức:
\(H = \;\frac{{{R_N}}}{{{R_N} + r}}.100\% \)
Một nguồn điện với suất điện động E, điện trở trong r, mắc với một điện trở ngoài R = r thì cường độ dòng điện chạy trong mạch là I. Nếu thay nguồn điện đó bằng 3 nguồn điện giống hệt nó mắc song song thì cường độ dòng điện trong mạch
- Khi mắc với một điện trở ngoài R = r
Cường độ dòng điện
\(I = \dfrac{E}{{R + r}} = \dfrac{E}{{r + r}} = \dfrac{E}{{2{\rm{r}}}}\)
- Khi thay nguồn bằng 3 nguồn điện giống hệt mắc song song: Eb = E
\({r_b} = \dfrac{r}{n} = \dfrac{r}{3}\)
Cường độ dòng điện khi này:
\(I' = \dfrac{{{E_b}}}{{R + {r_n}}} = \dfrac{E}{{r + \dfrac{r}{3}}} = \dfrac{{3E}}{{{\rm{4r}}}}\)
\(\dfrac{{I'}}{I} = \dfrac{3}{2} \to I' = 1,5I\)
Một bộ nguồn có ba nguồn giống nhau mắc nối tiếp. Mạch ngoài là một điện trở không đổi. Nếu đảo hai cực của một nguồn thì
- Khi 3 nguồn mắc nối tiếp: Eb = 3E, rb = 3r
\(I = \frac{{3E}}{{R + 3{\rm{r}}}}\)
- Khi đảo hai cực của một nguồn thì:
\({E_b}' = \left| {{E_1} - {E_2}} \right| + {E_3} = E,{r_b}' = 3{\rm{r,}}I' = \frac{E}{{R + 3{\rm{r}}}}\)
Hiệu điện thế giữa hai đầu điện trở mạch ngoài: UN = I.RN
Ta thấy cường độ dòng điện giảm 3 lần
=> Hiệu điện thế giữa hai đầu điện trở mạch ngoài giảm đi 3 lần
Một bộ nguồn có ba nguồn giống nhau mắc nối tiếp. Mạch ngoài là một điện trở không đổi. Nếu đảo hai cực của một nguồn thì
- Khi 3 nguồn mắc nối tiếp: Eb = 3E, rb = 3r
\(I = \frac{{3E}}{{R + 3{\rm{r}}}}\)
- Khi đảo hai cực của một nguồn thì:
\({E_b}' = \left| {{E_1} - {E_2}} \right| + {E_3} = E,{r_b}' = 3{\rm{r,}}I' = \frac{E}{{R + 3{\rm{r}}}}\)
Hiệu điện thế giữa hai đầu điện trở mạch ngoài: UN = I.RN
Ta thấy cường độ dòng điện giảm 3 lần
=> Hiệu điện thế giữa hai đầu điện trở mạch ngoài giảm đi 3 lần

