Câu hỏi:
2 năm trước
Có một số điện trở có \(r = 3\,\,\Omega \). Số điện trở \(r\) tối thiểu phải dùng để mắc thành mạch có điện trở \(5\,\,\left( \Omega \right)\) là:
Trả lời bởi giáo viên
Đáp án đúng: c
Do \({R_{td}} > r \to \) có ít nhất 1 điện trở \(r\) mắc nối tiếp với \({R_x}\)
Ta có: \({R_{td}} = r + {R_x} \Rightarrow {R_x} = {R_{td}} - r = 5 - 3 = 2\,\,\left( \Omega \right)\)
Ta thấy \({R_x} < r \to \) có ít nhất 1 điện trở \(r\) mắc song song với \({R_y}\)
Ta có: \(\frac{1}{{{R_x}}} = \frac{1}{r} + \frac{1}{{{R_y}}} \Rightarrow \frac{1}{2} = \frac{1}{3} + \frac{1}{{{R_y}}} \Rightarrow {R_y} = 6\,\,\left( \Omega \right)\)
Ta thấy \({R_y} = 6\Omega = 2r \to \) đoạn mạch \({R_y}\) gồm \(2\) điện trở \(r\) mắc nối tiếp
Ta có sơ đồ mạch điện:
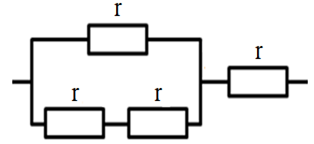
Vậy cần ít nhất \(4\) điện trở
Hướng dẫn giải:
Điện trở tương đương của đoạn mạch mắc nối tiếp:
\({R_{nt}} = {R_1} + {R_2} + ...\)
Điện trở tương đương của đoạn mạch mắc song song:
\(\frac{1}{{{R_{//}}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}} + ...\)
Câu hỏi khác
- Bài tập điện năng và công suất điện - định luật jun- lenxơ lý 11 có lời giải
- Bài tập định luật ôm đối với toàn mạch - mắc nguồn điện thành bộ lý 11 có lời giải
- Bài tập tính điện trở dây dẫn - biến trở có lời giải MÔN LÝ lớp 11
- Bài tập định luật ôm cho đoạn mạch chỉ có điện trở lý 11 có lời giải
- Bài tập đại cương về dòng điện không đổi - nguồn điện lý 11 có lời giải.
