Sợi quang trong cáp quang ứng dụng hiện tượng
Cáp quang là dây dẫn sáng ứng dụng phản xạ toàn phần để truyền tín hiệu trong thông tin và để nội soi trong y học
Một ống dẫn sáng hình trụ với lõi có chiết suất \({n_1} = 1,5\) và phần vỏ bọc ngoài có chiết suất\({n_2} = \sqrt 2 \). Chùm tia tới hội tụ tại mặt trước của ống tại điểm I với góc \(2\alpha \). Xác định \(\alpha \) lớn nhất để tia sáng trong chùm đều truyền được trong ống.
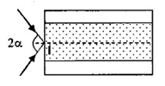
Tại I, ta có: \(1\sin \alpha = 1,5{\mathop{\rm s}\nolimits} {\rm{inr}}\) (1)
Để tia sáng truyền đi trong ống thì tại J phải xảy ra hiện tượng phản xạ toàn phần
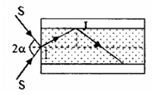
Ta có: góc tới tại J là: \({i_2} = {90^0} - r\)
Góc giới hạn tại J là: \(\sin {i_{gh}} = \frac{{n{}_2}}{{{n_1}}} = \frac{{\sqrt 2 }}{{1,5}} \to {i_{gh}} = 70,{53^0}\)
Điều kiện để xảy ra phản xạ toàn phần: \({i_J} \ge {i_{gh}} \leftrightarrow {90^0} - r \ge 70,{53^0} \to r \le 19,{47^0}\)
ta có, \({\alpha _{\max }} \Leftrightarrow {r_{\max }} = 19,{47^0}\)thay vào (1), ta được:
\(\sin {\alpha _{\max }} = 1,5{\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_{\max }} = 1,5.sin19,{47^0} \approx 0,5 \to {\alpha _{\max }} = {30^0}\)
Một tấm thủy tinh mỏng, trong suốt, chiết suất \({n_1} = 1,5\) có tiết diện là hình chữ nhật ABCD (AB rất lớn so với AD) mặt đáy AB tiếp xúc với một chất lỏng có chiết suất \({n_2} = \sqrt 2 \). Chiếu tia sáng SI nằm trong mặt phẳng ABCD tới mặt AD sao cho tia tới nằm phía trên pháp tuyến ở điểm tới và tia khúc xạ trong thủy tinh gặp đáy AB ở điểm K. Giá trị lớn nhất của góc tới i để có phản xạ toàn phần tại K.

Góc giới hạn phản xạ toàn phần: \(\sin {i_{gh}} = \frac{{{n_2}}}{{{n_1}}} = \frac{{\sqrt 2 }}{{1,5}} \to {i_{gh}} = 70,{53^0}\)
- Để tại K xảy ra hiện tượng phản xạ toàn phần thì: \({i_1} \ge {i_{gh}} = 70,{53^0}\)
\( \to {i_{{1_{\min }}}} = 70,{53^0}\)
Từ hình vẽ: \({r_{{\rm{max}}}} = {90^0} - {i_{{1_{\min }}}} = {90^0} - 70,{53^0} = 19,{47^0}\)
+ Áp dụng định luật khúc xạ ánh sáng tại I, ta có: \(1.\sin i = {n_1}{\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_{{\rm{max}}}} \to \sin {i_{{\rm{max}}}} = 1,5\sin (19,47) \approx 0,5 \to {i_{{\rm{max}}}} = {30^0}\)
Một khối thủy tinh hình bán cầu tâm O bán kính R, chiết suất \(n = \sqrt 2 \) đặt trong không khí. Chiếu một chùm tia sáng song song, rộng vào toàn bộ mặt phẳng của bán cầu và vuông góc với mặt phẳng đó.
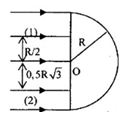
Vẽ tiếp đường đi của tia sáng (1) cách O đoạn R/2. Góc lệch của tia ló ra khỏi tấm thủy tinh so với tia tới là:
Ta có:
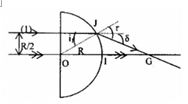
+ Góc giới hạn phản xạ toàn phần: \(\sin {i_{gh}} = \frac{1}{n} = \frac{1}{{\sqrt 2 }} \to {i_{gh}} = {45^0}\)
+ Tia (1) vuông góc với mặt phẳng nên truyền thẳng, đến mặt cầu dưới góc tới i
Từ hình, ta có: \(\sin i = \frac{{0,5R}}{R} = 0,5\)
Áp dụng định luật khúc xạ, ta có: \(n\sin {i_1} = {\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_1} \to {\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_1} = \frac{1}{{\sqrt 2 }} \to {r_1} = {45^0}\)
Góc lệch của tia ló so với tia tới: \(\Delta D = {r_1} - {i_1} = {45^0} - {30^0} = {15^0}\)
Kẻ trộm giấu viên kim cương ở dưới đáy một bể bơi. Anh ta đặt chiếc bè mỏng đồng chất hình tròn bán kính R trên mặt nước, tâm của bè nằm trên đường thẳng đứng đi qua viên kim cương. Mặt nước yên lặng và mức nước là h = 2,0m. Cho chiết suất của nước là \(n=\frac{4}{3}\). Giá trị nhỏ nhất của R để người ở ngoài bể bơi không nhìn thấy viên kim cương gần đúng bằng:
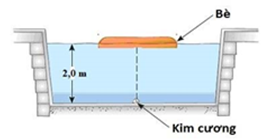
+ Để người ở ngoài bề không quan sát thấy viên kim cương thì tia sáng từ viên kim cương đến rìa của tấm bè bị phản xạ toàn phần, không cho tia khúc xạ ra ngoài không khí.
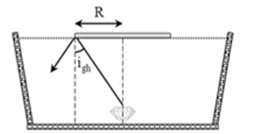
+ Góc tới giới hạn ứng với cặp môi trường nước và không khí:
\(\sin {{i}_{gh}}=\frac{{{n}_{2}}}{{{n}_{1}}}=\frac{1}{\frac{4}{3}}=\frac{3}{4}\Rightarrow {{i}_{gh}}={{48,6}^{0}}\)
+ Từ hình vẽ, ta có :
\(\tan {{i}_{gh}}=\frac{{{R}_{\min }}}{h}\Rightarrow {{R}_{\min }}=h.\tan {{i}_{gh}}=2.\tan {{48,6}^{0}}=2,27m\)
Cho 3 môi trường (1), (2), (3). Với cùng một góc tới, nếu ánh sáng đi từ (1) vào (2) thì góc khúc xạ là \({30^0}\), nếu ánh sáng đi từ (1) vào (3) thì góc khúc xạ là \({45^0}\). Hỏi môi trường (2) và (3) thì môi trường nào chiết quang hơn? Tính góc giới hạn phản xạ toàn phần giữa (2) và (3).
+ Áp dụng định luật khúc xạ ánh sáng cho môi trường tới 1 và môi trường khúc xạ 2, ta có:
\({n_1}\sin i = {n_2}{\mathop{\rm s}\nolimits} {\rm{in3}}{{\rm{0}}^0}\) (1)
+ Áp dụng định luật khúc xạ ánh sáng cho môi trường tới 1 và môi trường khúc xạ 3, ta có:
\({n_1}\sin i = {n_3}{\mathop{\rm s}\nolimits} {\rm{in4}}{{\rm{5}}^0}\)(2)
Từ (1) và (2), ta có: \({n_2}\sin {30^0} = {n_3}\sin {45^0} \to \dfrac{{{n_3}}}{{{n_2}}} = \dfrac{1}{{\sqrt 2 }} \to {n_2} > {n_3}\)
\( \Rightarrow \) (2) chiết quang hơn (3)
=> Góc giới hạn ở mặt phân cách giữa môi trường 2 và môi trường 3:
\(\sin {i_{gh}} = \dfrac{{{n_3}}}{{{n_2}}} = \dfrac{1}{{\sqrt 2 }} \to {i_{gh}} = {45^0}\)
Nước có chiết suất 1,33. Chiếu ánh sáng từ nước ra ngoài không khí, góc có thể xảy ra hiện tượng phản xạ toàn phần là
Điều kiện để xảy ra phản xạ toàn phần là:
\(\left\{ \begin{gathered}
{n_2} < {n_1} \hfill \\
i \geqslant {i_{gh}} \hfill \\
\end{gathered} \right.\)
Góc giới hạn phản xạ toàn phần được xác định bởi công thức :
\(\sin {i_{gh}} = \frac{{{n_2}}}{{{n_1}}} = \frac{1}{{1,33}} \Rightarrow {i_{gh}} = {48^0}45'\)
Chiếu một tia sáng đơn sắc từ không khí vào một chất lỏng trong suốt dưới góc tới 450 thì góc khúc xạ là 300. Bây giờ, chiếu tia sáng đó từ chất lỏng ra không khí dưới góc tới i. Với giá trị nào của i để có tia khúc xạ ra ngoài không khí?
+ Khi chiếu tia sáng từ không khí vào chất lỏng:
\(\sin {45^0}\; = n.\sin {30^0} \Rightarrow n = \dfrac{{\sin {{45}^0}}}{{\sin {{30}^0}}} = \sqrt 2 \)
+ Khi chiếu tia sáng từ chất lỏng ra không khí. Góc giới hạn phản xạ toàn phần là:
\(\sin {i_{gh}} = \dfrac{1}{n} = \dfrac{1}{{\sqrt 2 }} \Rightarrow {i_{gh}} = {45^0}\)
Để có góc khúc xạ thì không xảy ra hiện tượng phản xạ toàn phần nên \(i < {45^0}\)
Một chùm tia sáng hẹp SI truyền trong mặt phẳng tiết diện vuông góc của một khối trong suốt như hình vẽ. Tia sáng phản xạ toàn phần ở mặt AC. Trong điều kiện đó, chiết n của khối trong suốt có giá trị như thế nào?
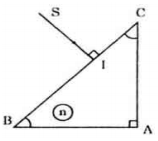
\(\Delta ABC\) vuông cân tại A \( \Rightarrow \widehat B = \widehat C = {45^0}\)
Có \(SI \bot BC \Rightarrow \)Tia SI truyền thẳng vào môi trường trong suốt ABC mà không bị khúc xạ
→ Góc tới ở I ở mặt khúc xạ AC: \(i = {45^0} \Rightarrow \sin i = \sin 45 = \dfrac{1}{{\sqrt 2 }}\)
Để tia sáng phản xạ toàn phần ở mặt AC thì:
\(i \ge {i_{gh}} \Leftrightarrow \sin i \ge \sin {i_{gh}} \Leftrightarrow \dfrac{1}{{\sqrt 2 }} \ge \dfrac{1}{n} \Rightarrow n \ge \sqrt 2 \)
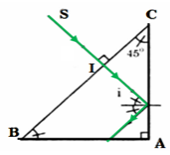
Một khối bán trụ trong suốt có chiết suất \(n = 1,41 \approx \sqrt 2 \). Một chùm tia sáng hẹp nằm trong mặt phẳng của tiết diện vuông góc, chiếu tới khối bán trụ như hình vẽ. Xác định góc khúc xạ ló ra ngoài không khí. Biết α = 300.
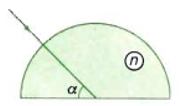

Ta có \(\alpha = {30^0} \Rightarrow i = {90^0} - \alpha = {60^0}\)
Góc giới hạn phản xạ toàn phần: \(\sin {i_{gh}} = \dfrac{1}{{\sqrt 2 }} \Rightarrow {i_{gh}} = {45^0}\)
Ta có: \(i = {60^0} > {i_{gh}}\)
→ Xảy ra hiện tượng phản xạ toàn phần.
Một sợi quang hình trụ gồm phần lõi có chiết suất n=1,58 và phần vỏ bọc có chiết suất no=1,41. Trong không khí, một tia sáng tới mặt trước của sợi quang tại điểm O (O nằm trên trục của sợi quang) với góc tới α rồi khúc xạ vào phần lõi (như hình bên). Để tia sáng chỉ truyền trong phần lõi thì giá trị lớn nhất của góc α gần nhất với giá trị nào sau đây?
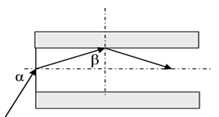
Ta có: \(\sin \left( {{i}_{gh}} \right)=\dfrac{{{n}_{0}}}{n}=\dfrac{1,41}{1,58}\Rightarrow {{i}_{gh}}=63,{{18}^{o}}\Rightarrow \beta \ge {{i}_{gh}}=63,{{18}^{o}}\)
\(\Rightarrow \) Góc khúc xạ tại mặt bên là \(r={{90}^{o}}-\beta \Rightarrow r\le 26,{{82}^{o}}\)
\(\sin \alpha =n\sin r\Rightarrow \alpha \le 45,{{48}^{o}}\approx {{45}^{o}}\)
Một ngọn đèn nhỏ \(S\) đặt ở đáy một bể nước \(\left( {n = \frac{4}{3}} \right)\), độ cao mực nước \(h = 60\,\,\left( {cm} \right)\). Bán kính \(r\) bé nhất của tấm gỗ tròn nổi trên mặt nước sao cho không một tia sáng nào từ \(S\) lọt ra ngoài không khí là:
Để không có tia sáng ra ngoài không khí, tia sáng bị phản xạ toàn phần tại mặt phân cách.
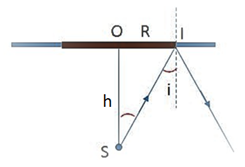
Để xảy ra hiện tượng phản xạ toàn phần, ta có:
\(\sin i \ge \sin {i_{gh}} \Rightarrow \sin i \ge \frac{1}{n}\)
Lại có: \(\sin i = \frac{r}{{\sqrt {{r^2} + {h^2}} }} = \frac{1}{{\sqrt {1 + \frac{{{h^2}}}{{{r^2}}}} }}\)
\(\begin{array}{l} \Rightarrow \frac{1}{{\sqrt {1 + \frac{{{h^2}}}{{{r^2}}}} }} \ge \frac{1}{n} \Rightarrow \sqrt {1 + \frac{{{h^2}}}{{{r^2}}}} \le n \Rightarrow 1 + \frac{{{h^2}}}{{{r^2}}} \le {n^2} \Rightarrow \frac{{{h^2}}}{{{r^2}}} \le {n^2} - 1\\ \Rightarrow \frac{h}{r} \le \sqrt {{n^2} - 1} \Rightarrow r \ge \frac{h}{{\sqrt {{n^2} - 1} }} \Rightarrow {r_{\min }} = \frac{h}{{\sqrt {{n^2} - 1} }} = \frac{{60}}{{\sqrt {{{\left( {\frac{4}{3}} \right)}^2} - 1} }} \approx 68\,\,\left( {cm} \right)\end{array}\)
Cáp quang dùng để truyền internet gồm có phần lõi và phần vỏ. Chiết suất của phần lõi và phần vỏ cần thỏa mãn điều kiện gì?
Cáp quang là bó sợi quang. Mỗi sợi quang là một dây trong suốt có tính dẫn sáng nhờ phản xạ toàn phần ở mặt phân cách giữa lõi và vỏ. Mà điều kiện xảy ra hiện tượng phản xạ toàn phần là ánh sáng truyền từ một môi trường tới môi trường chiết quang kém hơn.
Do đó sợi quang gồm hai phần chính là:
+ Phần lõi trong suốt bằng thuỷ tinh siêu sạch có chiết suất lớn \(\left( {{n_1}} \right).\)
+ Phần vỏ bọc cũng trong suốt, bằng thuỷ tinh có chiết suất \({n_2}\) nhỏ hơn phần lõi.
Trong các ứng dụng sau đây, ứng dụng của hiện tượng phản xạ toàn phần là:
Ứng dụng của hiện tượng phản xạ toàn phần cáp dẫn sáng trong nội soi.
Kẻ trộm giấu viên kim cương dưới đây một bể bơi, Anh ta đặt chiếc bè mỏng đồng chất hình tròn bán kính R trên mặt nước, tâm của bè nằm trên đường thẳng đứng đi qua viên kim vương. Mặt nước yên lặng và mức nước là 1,8m. Chiết suất của nước bằng 1,33. Giá trị nhỏ nhất của R để người ngoài bể bơi không nhìn thấy viên kim cương là:
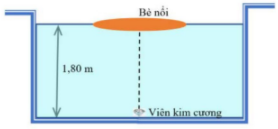
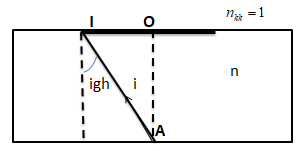
Để người ngoài bể bơi không quan sát thấy viên kim cương thì tia sáng từ viên kim cương đến mặt nước ngoài rìa của bè phải bị phản xạ toàn phần:
\(\sin {i_{gh}} = \frac{n}{{{n_{kk}}}} \Leftrightarrow \frac{R}{{\sqrt {{R^2} + 1,{8^2}} }} = \frac{1}{{1,33}}\)
\( \Leftrightarrow R = 2,05\left( m \right)\)

