Hiện tượng phản xạ toàn phần - Phương pháp giải bài tập phản xạ toàn phần

A – sai vì: phản xạ toàn phần xảy ra khi tia sáng đi từ môi trường có chiết suất lớn sang môi trường có chiết suất nhỏ hơn.

B – sai vì: khi truyền ánh sáng từ môi trường có chiết suất lướn sang môi trường chiết suất nhỏ hơn có thể xảy ra hiện tượng phản xạ toàn phần => không phải luôn có tia khúc xạ

C - đúng

D – sai vì: Khi có sự phản xạ toàn phần, cường độ sáng của chùm phản xạ gần như bằng cường độ sáng của chùm sáng tới.

Góc giới hạn được xác định bởi biểu thức: \(\sin {i_{gh}} = \dfrac{{{n_2}}}{{{n_1}}}\)

Ta có, điều kiện để xảy ra hiện tượng phản xạ toàn phần là ánh sáng phải truyền từ môi trường chiết quang hơn sang môi trường chiết quang kém (n₁ >  n₂)

=> Chọn D vì chiết suất của benzen > chiết suất của nước

=> Khi chiếu ánh sáng từ nước vào benzen sẽ chỉ xảy ra hiện tượng khúc xạ ánh sáng mà không xảy ra hiện tượng phản xạ toàn phần

Ta có, góc giới hạn được xác định:

\(\begin{array}{l}\sin {i_{gh}} = \dfrac{{{n_2}}}{{{n_1}}} = \dfrac{1}{{1,5}} = \dfrac{2}{3}\\ \to {i_{gh}} = 41,{8^0}\end{array}\)

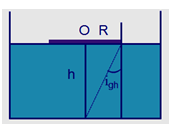
Ta có, góc giới hạn được xác định bởi biểu thức: \(\sin {i_{gh}} = \dfrac{{{n_2}}}{{{n_1}}} = \dfrac{1}{n}\)

Từ hình, ta có: \(\sin {i_{gh}} = \dfrac{R}{{\sqrt {{R^2} + {h^2}} }}\)

\(\begin{array}{l} \Rightarrow \dfrac{1}{n} = \dfrac{R}{{\sqrt {{R^2} + {h^2}} }}\\ \Leftrightarrow \dfrac{3}{4} = \dfrac{{10}}{{\sqrt {{{10}^2} + {h^2}} }}\\ \Rightarrow h = 8,82cm\end{array}\)

+ Áp dụng định luật khúc xạ ánh sáng cho môi trường tới 1 và môi trường khúc xạ 2, ta có:

\({n_1}\sin i = {n_2}{\mathop{\rm s}\nolimits} {\rm{in3}}{{\rm{0}}^0}\) (1)

+ Áp dụng định luật khúc xạ ánh sáng cho môi trường tới 1 và môi trường khúc xạ 3, ta có:

\({n_1}\sin i = {n_3}{\mathop{\rm s}\nolimits} {\rm{in6}}{{\rm{0}}^0}\)(2)

Từ (1) và (2), ta có:

\(\begin{array}{l}{n_2}\sin {30^0} = {n_3}\sin {60^0}\\ \Rightarrow \dfrac{{{n_3}}}{{{n_2}}} = \dfrac{1}{{\sqrt 3 }}\\ \Rightarrow {n_2} > {n_3}\end{array}\)

=> Góc giới hạn ở mặt phân cách giữa môi trường 2 và môi trường 3:

\(\begin{array}{l}\sin {i_{gh}} = \dfrac{{{n_3}}}{{{n_2}}} = \dfrac{1}{{\sqrt 3 }}\\ \Rightarrow {i_{gh}} = 35,{26^0}\end{array}\)

Phản xạ toàn phần là hiện tượng phản xạ toàn bộ tia sáng tới, xảy ra ở mặt phân cách giữa hai môi trường trong suốt.

Điều kiện đẻ xảy ra hiện tượng phản xạ toàn phần:

-  Ánh sáng truyền từ một môi trường tới môi trường chiết quang kém hơn : \({n_2} < {n_1}\)

- Góc tới lớn hơn hoặc bằng góc giới hạn:\(i \ge {i_{gh}}\)

A, B, C - đúng

D - sai vì: Sin góc giới hạn phản xạ toàn phần được xác định bằng tỉ số giữa chiết suất của môi trường kém chiết quang với môi trường chiết quang hơn chứ không phải góc giới hạn phản xạ toàn phần.

Khi xảy ra hiện tượng phản xạ toàn phần thì không còn tia khúc xạ (hay tia khúc xạ bị triệt tiêu) và cường độ của chùm tia phản xạ bằng cường độ chùm tia tới.

A, C, D - đúng

B- sai vì: khi truyền ánh sáng từ môi trường có chiết suất lướn sang môi trường chiết suất nhỏ hơn có thể xảy ra hiện tượng phản xạ toàn phần =>không phải luôn có tia khúc xạ

Góc giới hạn được xác định bởi biểu thức: \(\sin {i_{gh}} = \frac{{{n_2}}}{{{n_1}}}\)

Ta có, điều kiện để xảy ra hiện tượng phản xạ toàn phần là ánh sáng phải truyền từ môi trường chiết quang hơn sang môi trường chiết quang kém (n₁>  n₂)

=> Chọn A vì chiết suất của benzen > chiết suất của nước

Ta có, góc giới hạn được xác định: \(\sin {i_{gh}} = \dfrac{{{n_2}}}{{{n_1}}} = \dfrac{1}{{\dfrac{4}{3}}} = 0,75 \to {i_{gh}} = 48,{59^0}\)

Ta có:

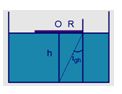
Ta có, góc giới hạn được xác định bởi biểu thức: \(\sin {i_{gh}} = \frac{{{n_2}}}{{{n_1}}} = \frac{1}{n}\)

Từ hình, ta có: \(\sin {i_{gh}} = \frac{R}{{\sqrt {{R^2} + {h^2}} }}\)

\( \to \frac{1}{n} = \frac{R}{{\sqrt {{R^2} + {h^2}} }} \leftrightarrow \frac{3}{4} = \frac{{20}}{{\sqrt {{{20}^2} + {h^2}} }} \to h = 17,64cm\)

- Cách 1:

Vì tia SI đi vuông góc với mặt AB nên đi thẳng tới mặt bên AC với góc tới i.

+ Tam giác ABC vuông và cân tại B nên: \(\widehat A = \widehat C = i = {45^0}\)

+ Tia ló đi là là mặt AC nên r = 90⁰

Theo định luật khúc xạ ánh sáng, ta có: \(n\sin {45^0} = 1.\sin {90^0} \to n = \sqrt 2 \)

- Cách 2:

Vì tia SI đi vuông góc với mặt AB nên đi thẳng tới mặt bên AC với góc tới i.

+ Tam giác ABC vuông và cân tại B nên: \(\widehat A = \widehat C = i = {45^0}\)

+ Tia ló đi là là mặt AC=>góc tới i chính là góc giới hạn:\(\sin {i_{gh}} = \frac{{{n_2}}}{{{n_1}}} \leftrightarrow \sin {45^0} = \frac{1}{n} \to n = \sqrt 2 \)

+ Áp dụng định luật khúc xạ ánh sáng cho môi trường tới 1 và môi trường khúc xạ 2, ta có:

\({n_1}\sin i = {n_2}{\mathop{\rm s}\nolimits} {\rm{in3}}{{\rm{0}}^0}\) (1)

+ Áp dụng định luật khúc xạ ánh sáng cho môi trường tới 1 và môi trường khúc xạ 3, ta có:

\({n_1}\sin i = {n_3}{\mathop{\rm s}\nolimits} {\rm{in4}}{{\rm{5}}^0}\)(2)

Từ (1) và (2), ta có: \({n_2}\sin {30^0} = {n_3}\sin {45^0} \to \frac{{{n_3}}}{{{n_2}}} = \frac{1}{{\sqrt 2 }} \to {n_2} > {n_3}\)

=> Góc giới hạn ở mặt phân cách giữa môi trường 2 và môi trường 3:

\(\sin {i_{gh}} = \frac{{{n_3}}}{{{n_2}}} = \frac{1}{{\sqrt 2 }} \to {i_{gh}} = {45^0}\)

Hướng dẫn giải:

Ta có:

+ Góc giới hạn phản xạ toàn phần: \(\sin {i_{gh}} = \frac{{{n_{kk}}}}{{{n_{nuoc}}}} = \frac{1}{{\frac{4}{3}}} = \frac{3}{4}\)

Gọi O - tâm đĩa tròn, càng xa O thì góc tới i càng tăng, để không có tia sáng nào lọt ra ngoài không khí thì ngay tại vị trí xa O nhất, tại đó vừa bắt đầu xảy ra hiện tượng phản xạ toàn phần.

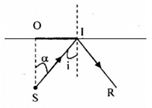
Ta có: 

\(\begin{array}{l}\alpha  = i = {i_{gh}}\\\sin \alpha  = \frac{{OI}}{{SI}} = \frac{{OI}}{{\sqrt {O{I^2} + O{S^2}} }} = \sin {i_{gh}} = \frac{3}{4}\\ \to O{S^2} = \frac{7}{9}{\rm{O}}{{\rm{I}}^2} \to {\rm{OS = }}\sqrt {\frac{7}{9}} OI = \sqrt {\frac{7}{9}} .5 = 4,41cm\end{array}\)

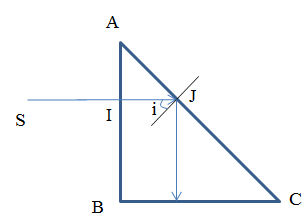
Tia SI đi đến mặt vuông góc với AB nên truyền thẳng đến mặt AC tại J với góc tới i.

∆ABC vuông cân tại B nên =>\(i = {45^0}\)

Góc giới hạn phản xạ toàn phần: \(\sin {i_{gh}} = \frac{{{n_{kk}}}}{n} = \frac{1}{{1,5}} \to {i_{gh}} = 41,{8^0}\)

nhận thấy \(i > {i_{gh}}\) =>tại J xảy ra hiện tượng phản xạ toàn phần với góc phản xạ 45⁰ => Tia phản xạ vuông góc với BC

=> Góc hợp bởi tia ló và tia tới là: \(D = {90^0}\)

Hiện tượng phản xạ toàn phần được ứng dụng làm cáp quang để để truyền tín hiệu trong thông tin và để nội soi trong y học