Câu hỏi:
2 năm trước
Một khối thủy tinh hình bán cầu tâm O bán kính R, chiết suất \(n = \sqrt 2 \) đặt trong không khí. Chiếu một chùm tia sáng song song, rộng vào toàn bộ mặt phẳng của bán cầu và vuông góc với mặt phẳng đó.
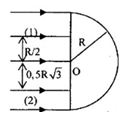
Vẽ tiếp đường đi của tia sáng (1) cách O đoạn R/2. Góc lệch của tia ló ra khỏi tấm thủy tinh so với tia tới là:
Trả lời bởi giáo viên
Đáp án đúng: c
Ta có:
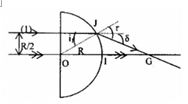
+ Góc giới hạn phản xạ toàn phần: \(\sin {i_{gh}} = \frac{1}{n} = \frac{1}{{\sqrt 2 }} \to {i_{gh}} = {45^0}\)
+ Tia (1) vuông góc với mặt phẳng nên truyền thẳng, đến mặt cầu dưới góc tới i
Từ hình, ta có: \(\sin i = \frac{{0,5R}}{R} = 0,5\)
Áp dụng định luật khúc xạ, ta có: \(n\sin {i_1} = {\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_1} \to {\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_1} = \frac{1}{{\sqrt 2 }} \to {r_1} = {45^0}\)
Góc lệch của tia ló so với tia tới: \(\Delta D = {r_1} - {i_1} = {45^0} - {30^0} = {15^0}\)
Hướng dẫn giải:
+ Vận dụng biểu thức tính góc giới hạn: \(\sin {i_{gh}} = \frac{{{n_2}}}{{{n_1}}}\)
+ Vận dụng biểu thức định luật khúc xạ ánh sáng: \({n_1}\sin i = {n_2}{\mathop{\rm s}\nolimits} {\rm{inr}}\)
