Câu hỏi:
2 năm trước
Một miếng gỗ hình tròn, bán kính \(R = 4cm\) . Ở tâm O, cắm thẳng góc một đinh OA. Thả miếng gỗ nổi trong một chậu nước có chiết suất \(n = 1,33\). Đỉnh OA ở trong nước. Tìm chiều dài lớn nhất của OA để mắt không thấy đầu A của đinh.
Trả lời bởi giáo viên
Đáp án đúng: a
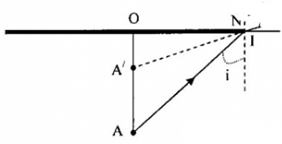
Để mắt không thấy đầu A của đinh thì góc tới \(i \ge {i_{gh}}\) vì lúc đó không có tia khúc xạ từ nước ra không khí.
Chiều dài lớn nhất của OA thỏa mãn điều kiện \(i = {i_{gh}}\) và đồng thời bị cạnh của miếng gỗ che lấp (như hình trên)
+ Ta có:
\(\begin{array}{l}\sin {i_{gh}} = \dfrac{{{n_2}}}{{{n_1}}} = \dfrac{1}{{1,33}} = 0,75\\ \Rightarrow {i_{gh}} = 48,{75^0}\end{array}\)
+ Từ hình, ta có:
\(\begin{array}{l}\tan i = \tan {i_{gh}} = \dfrac{{ON}}{{OA}}\\ \Rightarrow OA = \dfrac{{ON}}{{\tan {i_{gh}}}} = \dfrac{R}{{\tan 48,{{75}^0}}} = \dfrac{4}{{\tan 48,{{75}^0}}} = 3,5cm\end{array}\)
Hướng dẫn giải:
- Sử dụng hệ thức lượng giác trong tam giác
- Vận dụng biểu thức tính góc giới hạn: \(\sin {i_{gh}} = \dfrac{{{n_2}}}{{{n_1}}}\)
