Câu hỏi:
2 năm trước
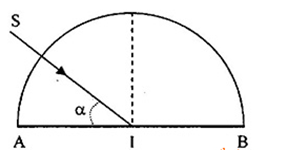
Một ống dẫn sáng hình trụ với lõi có chiết suất \({n_1} = 1,6\) và phần vỏ bọc ngoài có chiết suất\({n_2} = \sqrt 2 \). Chùm tia tới hội tụ tại mặt trước của ống tại điểm I với góc \(2\alpha \). Xác định \(\alpha \) lớn nhất để tia sáng trong chùm đều truyền được trong ống.
Trả lời bởi giáo viên
Đáp án đúng: c
Tại I, ta có: \(1\sin \alpha = 1,6{\mathop{\rm s}\nolimits} {\rm{inr}}\) (1)
Để tia sáng truyền đi trong ống thì tại J phải xảy ra hiện tượng phản xạ toàn phần
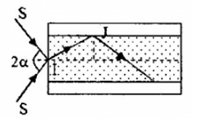
Ta có: góc tới tại J là: \({i_2} = {90^0} - r\)
Góc giới hạn tại J là: \(\sin {i_{gh}} = \dfrac{{n{}_2}}{{{n_1}}} = \dfrac{{\sqrt 2 }}{{1,6}} \to {i_{gh}} = 62,{11^0}\)
Điều kiện để xảy ra phản xạ toàn phần: \({i_J} \ge {i_{gh}} \leftrightarrow {90^0} - r \ge 62,{11^0} \to r \le 27,{89^0}\)
ta có, \({\alpha _{\max }} \Leftrightarrow {r_{ }} = 27,{89^0}\) thay vào (1), ta được:
\(\sin {\alpha _{\max }} = 1,6{\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_{ }} = 1,6.sin27,{89^0} \approx 0,75 \to {\alpha _{\max }} = 48,{6^0}\)
Hướng dẫn giải:
+ Vận dụng biểu thức định luật khúc xạ ánh sáng: \({n_1}\sin i = {n_2}{\mathop{\rm s}\nolimits} {\rm{inr}}\)
+ Vận dụng biểu thức tính góc giới hạn: \(\sin {i_{gh}} = \dfrac{{{n_2}}}{{{n_1}}}\)
+ Sử dụng điều kiện để xảy ra hiện tượng phản xạ toàn phần
