Cho mạch điện như hình vẽ. E =12 V ; r = 4Ω ; R1 =12Ω; R2 =24Ω ; R3= 8Ω. Cường độ dòng điện qua R1 và R3 là:
+) Ta có: \({R_3}nt\left( {{R_1}//{R_2}} \right)\)
\({R_{12}} = \dfrac{{{R_1}.{R_2}}}{{{R_1} + {R_2}}} = \dfrac{{12.24}}{{12 + 24}} = 8\Omega \)
\({R_N} = {R_{12}} + {R_3} = 8 + 8 = 16\Omega \)
Cường độ dòng điện trong toàn mạch là:
\(I = \dfrac{E}{{{R_N} + r}} = \dfrac{{12}}{{16 + 4}} = 0,6{\rm{A}}\)
+) Ta có: \(I = {I_3} = {I_{12}} = 0,6A\)
\({U_{12}} = {I_{12}}.{R_{12}} = 0,6.8 = 4,8V\)
\({R_1}//{R_2} \Rightarrow {U_{12}} = {U_1} = {U_2} = 4,8V\)
Suy ra: \({I_1} = \dfrac{{{U_1}}}{{{R_1}}} = \dfrac{{4,8}}{{12}} = 0,4A\)
Có một số điện trở có \(r = 3\,\,\Omega \). Số điện trở \(r\) tối thiểu phải dùng để mắc thành mạch có điện trở \(5\,\,\left( \Omega \right)\) là:
Do \({R_{td}} > r \to \) có ít nhất 1 điện trở \(r\) mắc nối tiếp với \({R_x}\)
Ta có: \({R_{td}} = r + {R_x} \Rightarrow {R_x} = {R_{td}} - r = 5 - 3 = 2\,\,\left( \Omega \right)\)
Ta thấy \({R_x} < r \to \) có ít nhất 1 điện trở \(r\) mắc song song với \({R_y}\)
Ta có: \(\frac{1}{{{R_x}}} = \frac{1}{r} + \frac{1}{{{R_y}}} \Rightarrow \frac{1}{2} = \frac{1}{3} + \frac{1}{{{R_y}}} \Rightarrow {R_y} = 6\,\,\left( \Omega \right)\)
Ta thấy \({R_y} = 6\Omega = 2r \to \) đoạn mạch \({R_y}\) gồm \(2\) điện trở \(r\) mắc nối tiếp
Ta có sơ đồ mạch điện:
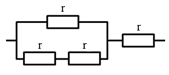
Vậy cần ít nhất \(4\) điện trở.
Có một số điện trở loại \(12\Omega \), phải dùng ít nhất bao nhiêu điện trở đó để mắc thành mạch có điện trở \(7,5\Omega \)
Ta có:
+ Vì \({R_{t{\rm{d}}}} = 7,5 < R\) nên có một điện trở mắc song song với Rx
Ta có: \(\dfrac{{12.{R_x}}}{{12 + {R_x}}} = 7,5 \Leftrightarrow {R_x} = 20\Omega \)
+ Vì Rx > R nên Rx gồm một điện trở R mắc nối tiếp với Ry.
Ta có: \({R_x} = R + {R_y} \Leftrightarrow {R_y} = 20 - 12 = 8\Omega \)
+ Vì Ry < R nên Ry gồm một điện trở R mắc song song với Rz
Ta có: \(\dfrac{{12.{R_z}}}{{12 + {R_z}}} = 8 \Leftrightarrow {R_z} = 24\Omega \)
+ Vì Rz > R nên Rz gồm một điện trở R mắc nối tiếp với Ra
Ta có: \({R_z} = R + {R_a} \Leftrightarrow {R_a} = 24 - 24 = 12\Omega = R\)
Vậy cần ít nhất 5 điện trở \(R = 12\Omega \) để mắc thành một đoạn mạch có điện trở tương đương là \(7,5\Omega \).
Một điện trở \({R_1}\) được mắc vào hai cực của một nguồn điện có điện trở trong \(r = 4\Omega \) thì dòng điện chạy trong mạch có cường độ là \({I_1} = 1,2A\). Nếu mắc thêm một điện trở \({R_2} = 2\Omega \) nối tiếp với điện trở \({R_1}\) thì dòng điện chạy trong mạch có cường độ là \({I_2} = 1A\). Trị số của điện trở \({R_1}\) là:
+ Ban đầu: \({I_1} = \dfrac{\xi }{{r + {R_1}}} \Leftrightarrow \dfrac{\xi }{{4 + {R_1}}} = 1,2A\,\,\left( 1 \right)\)
+ Mắc \({R_2}\,nt\,{R_1} \Rightarrow {R_N} = {R_1} + {R_2} = {R_1} + 2\)
\( \Rightarrow {I_2} = \dfrac{\xi }{{r + {R_N}}} \Leftrightarrow \dfrac{\xi }{{4 + {R_1} + 2}} = 1A\,\,\left( 2 \right)\)
+ Từ (1) và (2) ta có:
\(\begin{array}{l}1,2.\left( {4 + {R_1}} \right) = 1\left( {4 + {R_1} + 2} \right)\\ \Leftrightarrow 4,8 + 1,2{R_1} = 4 + {R_1} + 2 \Rightarrow {R_1} = 6\Omega \end{array}\)
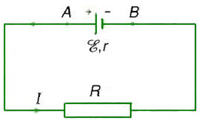
Xét mạch điện gồm điện trở được mắc vào hai đầu một bộ pin có điện trở trong như hình vẽ. Khi đó, cường độ dòng điện chạy trong mạch là 0,5 A. Suất điện động của bộ pin là:
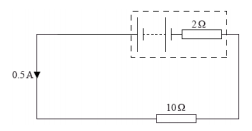
Ta có: \(I = \dfrac{E}{{R + r}}\)
\( \Rightarrow E = I.\left( {R + r} \right) = 0,5.\left( {10 + 2} \right) = 6V\)
Để xác định suất điện động E của một nguồn điện, một học sinh mắc mạch điện như hình bên (H1). Đóng khóa K và điều chỉnh con chạy C, kết quả đo được mô tả bởi đồ thị biểu diễn sự phụ thuộc của \(\dfrac{1}{I}\) (nghịch đảo số chỉ của ampe kế A) vào giá trị R của biến trở như hình bên (H2). Giá trị trung bình của E được xác định bởi thí nghiệm này là
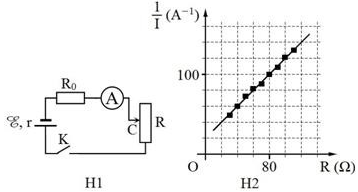
Từ đồ thị ta thấy có 2 cặp giá trị \(\left( {\dfrac{1}{I};R} \right)\) là (60; 40) và (100; 80)
Ta có công thức định luật Ôm:
\(I = \dfrac{E}{{R + {R_0} + r}} \Rightarrow \dfrac{1}{I} = \dfrac{{R + {R_0} + r}}{E}\)
Thay các cặp giá trị vào công thức, ta có:
\(\left\{ \begin{array}{l}60 = \dfrac{{40 + \left( {{R_0} + r} \right)}}{E}\\100 = \dfrac{{80 + \left( {{R_0} + r} \right)}}{E}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{R_0} + r = 20\,\,\left( \Omega \right)\\E = 1\,\,\left( V \right)\end{array} \right.\)
Người ta mắc hai cực nguồn điện không đổi với một biến trở. Điều chỉnh biến trở, đo hiệu điện thế \(U\) giữa hai cực của nguồn và dòng điện \(I\) chạy qua mạch ta vẽ lược đồ thị như hình vẽ. Xác định suất điện động và điện trở trong của nguồn.
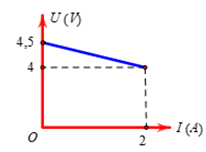
Điện áp giữa hai cực của nguồn là: \(U = \xi - I.r\)
Từ đồ thị ta có:
+ Khi \(\left\{ \begin{array}{l}U = 4,5V\\I = 0A\end{array} \right. \Rightarrow 4,5 = \xi - 0.r\,\,\,\left( 1 \right)\)
+ Khi \(\left\{ \begin{array}{l}U = 4V\\I = 2A\end{array} \right. \Rightarrow 4 = \xi - 2r\,\,\,\left( 2 \right)\)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{ \begin{array}{l}4,5 = \xi - 0.r\\4 = \xi - 2r\,\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\xi = 4,5V\\r = 0,25\Omega \end{array} \right.\)

