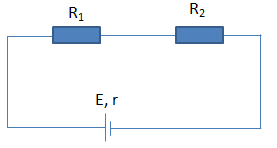
Một điện trở \({R_1}\) được mắc vào hai cực của một nguồn điện có điện trở trong \(r = 4\Omega \)  thì dòng điện chạy trong mạch có cường độ là \({I_1} = 1,2A\). Nếu mắc thêm một điện trở \({R_2} = 2\Omega \) nối tiếp với điện trở \({R_1}\) thì dòng điện chạy trong mạch có cường độ là \({I_2} = 1A\). Trị số của điện trở \({R_1}\) là:

Có \(x\)  nguồn giống nhau mắc nối tiếp, mỗi nguồn có suất điện động là \(3V\) điện trở trong là \(2\Omega \)  mắc với mạch ngoài là một bóng đèn loại \(\left( {6V - 6W} \right)\) thành một mạch kín. Để đèn sáng bình thường thì giá trị của \(x\)  là

Mắc điện trở \(R = 2\Omega \) vào bộ nguồn gồm hai pin có suất điện động và điện trở trong giống nhau. Nếu hai pin ghép nối tiếp thì cường độ dòng điện qua \(R\)  là \(I_1 = 0,75A.\) Nếu hai pin ghép song song thì cường độ dòng điện qua \(R\) là \(I_2 = 0,6A.\) Suất điện động và điện trở trong của mỗi pin có giá trị là

Để bóng đèn loại \(120V - 60W\) sáng bình thường ở mạng điện hiệu điện thế \(220\,\,V\) thì người ta phải mắc nối tiếp với bóng đèn một điện trở có giá trị

Trong một mạch kính gồm nguồn điện có suất điện động, điện trở ngang \(r\) và mạch ngoài có điện trở \(R\). Hệ thức nêu lên mối quan hệ giữa các đại lượng trên với cường độ dòng điện \(I\) chạy trong mạch là:

Cho mạch điện như sau:

Biết \({R_1} = {R_2} = r\). Cường độ dòng điện chạy trong mạch là:

Khi ghép nối tiếp các bộ nguồn với nhau ta được bộ nguồn có suất điện động

Khi ghép song song các bộ nguồn giống nhau với nhau ta được bộ nguồn có suất điện động