Hai điện tích \({q_1}\; = {2.10^{ - 8}}C;{q_2}\; = - {8.10^{ - 8}}C\)đặt tại A và B trong không khí; AB = 8cm. Một điện tích q3 đặt tại C. C ở đâu để q3 cân bằng.
Gọi \(\overrightarrow {{F_{13}}} ;\overrightarrow {{F_{23}}} \) lần lượt là lực do q1, q2 tác dụng lên q3
Để q3 cân bằng \( \Rightarrow \overrightarrow {{F_{13}}} + \overrightarrow {{F_{23}}} = 0 \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {{F_{13}}} \, \uparrow \downarrow \,\overrightarrow {{F_{23}}} \,\,\,\left( 1 \right)\\{F_{13}} = {F_{23}}\,\,\,\,\,\left( 2 \right)\end{array} \right.\)
Do \({q_1};{q_2}\) trái dấu → Để lực tổng hợp tại C bằng 0 thì C nằm ngoài AB và gần A hơn.
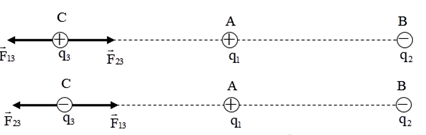
\( \Rightarrow CB - CA = AB = 8cm\,{\rm{ }}\left( 1 \right)\)
Lại có: \({F_{13}} = {F_{23}} \Leftrightarrow \dfrac{{k\left| {{q_1}{q_2}} \right|}}{{C{A^2}}} = \dfrac{{k\left| {{q_2}{q_3}} \right|}}{{C{B^2}}}\)
\( \Rightarrow \dfrac{{CA}}{{CB}} = \sqrt {\left| {\dfrac{{{q_1}}}{{{q_2}}}} \right|} = \dfrac{1}{2} \Rightarrow CB = 2.CA\,\,\,\left( 1 \right)\)
Từ (1) và (2) \( \Rightarrow \left\{ \begin{array}{l}CA = 8cm\\CB = 16cm\end{array} \right.\)
Hai điện tích \({q_1}\; = {8.10^{ - 8}}C;{q_2}\; = - {8.10^{ - 8}}\;C\)đặt tại A, B trong không khí (AB = 6 cm). Xác định lực tác dụng lên \({q_3}\; = {8.10^{ - 8}}C\) nếu: CA = 4cm, CB = 10cm
Điện tích q3 sẽ chịu hai lực tác dụng của q1 và q2 là:\(\overrightarrow {{F_1}} ;\overrightarrow {{F_2}} \)
Lực tổng hợp tác dụng lên q3 là: \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \)
Ta có: CA = 4cm, CB = 10cm
Vì CB – CA = AB nên C nằm trên đường AB, ngoài khoảng AB, về phía A.
Biểu diễn các lực tác dụng lên q3 ta có:
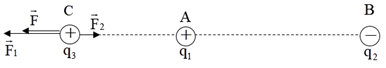
Từ hình vẽ ta thấy: \(\overrightarrow {{F_1}} \, \uparrow \downarrow \,\overrightarrow {{F_2}} \Rightarrow F = \left| {{F_1} - {F_2}} \right|\)
Với: \(\left\{ \begin{array}{l}{F_1} = \dfrac{{k.\left| {{q_1}{q_3}} \right|}}{{A{C^2}}} = \dfrac{{{{9.10}^9}.\left| {{{8.10}^{ - 8}}{{.8.10}^{ - 8}}} \right|}}{{0,{{04}^2}}} = {36.10^{ - 3}}N\\{F_2} = \dfrac{{k.\left| {{q_2}{q_3}} \right|}}{{B{C^2}}} = \dfrac{{{{9.10}^9}.\left| { - {{8.10}^{ - 8}}{{.8.10}^{ - 8}}} \right|}}{{0,{1^2}}} = 5,{76.10^{ - 3}}N\end{array} \right.\)
\( \Rightarrow F = \left| {{F_1} - {F_2}} \right| = \left| {{{36.10}^{ - 3}} - 5,{{76.10}^{ - 3}}} \right| = 30,{24.10^{ - 3}}N\)
Hai quả cầu nhỏ giống nhau bằng kim loại có khối lượng m = 5g, được treo vào cùng một điểm O bằng 2 sợi dây không dãn, dài 30cm. Tích điện cho mỗi quả cầu điện tích q như nhau thì thấy chúng đẩy nhau cho đến khi 2 dây treo hợp với nhau 1 góc 900. Tính điện tích mà ta đã truyền cho hai quả cầu. Lấy g = 10 (m/s2).
Khi quả cầu cân bằng thì: \(\overrightarrow P + \overrightarrow T + \overrightarrow {{F_d}} = 0\)
Đặt \(\overrightarrow {T'} = \overrightarrow P + \overrightarrow {{F_d}} \Rightarrow \overrightarrow {T'} + \overrightarrow T = 0 \Rightarrow \left\{ \begin{array}{l}\overrightarrow {T'} \, \uparrow \downarrow \overrightarrow T \\T' = T\end{array} \right.\)
Biểu diễn các lực tác dụng lên quả cầu:
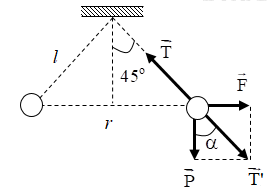
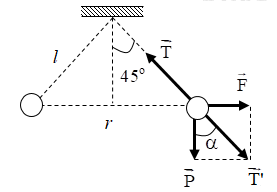
+ Từ hình vẽ ta có:
\(\begin{array}{l}\tan \alpha = \dfrac{{{F_d}}}{P} \Rightarrow {F_d} = P.\tan \alpha = mg.\tan \alpha \\ \Rightarrow {F_d} = {5.10^{ - 3}}.10.\tan 45 = 0,05N\end{array}\)
+ Mà: \(\left\{ \begin{array}{l}F = \dfrac{{k\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\\\left| {{q_1}} \right| = \left| {{q_1}} \right| = \left| q \right|\end{array} \right. \Rightarrow F = k.\dfrac{{{q^2}}}{{{r^2}}} \Rightarrow \left| q \right| = \sqrt {\dfrac{{F.{r^2}}}{k}} \)
+ Từ hình vẽ ta có: \(r = 2.\left( {l.\sin 45} \right) = l.\sqrt 2 \)
\( \Rightarrow \left| q \right| = \sqrt {\dfrac{{F.{{\left( {l\sqrt 2 } \right)}^2}}}{k}} = \sqrt {\dfrac{{0,05.{{\left( {0,3\sqrt 2 } \right)}^2}}}{{{{9.10}^9}}}} = {10^{ - 6}}C\)
+ Vậy tổng độ lớn điện tích đã truyền cho hai quả cầu là: \(Q = 2\left| q \right| = {2.10^{ - 6}}\;C\)
Cho hai điện tích q1 = 4µC, q2 > 0 nằm cố định tại hai điểm AB trong chân không như hình vẽ (b). Điện tích q3 = 0,6 µC nằm trên nửa đường thẳng Ax, hợp với AB góc 1500. Thay đổi vị trí của q3 trên Ax sao cho lực điện tổng hợp tác dụng lên điện tích q1 có độ lớn là 27 N đồng thời lực điện do q3 tác dụng lên q1 có giá trị cực đại. Khoảng cách giữa q3 và q1 lúc đó là
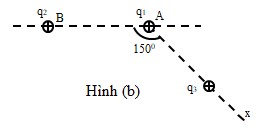
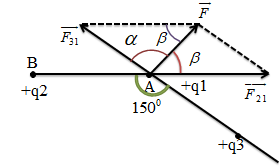
Biểu diễn các lực như hình vẽ.
Ta có:
\(\alpha + \beta = {150^0};{F_1} = 27N\)
Áp dụng định lý hàm sin cho tam giác F31AF21, ta có:
\(\dfrac{{{F_{31}}}}{{\sin \beta }} = \dfrac{{{F_1}}}{{\sin \left( {180 - \left( {\alpha + \beta } \right)} \right)}} = \dfrac{{{F_{21}}}}{{\sin \alpha }}\)
\( \Rightarrow {F_{31}} = \dfrac{{{F_1}\sin \beta }}{{\sin {{30}^0}}}\)
\({F_{31}}\max \) khi \(\sin \beta = {90^0}\). Khi đó:
\( \Rightarrow {F_{31}} = \dfrac{{{F_1}\sin {{90}^0}}}{{\sin {{30}^0}}} = \frac{{27.1}}{{0,5}} = 54N\)
Lại có:
\( \Rightarrow {F_{31}} = k\dfrac{{\left| {{q_1}{q_3}} \right|}}{{r_{13}^2}} = 54N\)
\(\begin{array}{l} \Leftrightarrow {9.10^9}.\dfrac{{{{4.10}^{ - 6}}.0,{{6.10}^{ - 6}}}}{{r_{13}^2}} = 54\\ \Leftrightarrow {r_{13}} = 0,02m = 2cm\end{array}\)
Hai điện tích điểm đặt trong không khí cách nhau 1m, đẩy nhau một lực F = 1,8N. Điện tích tổng cộng của hai vật là 3.10-5C. Tìm điện tích mỗi vật.
Ta có:
\(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}} \Leftrightarrow 1,8 = {9.10^9}.\dfrac{{\left| {{q_1}{q_2}} \right|}}{{{1^2}}} \Leftrightarrow \left| {{q_1}{q_2}} \right| = {2.10^{ - 10}}\) (1)
Lại có: \({q_1} + {q_2} = {3.10^{ - 5}}\) (2) => \({q_1} > 0;{q_2} > 0\)
Từ (1) và (2), suy ra:
\(\left\{ \begin{array}{l}{q_1} = {2.10^{ - 5}}C\\{q_2} = {1.10^{ - 5}}C\end{array} \right.\) hoặc \(\left\{ \begin{array}{l}{q_1} = {1.10^{ - 5}}C\\{q_2} = {2.10^{ - 5}}C\end{array} \right.\)

