Câu hỏi:
2 năm trước
Hai quả cầu nhỏ giống nhau bằng kim loại có khối lượng m = 5g, được treo vào cùng một điểm O bằng 2 sợi dây không dãn, dài 30cm. Tích điện cho mỗi quả cầu điện tích q như nhau thì thấy chúng đẩy nhau cho đến khi 2 dây treo hợp với nhau 1 góc 900. Tính điện tích mà ta đã truyền cho hai quả cầu. Lấy g = 10 (m/s2).
Trả lời bởi giáo viên
Đáp án đúng: b
Khi quả cầu cân bằng thì: \(\overrightarrow P + \overrightarrow T + \overrightarrow {{F_d}} = 0\)
Đặt \(\overrightarrow {T'} = \overrightarrow P + \overrightarrow {{F_d}} \Rightarrow \overrightarrow {T'} + \overrightarrow T = 0 \Rightarrow \left\{ \begin{array}{l}\overrightarrow {T'} \, \uparrow \downarrow \overrightarrow T \\T' = T\end{array} \right.\)
Biểu diễn các lực tác dụng lên quả cầu:
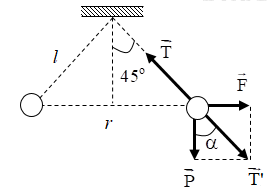
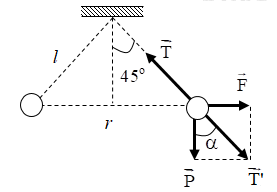
+ Từ hình vẽ ta có:
\(\begin{array}{l}\tan \alpha = \dfrac{{{F_d}}}{P} \Rightarrow {F_d} = P.\tan \alpha = mg.\tan \alpha \\ \Rightarrow {F_d} = {5.10^{ - 3}}.10.\tan 45 = 0,05N\end{array}\)
+ Mà: \(\left\{ \begin{array}{l}F = \dfrac{{k\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\\\left| {{q_1}} \right| = \left| {{q_1}} \right| = \left| q \right|\end{array} \right. \Rightarrow F = k.\dfrac{{{q^2}}}{{{r^2}}} \Rightarrow \left| q \right| = \sqrt {\dfrac{{F.{r^2}}}{k}} \)
+ Từ hình vẽ ta có: \(r = 2.\left( {l.\sin 45} \right) = l.\sqrt 2 \)
\( \Rightarrow \left| q \right| = \sqrt {\dfrac{{F.{{\left( {l\sqrt 2 } \right)}^2}}}{k}} = \sqrt {\dfrac{{0,05.{{\left( {0,3\sqrt 2 } \right)}^2}}}{{{{9.10}^9}}}} = {10^{ - 6}}C\)
+ Vậy tổng độ lớn điện tích đã truyền cho hai quả cầu là: \(Q = 2\left| q \right| = {2.10^{ - 6}}\;C\)
Hướng dẫn giải:
Định luật Cu – lông \(F = \dfrac{{k\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)
Điều kiện cân bằng: \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} + ... + \overrightarrow {{F_n}} = 0\)
Phân tích các lực tác dụng vào vật trên hình vẽ và sử dụng các kiến thức hình học.
