Cho hai điện tích điểm \({q_1} = {6.10^{ - 7}}C;{q_2} = - {8.10^{ - 7}}C\) đặt tại hai điểm A và B trong không khí cách nhau \(5cm.\) Xác định véc tơ cường độ điện trường tổng hợp tại M do \({q_1}\) và \({q_2}\) gây ra tại M biết \(MA = 3cm, MB = 8cm.\)
+ Cường độ điện trường do điện tích \({q_1}\) gây ra tại M:
\({E_1} = k\dfrac{{\left| {{q_1}} \right|}}{{A{M^2}}} = {9.10^9}\dfrac{{\left| {{{6.10}^{ - 7}}} \right|}}{{0,{{03}^2}}} = {60.10^5}V/m\)
+ Cường độ điện trường do điện tích \({q_2}\) gây ra tại M:
\({E_2} = k\dfrac{{\left| {{q_2}} \right|}}{{B{M^2}}} = {9.10^9}\dfrac{{\left| { - {{8.10}^{ - 7}}} \right|}}{{0,{{08}^2}}} = 11,{25.10^5}V/m\)
Cường độ điện trường tổng hợp tại M: \(\vec E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} {\rm{ }}\)
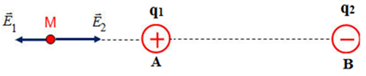
Từ hình vẽ ta có: \(\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \Rightarrow E = \left| {{E_1} - {E_2}} \right|\)
\( \Rightarrow E = \left| {{{60.10}^5} - 11,{{25.10}^5}} \right| = 48,{75.10^5}V/m\)
Một quả cầu kim loại nhỏ có khối lượng 1g được tích điện q = 10-5C treo vào đầu một sợi dây mảnh và đặt trong điện trường đều E. Khi quả cầu đứng cân bằng thì dây treo hợp với phương thẳng một góc 600, lấy g = 10m/s2. Tìm E.
Phân tích các lực tác dụng vào quả cầu ta có :
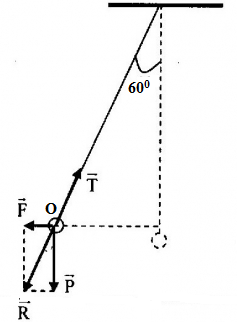
Từ hình vẽ ta có : \(\widehat {ROP} = {60^0}\)
Tam giác ROT vuông tại O, có :
\(\begin{array}{l}\tan \widehat {ROP} = \dfrac{F}{P} \Leftrightarrow \tan {60^0} = \dfrac{{\left| q \right|.E}}{{m.g}}\\ \Rightarrow E = \dfrac{{mg.\tan 60}}{{\left| q \right|}} = \dfrac{{{{10}^{ - 3}}.10.\tan 60}}{{{{10}^{ - 5}}}} = 1732V/m\end{array}\)
Cho hình vuông ABCD, tại A và C đặt các điện tích \(q_1 = q_3 = q = 2,5.10^{ - 8}C.\) Hỏi phải đặt tại B một điện tích bao nhiêu để cường độ điện trường tại D bằng \(0.\)
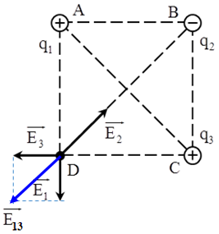
+ Cường độ điện trường tổng hợp tại D:\(\overrightarrow {{E_D}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + \overrightarrow {{E_3}} \)
Trong đó \(\overrightarrow {{E_1}} ;\overrightarrow {{E_2}} ;\overrightarrow {{E_3}} \) lần lượt là vecto cường độ điện trường do các điện tích \({q_1};{q_2};{q_3}\) gây ra tại D.
+ Vì \(\left\{\begin{matrix} q_1 = q_3 \\ AD = CD \end{matrix}\right. \Rightarrow E_1 = E_3 \Rightarrow E_{13} = \sqrt {2}E_1 = \sqrt {2}.\dfrac{k\left | q \right |}{a^2}\)
+ Ta có: \(\overrightarrow {{E_D}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + \overrightarrow {{E_3}} = \overrightarrow {{E_{13}}} + \overrightarrow {{E_2}} \)
Để cường độ điện trường tại O triệt tiêu thì:
\(\overrightarrow {{E_D}} = 0 \Leftrightarrow \overrightarrow {{E_{13}}} + \overrightarrow {{E_2}} = 0 \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {{E_{13}}} \uparrow \downarrow \overrightarrow {{E_2}} \,\,\left( 1 \right)\\{E_{13}} = {E_2}\,\,\,\,\,\left( 2 \right)\end{array} \right.\)
Từ (1) \( \Rightarrow \overrightarrow {{E_2}} \) hướng lại gần \({q_2} \Rightarrow {q_2} < 0\)
Từ (2) ta có:
\({E_2} = {E_{13}} \Leftrightarrow \dfrac{{k\left| {{q_2}} \right|}}{{{{\left( {a\sqrt 2 } \right)}^2}}} = \sqrt 2 .\dfrac{{k\left| q \right|}}{{{a^2}}} \Rightarrow \left| {{q_2}} \right| = 2\sqrt 2 .\left| q \right| = 2\sqrt 2 \left| q \right|\)
\(q_2 = - 2\sqrt{2}.2,5.10^{ - 8}C = - 5\sqrt{2}.10^{ - 8}C.\)
Bốn điểm A, B, C, D trong không khí tạo thành hình chữ nhật ABCD cạnh \(AD = a = 3cm;AB = b = 4cm\). Các điện tích \(q_1\,;\,q_2\,;\,q_3\)được đặt lần lượt tại A, B, C. Biết \(q_2 = - 12,5.10^{ - 8}C\) và cường độ điện trường tổng hợp tại D bằng \(0.\) Tính \({q_1};{q_2}\)?
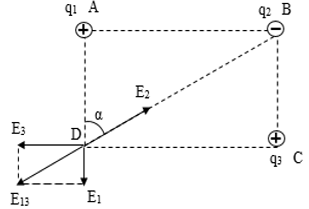
Vectơ cường độ điện trường tại D:
\(\overrightarrow {{E_D}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + \overrightarrow {{E_3}} = \overrightarrow {{E_{13}}} + \overrightarrow {{E_2}} \)
Do \(\overrightarrow {{E_D}} = 0 \Rightarrow \overrightarrow {{E_{13}}} + \overrightarrow {{E_2}} = 0 \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {{E_{13}}} \uparrow \downarrow \overrightarrow {{E_2}} \\{E_{13}} = {E_2}\end{array} \right.\)
Vì nên \({q_1};{q_3}\) phải là điện tích dương.
Từ hình vẽ ta có:
\(\begin{array}{l}{E_1} = {E_{13}}\cos \alpha = {E_2}.\cos \alpha \Leftrightarrow k.\dfrac{{\left| {{q_1}} \right|}}{{A{D^2}}} = k.\dfrac{{\left| {{q_2}} \right|}}{{B{D^2}}}.\dfrac{{AD}}{{BD}}\\ \Rightarrow \left| {{q_1}} \right| = \dfrac{{A{D^3}}}{{B{D^3}}}.\left| {{q_2}} \right| = \dfrac{{A{D^3}}}{{{{\left( {\sqrt {A{D^2} + A{B^2}} } \right)}^3}}}.\left| {{q_2}} \right|\\ \Rightarrow {q_1} = \dfrac{{{3^3}}}{{{{\left( {\sqrt {{3^2} + {4^2}} } \right)}^3}}}.12,{5.10^{ - 8}} = 2,{7.10^{ - 8}}C\end{array}\)
Tương tự ta có:
\(\begin{array}{l}{E_3} = {E_{13}}\sin \alpha = {E_2}.sin\alpha \Leftrightarrow k.\dfrac{{\left| {{q_3}} \right|}}{{A{B^2}}} = k.\dfrac{{\left| {{q_2}} \right|}}{{B{D^2}}}.\dfrac{{AB}}{{BD}}\\ \Rightarrow \left| {{q_3}} \right| = \dfrac{{A{B^3}}}{{B{D^3}}}.\left| {{q_2}} \right| = \dfrac{{A{B^3}}}{{{{\left( {\sqrt {A{D^2} + A{B^2}} } \right)}^3}}}.\left| {{q_2}} \right|\\ \Rightarrow {q_3} = \dfrac{{{4^3}}}{{{{\left( {\sqrt {{3^2} + {4^2}} } \right)}^3}}}.12,{5.10^{ - 8}} = 6,{4.10^{ - 8}}C\end{array}\)
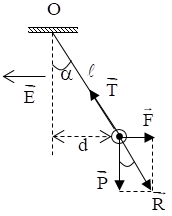
Một quả cầu khối lượng \(m = 4,{5.10^{ - 3}}kg\) treo vào một sợi dây dài \(2m.\) Quả cầu nằm trong điện trường có \(\overrightarrow E \) nằm ngang, hướng sang trái như hình vẽ. Biết \(d = 1m,E = 2000V/m\). Lấy \(g = 10{\rm{ }}m/{s^2}\).
Tính độ lớn của lực căng dây.
Lực tác dụng vào quả cầu: \(\overrightarrow P ;\overrightarrow {{F_d}} ;\overrightarrow T \)
Biểu diễn các lực tác dụng vào quả cầu như hình vẽ:
Khi quả cầu cân bằng: \(\overrightarrow P + \overrightarrow {{F_d}} + \overrightarrow T = 0\)
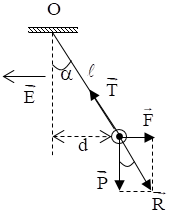
Đặt: \(\overrightarrow R = \overrightarrow P + \overrightarrow {{F_d}} \Rightarrow \overrightarrow T + \overrightarrow R = 0 \Rightarrow \left\{ \begin{array}{l}\overrightarrow T \uparrow \downarrow \overrightarrow R \\T = R\,\end{array} \right.\)
Từ hình vẽ ta có:
\(\cos \alpha = \dfrac{{\sqrt {{l^2} - {d^2}} }}{l} = \dfrac{P}{R} \Rightarrow R = P.\dfrac{l}{{\sqrt {{l^2} - {d^2}} }} = mg.\dfrac{l}{{\sqrt {{l^2} - {d^2}} }}\)
\( \Rightarrow R = 4,{5.10^{ - 3}}.10.\dfrac{2}{{\sqrt {{2^2} - {1^2}} }} = 0,052N\)
Vậy độ lớn lực căng dây: \(T = R = 0,052N\)
Một điện tích điểm \({q_1} = {4.10^{ - 6}}C\) đặt tại điểm A trong không khí.
Xác định độ lớn cường độ điện trường do q1 gây ra tại C cách A 10cm.
Độ lớn cường độ điện trường do q1 gây ra tại C là:
\({E_1} = k\dfrac{{\left| {{q_1}} \right|}}{{A{C^2}}} = {9.10^9}.\dfrac{{\left| {{{4.10}^{ - 6}}} \right|}}{{0,{1^2}}} = {36.10^5}V/m\)
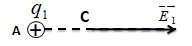
Một điện tích điểm \({q_1} = {4.10^{ - 6}}C\) đặt tại điểm A trong không khí.
Tại điểm B đặt thêm \({q_2} = - {16.10^{ - 6}}C\). Biết AB = 40 cm; BC = 30 cm. Xác định cường độ điện trường tổng hợp do q1 và q2 gây ra tại điểm C.
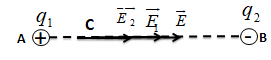
Ta có:
\({E_2} = k\frac{{\left| {{q_1}} \right|}}{{\varepsilon .B{C^2}}} = {9.10^9}.\frac{{\left| {{{16.10}^{ - 6}}} \right|}}{{0,{3^2}}} = {16.10^5}V/m\)
Cường độ điện trường tổng hợp do q1 và q2 gây ra tại C là:
\(\overrightarrow E = {\overrightarrow E _1} + {\overrightarrow E _2}\)
Có phương chiều được biểu diễn như hình vẽ.
Có độ lớn: \(E = {E_1} + {E_2} = {36.10^5} + {16.10^5} = {52.10^5}V/m\)
Tại một điểm trong không khí có hai cường độ điện trường có phương vuông góc với nhau và có độ lớn lần lượt là E1 = 6.104 V/m; E2 = 8.104 V/m. Độ lớn của điện trường tổng là:
Độ lớn điện trường tổng hợp là:
\(E = \sqrt {E_1^2 + E_2^2} = \sqrt {{{\left( {{{6.10}^4}} \right)}^2} + {{\left( {{{8.10}^4}} \right)}^2}} = {10.10^4}V/m\)
Một quả cầu nhỏ m = 0,25g, mang điện tích q = 5.10-9 C treo trên sợi dây mảnh trong điện trường đều có phương nằm ngang, cường độ điện trường E = 106V/m cho g = 10m/s2. Độ lớn lực điện trường tác dụng lên quả cầu là
Quả cầu chịu tác dụng của lực căng \(\overrightarrow T \), trọng lực \(\overrightarrow P \) và lực điện trường \(\overrightarrow F \).
Lực căng \(\overrightarrow T \) và trọng lực \(\overrightarrow P \) là hai lực cân bằng.
Suy ra, độ lớn lực điện trường tác dụng lên quả cầu là:
\(F = E.q = {10^6}{.5.10^{ - 9}} = {5.10^{ - 3}}N\)